6.2. Машинные алгоритмы вычисления определенных интегралов

Нередко бывает так, что воспользоваться формулой Ньютона-Лейбница для вычисления определенного интеграла не удается. Во-первых, получение аналитического выражения для F(x), когда оно существует, базируется на многочисленных приемах и ухищрениях. Замена переменной и интегрирование по частям – далеко не самые хитроумные из этих приемов. Освоить эти приемы и ухищрения – задача не из легких. Да и распознать по формуле f(x), какой из приемов для нее походит, тоже своего рода искусство. Поэтому часто усилия на получение аналитического выражения для F(x) оказываются чрезмерной платой за искомое число F. Во-вторых, далеко не каждая аналитически заданная функция f(x) имеет первообразную F(x) в форме аналитического выражения. Например, нет первообразной такой для функции f(x) . И, наконец, когда f(x) задана таблицей, взять интеграл аналитически от такой функции вообще невозможно. Поэтому для вычисления определенных интегралов применяют методы численного интегрирования. Эти методы универсальны и пригодны для любых f(x), (не только тогда, когда для f(x) нет F(x), но и тогда, когда можно было бы воспользоваться формулой Ньютона-Лейбница). На компьютерах методы численного интегрирования реализованы в виде стандартных программ.

Рассмотрим один из самых простых, но достаточно эффективных методов численного интегрирования – формулу трапеций.

Для численного интегрирования любую подынтегральную функцию f(x) на отрезке [a,b] задают таблицей {xt_i,yt_i}, у которой сетка axt₀,xt₁,...,xt_k,xt_k+1,...,xt_nb имеет достаточно малый шаг h , а yt_kf(xt_k) – отсчеты табличной функции (k ). К этой таблице применяют линейную аппроксимацию, а именно, на каждом интервале таблицы [xt_k,xt_k+1] длиною в h функцию f(x) заменяют прямой _k(x). Так вместо кривой f(x) получают ломаную линию (x){₀(x), ₁(x),, _k(x), _k1(x),, _n1(x)} (рис.6.3).

Далее, вместо того, чтобы вычислять площадь, ограниченную кривой f(x), вычисляют площадь, ограниченную ломаной (x). Для этого находят площади трапеции s₀, s₁,, s_k, s_k+1,, s_n-1:

s_k , k .

А потом все эти площади суммируют:

F_hs₀s₁s_ks_k+1s_n-2s_n-1

 

 .

Результатом суммирования и будет формула трапеций:

F_h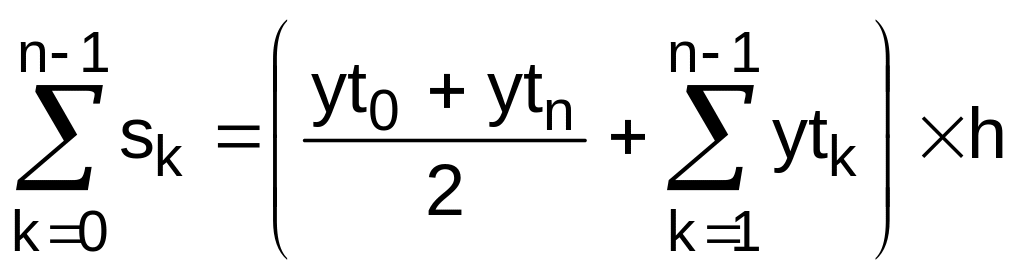 . (6.2)

Здесь F_h – значение определенного интеграла от функции f(x) по формуле трапеций на шаге h.

Достоинство формулы трапеций состоит в том, что процедура вычисления определенного интеграла не зависит от вида подынтегральной функции f(x), и сводится к простому суммированию отсчетов yt₀, yt₁,, yt_n табличной функции {xt_i,yt_i} с последующим умножением этой суммы на шаг таблицы h.

Если точным значением искомого интеграла будет величина F, то погрешность формулы трапеций на шаге h составит

R_hFF_hCh², (6.3)

где Cconst. Говорят, что формула трапеций имеет второй порядок точности (потому, что ее погрешность R_h пропорциональна h²). Повышают точность вычисления интеграла по формуле (6.2) путем уменьшения шага таблицы h (или, что то же самое, увеличением объема таблицы n). Второй порядок точности формулы трапеций означает, что уменьшение h вдвое снижает погрешность интегрирования в четыре раза. Однако пользоваться формулой (6.3) для оценки точности интегрирования неудобно. Дело в том, что здесь величина C не определена. Позже мы найдем более удобный способ оценивать погрешность численного интегрирования по формуле трапеций.

Допустим, что для заданной табличной функции {xt_i,yt_i} по формуле (6.2) получены: значение интеграла F_2h на шаге 2h и значение F_h на шаге h. Тогда, пользуясь формулой (6.3), можно составить следующую систему уравнений:

(6.4)

Исключив из этих уравнений неизвестное C, получим формулу Рунге-Ромберга для вычисления определенного интеграла:

FF_h .

Второе слагаемое в этой формуле

PR (6.5)

называют поправкой Рунге. Пользуясь этим обозначением, перепишем формулу Рунге-Ромберга:

FF_RRF_hPR. (6.6)

Здесь F_RR – значение определенного интеграла, вычисленное методом Рунге-Ромберга по формуле трапеций.

Формула (6.6) имеет четвертый порядок точности (уменьшение шага интегрирования вдвое уменьшает погрешность интегрирования в 2⁴16 раз). Достигается это за счет грамотного использования избыточной информации – результата интегрирования F_2h на шаге 2h (для вычисления поправки Рунге PR). Отметим интересный факт: когда f(x) – полином степени не выше третьей, формула Рунге-Ромберга дает точное значение определенного интеграла, хотя F_2h и F_h вычисляются по формуле трапеций с погрешностями.

Поправку Рунге можно использовать для оценки текущей точности интегрирования по формуле трапеций. В самом деле, вычтем первое уравнение из второго в системе (6.4):

F_hF_2hCh²3, Ch² .

Напомним, что величина Ch²FF_h характеризует погрешность формулы трапеций (6.2). Значит,

FF_h PR. (6.7)

Как видим, теперь в оценке погрешности интегрирования по формуле трапеций (6.2) нет нужды оперировать с неопределенной величиной C (см. формулу (6.3)), а использовать для этих целей текущее значение PR.

Итак, если вычисление определенного интеграла от заданной функции f(x) на заданном отрезке [a,b] по формуле Ньютона-Лейбница дает точный результат F_NL, то результат, полученный по формуле трапеций F_h, имеет в соответствии с (6.7) погрешность F_NLF_hPR.

Очевидно, что результат F_RR, полученный по методу Рунге-Ромберга должен отвечать неравенству

F_NLF_RRPR.

По окончании вычислений следует проверить это неравенство с тем, чтобы убедиться в верности полученных результатов.

Опишем процедуру вычисления определенного интеграла от таблично заданной функции {xt_i,yt_i} по формуле трапеций методом Рунге-Ромберга. Остановимся на том случае, когда таблица {xt_i,yt_i} составлена по результатам эксперимента. Значит, шаг такой таблицы уменьшить нельзя. Однако и от такой таблицы можно вычислить определенный интеграл с более высокой точностью, чем та, которую дает для нее формула трапеций (6.2). Делается это так. Сначала по формуле (6.2) вычисляют величину F_h, используя все отсчеты таблицы yt₀,yt₁,yt₂,...,yt_n, расстояние между которыми равно h. А затем вычисляют величину F_2h, используя только отсчетов таблицы yt₀,yt₂,...,yt_n c четными номерами, расстояние между которыми равно 2h. Имея значения F_h и F_2h, по формуле (6.5) вычисляют поправку Рунге PR, а потом по формуле (6.6) искомое значение определенного интеграла F_RR по методу Рунге-Ромберга, которое точнее чем F_h.

Для вычисления определенного интеграла методом Рунге-Ромберга объем n исходной таблицы {xt_i,yt_i} должен быть кратным степени двойки (см. (6.4)). Его минимальное значение n2 (рис. 6.4,а). Действительно, при таком объеме исходной таблицы на втором этапе вычислений (рис. 6.4,б) получим 1, и величина F_2h вычисляется как площадь одной трапеции, у которой основаниями будут только два крайних отсчета таблицы yt₀ и yt₁, а высота – суть 2hxt₁xt₀ba. Поэтому формулу (6.2) для метода Рунге-Ромберга следует преобразовать так:

F_h . (6.8)

На рис.6.5 показан граф алгоритма для вычисления определенного интеграла от таблично заданной функции по формуле трапеций методом Рунге-Ромберга. Здесь рис. 6.5,а описывает сам метод Рунге-Ромберга, а рис. 6.5,б задает вычисления по формуле трапеций (6.8). В блоке 0 (рис. 6.5,а) задаем табличную функцию {xt_i,yt_i}, ее объем n и шаг h. В блоке 1 из всех отсчетов {yt_i} табличной функции образуют массив Y. В блоке 2 происходит обращение к формуле трапеций (рис.6.5,б) с данными Y, n, h. Результатом будет значение F_h определенного интеграла на шаге h. В блоке 3 из отсчетов табличной функции с четными номерами формируем массив Y2, в котором эти отсчеты табличной функции получают новую сплошную нумерацию 0, 1, 2,..., . В блоке 4 массиву Y2 придаем имя Y, значение n уменьшаем, а шаг h увеличиваем вдвое. В боке 5 с этими новыми данными Y, n, h опять обращаемся к формуле трапеций (рис.6.5,б) и получаем величину F_2h, а именно, значение определенного интеграла на шаге 2h. В блоке 6 вычисляется поправка Рунге PR. Наконец, в блоке 7 получаем искомое значение F_RR определенного интеграла по формуле Рунге-Ромберга.

Пример. Выполним ручную прокрутку алгоритма (рис.6.5). В табл. 6.2 приведены данные о количестве преступлений в РФ за три года. Вычислить среднее количество преступлений за этот период.

Таблица 6.2
Зарегистрировано преступлений (тыс.)
i	0	1	2
Гтi	2005	2006	2007
Птi	3554.7	3855.4	3582.5
j	0		1

Действуем по рис.6.5,а, предварительно выполнив замену обозначений для операндов: xt_i, yt_i на Гт_i и Пт_i, Y, Y2 на П и П2, соответственно

0. Таблица {Гт_i,Пт_i} задана (табл. 6.2), объем n2, шаг h1.

1: П{3554.7, 3855.4, 3582.5}.

2: F_h  .

3: П2{3554.7, 3582.5}.

4: YY2, n1, h2.

5: F_2h  .

6: PR95.6.

7: F_RR7519.6.

Теперь вычислим среднее количество преступлений П_ср за период Г200720052 года.

П_ср  3759.8.

На рис. 6.6 представлены исходные данные и результаты решения задачи. Cветлыми кружками отмечены отсчеты табличной функции Пт_i, черными точками на оси абсцисс – значения Гт_i. На первом плане темной заливкой выделена трапеция площадью F_2h. На втором плане более светлой заливкой показаны две трапеции общей площадью F_h (их нижние части не видны). На заднем плане виден самый светлый прямоугольник площадью F_RR. Его высота равна искомой величине П_ср, а основание Г20072005.

Вопросы и задачи для самоконтроля

1. Сформулировать понятие определенного интеграла. Пояснить процедуру вычисления определенного интеграла по формуле Ньютона-Лейбница.

2. Определить понятие первообразной и неопределенного интеграла.

3. Перечислить свойства интегралов.

4. Записать таблицу интегралов.

5. Вычислить первообразные:

а) F(x) , б) F(x) ,

в) F(x) .

6. Вычислить площадь плоской фигуры, ограниченной параболой yx²1, на отрезке от a3 до b3.

7. Пояснить правила вычисления определенных интегралов методом замены переменной и по частям. Вычислить определенные интегралы:

а) F , б) F , в) F .

8. Пояснить, что такое несобственный интеграл. Вычислить

а) F , б) F .

9. Пояснить процедуру вывода формулы трапеций и смысл метода Рунге-Ромберга для вычисления определенных интегралов.

10. Вычислить для f(x)e^-x, a1.0, b3.0

а) по формуле Ньютона-Лейбница,

б) методом Рунге-Ромберга по формуле трапеций.

11. Выполнить ДКЗ: Тест 6. ОСНОВЫ ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ.

Эксцессом исполнителя признается совершение исполнителем преступления, не охватывающегося умыслом других соучастников. За эксцесс исполнителя другие соучастники преступления уголовной ответственности не подлежат.

(УК РФ, Ст. 36)