Глава 6. Основы интегрального исчисления

6.1. Определенный интеграл

К понятию определенного интеграла привели задачи вычисления обобщенных характеристик сложных процессов (скажем, таких как динамика преступности, безработицы и др.).

Пусть некоторый процесс y на отрезке [a,b] описывается функцией f(x). Обобщенной характеристикой этого процесса будет величина y_ср – среднее значение для y[f(a),f(b)]:

y_ср .

Здесь F – площадь криволинейной трапеции aABb (рис.6.1). Как видим, y_ср – суть высота прямоугольника aCDb, площадь которого тоже будет равна F.

Для определения y_ср нужно вычислить площадь F, которая ограничена кривой f(x) на отрезке [a,b]. Решение этой задачи описывается такой конструкцией:

F .

Правая часть этой записи читается так: определенный интеграл от a до b от f(x) по dx. Здесь:

f(x) – подынтегральная функция,

a – нижний предел интегрирования,

b – верхний предел интегрирования.

Итак, геометрический смысл определенного интеграла:

определенный интеграл от a до b от f(x) по dx – площадь, ограниченная кривой f(x) на отрезке [a,b].

Обычно для вычисления определенного интеграла пользуются формулой Ньютона-Лейбница:

FF_NL F(x) F(b)F(a), (6.1)

где F_NL – значение определенного интеграла F, полученное по формуле Ньютона-Лейбница,

F(x) –первообразная для подынтегральной функции f(x).

Функция F(x) называется первообразной для функции f(x), если f(x) получена как результат дифференцирования F(x):

f(x)F’(x).

Например, для f(x)3x² первообразной будет F(x)x³. В самом деле, (x³)’3x². Однако легко заметить, что и (x³1000)’3x², и (x³0.001)’3x², и вообще (x³C)’3x². Поэтому, если F(x) – первообразная для f(x), а C – любая константа, то и функция F(x)C также будет первообразной для f(x), то есть

f(x)(F(x)C)’. (6.2)

Вычисление первообразной F(x) для f(x) называют интегрированием функции f(x) и задают такой записью:

F(x).

Левая часть этой формулы читается так: неопределенный интеграл от f(x) по dx. Говорят, что для отыскания первообразной F(x) для f(x) нужно взять интеграл от функции f(x) или проинтегрировать функцию f(x).

Отметим, что Ньютон и Лейбниц практически в одно и то же время изобрели дифференциальное и интегральное исчисления. Однако юрист Лейбниц в отличие от физика Ньютона понимал важность эффективной математической символики, благодаря которой «поразительным образом сокращается работа мысли». Именно Лейбниц применил символ d для дифференциала и символ для интеграла.

Формулой (6.1) кодируют такую двухэтапную процедуру вычисления определенного интеграла.

Этап 1. Вычисляют неопределенный интеграл и находят выражение F(x) для первообразной.

Этап 2. В полученную формулу F(x) подставляют сначала xb и находят число F(b), потом в формулу F(x) подставляют xa и находят число F(a), а затем путем вычитания F(a) из F(b) находят искомое значение FF_NL.

В этой процедуре наибольшую сложность представляет этап 1. Поэтому остановимся подробно на методах вычисления неопределенных интегралов.

Отметим для начала, что в математике (строгости ради) результат вычисления первообразной записывают с учетом факта (6.2):

F(x)C

и константу C называют произвольной постоянной интегрирования. Подставим в формулу Ньютона-Лейбница вместо F(x) сумму F(x)C:

(F(x)C) (F(b)C)(F(a)C)F(b)F(a)F(x) .

Как видим, для наших целей отмеченная строгость не нужна, и результат вычисления неопределенного интеграла для использования его в формуле Ньютона-Лейбница достаточно представить только формулой F(x) (без слагаемого C).

При вычислении первообразной F(x) используют свойства интегралов, таблицы интегралов от типовых функций, те или иные приемы интегрирования.

Свойства интегралов. Сначала свойства неопределенных интегралов.

1. Неопределенный интеграл всегда берется от дифференциала искомой функции F(x):

  F(x).

2. Константу можно выносить за знак интеграла.

Пусть Aconst. Тогда

 .

3. Интеграл от суммы функций равен сумме интегралов от функций-слагаемых:

  .

Свойствами 2 и 3 обладают и определенные интегралы. Укажем еще два свойства определенных интегралов.

4. Если отрезок интегрирования [a,b] разбить на части, то интеграл по целому отрезку равен сумме интегралов по этим частным отрезкам:

  .

Иногда слагаемые в правой части этого равенства вычислить проще, чем его левую часть.

5. Перестановка пределов интегрирования равносильна изменению знака определенного интеграла:

 .

Действительно,

F(b)F(a)(F(a)F(b)) .

Значит, и

F(x) F(x) .

Таблица интегралов. В математике разработаны таблицы интегралов от тысяч функций. Мы же ограничимся таблицей интегралов от нескольких типовых функций (табл. 6.1).

Таблица 6.1
a)	0
b)	p1(!)
с)	при p1 ln(x), x0!
d)	
e)
f)
g)

Пример. Докажем верность формул в строках c) и d) табл. 6.1:

c) 

 

  

свойство 1 интеграловln(x).

d) 

 

  

свойство 1 интегралов .

Еще пример. Вычислим (рис.6.2) площадь, ограниченную кривой f(x)cos(x) на отрезке .

F .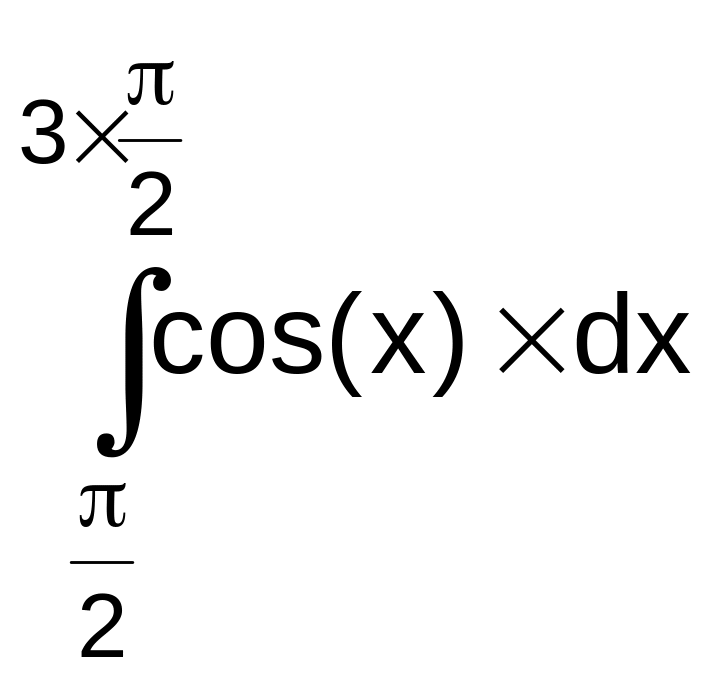

Этап 1.

F(x) .

Этап 2.

FF_NLsin(x)  2.

Этот пример иллюстрирует важную особенность определенного интеграла. В записи объекты x, f(x), dx, a, b – величины алгебраические, разность F(b)F(a) в формуле Ньютона-Лейбница тоже величина алгебраическая. Значит, и F_NL – алгебраическая величина (и, как в нашем примере, может принимать отрицательное значение).

В математике разработано огромное количество приемов интегрирования, которые применяются на первом этапе вычисления определенного интеграла и позволяют любой неопределенный интеграл преобразовать к табличному. Мы же опишем только два классических приема интегрирования.

Замена переменной. Этот прием применяется тогда, когда заданный интеграл имеет такой вид:

F ,

то есть под знаком интеграла стоит произведение сложной функции f((x)) на дифференциал вложенной функции ’(x)dx.

На первом этапе вычисления определенного интеграла F выполняют замену t(x). Тогда dtd(x)’(x)dx и

 F(t).

Для того чтобы формулу F(t) можно было бы использовать на втором этапе вычисления определенного интеграла, необходимо и пределы a и b по переменной x заменить пределами a_t и b_t по переменной t: a_t(a), b_t(b). Тогда

FF_NLF(t) F(b_t)F(a_t).

Пример. Вычислим

F .

Этап 1.

F(x) 

 

 



Этап 2.

FF_NL свойство 5 интегралов

   0.2.

Интегрирование по частям. Напомним формулу вычисления производной от произведения функций:

(u(x)v(x))’u’(x)v(x) u(x)v’(x).

Ясно, что первообразная для правой части этого равенства равна первообразной для его левой части:

u(x)v(x) .

Перепишем это равенство так:

.

В результате получили формулу интегрирования по частям. Ее можно записать более компактно, положив u(x)u, v(x)v, и :

.

Итак, если под знаком интеграла стоит произведение одной функции u на дифференциал dv от другой функции v, то, применив формулу интегрирования по частям, получим интеграл , который может оказаться табличным.

Пример. Вычислим

F .

Этап 1.

F(x) 

 

 .

Второй интеграл оказался не табличным и сложнее исходного . Значит, наш выбор u и dv оказался неудачным. Попробуем другой вариант назначения u и dv.

F(x) 

 

  .

Этап 2.

FF_NL(xcos(x)sin(x)) 

(cos()sin())(0cos(0)sin(0)).

Чтобы применить прием интегрирования по частям, нужно уметь разбить подынтегральное выражение на два множителя, а именно, на u и на dv. Никаких общих правил для этого нет, кроме следующих:

• dx должен быть всегда частью dv,

• нужно уметь брать интеграл от dv,

• когда интегрируемое выражение есть произведение двух функций, более сложную из них нужно рассматривать как часть дифференциала dv.

Во многих случаях один или оба предела интегрирования в определенном интеграле бесконечны. Интегралы с такими пределами относятся к несобственным интегралам. Операции взятия предела и интегрирования линейны: предел (интеграл) суммы равен сумме пределов (интегралов), а константу можно выносить за знак предела (интеграла). Поэтому определенный интеграл с бесконечным верхним пределом вычисляют так:

.

Пример. Вычислить несобственный интеграл

F .

Этап 1.

F(x) 

 

  .

Этап 2.

FF_NL  

1 1 !

Как видим, прямая подстановка b в выражение под знаком предела дает неопределенность вида . Рассмотрим эту ситуацию подробнее.

Если , то вычисление путем прямой подстановки приводит к неопределенности вида . Раскрывают эту неопределенность по правилу Лопиталя:

 !  .

Точно так записывается правило Лопиталя и для раскрытия неопределенности вида , когда

 !  .

Таким образом, правило Лопиталя состоит в том, что отношение функций под знаком предела заменяется отношением их производных , и уже в это новое отношение делают прямую подстановку.

Значит, в нашем случае

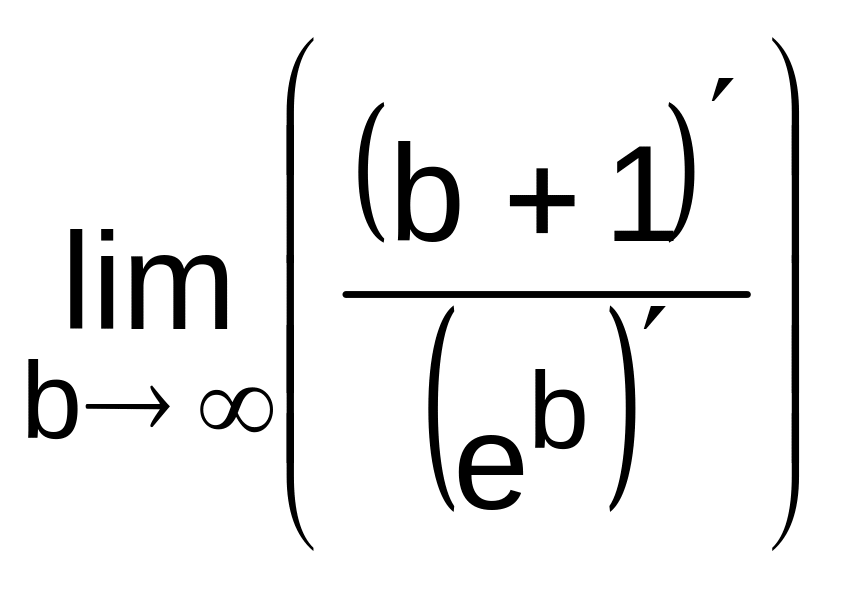
 !   0.

Итак,

FF_NL    

1 1 !1 101.

Аналогично вычисляют определенный интеграл с бесконечным нижним пределом:

,

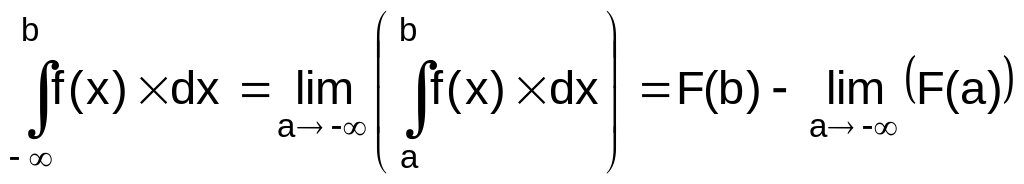с бесконечными верхним и нижним пределами интегрирования:

.