5.3. Дифференциал функции

Дифференциалы переменных x, y и др. обозначают как dx, dy и т.д. Определяются дифференциалы по-разному, в зависимости от того, является ли величина независимой переменной (аргументом) или функцией.

Дифференциал аргумента – это любое его приращение:

dxx.

Дифференциал функции yf(x) есть произведение ее производной f^’(x) на дифференциал независимой переменной dx:

dyf’(x)dx. (5.3)

Для дифференциала функции используют еще и такое обозначение:

d(f(x)).

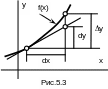
Рис.5.3 поясняет геометрический смысл дифференциала функции. Как видим, dy – это приращение, которое получает ордината касательной к f(x) в точке x при данном приращении аргумента dx. Говорят, что dy есть главная (линейная) часть приращения функции y. Это объясняется тем, что при малых dx приращение функции y почти совпадает с ее дифференциалом: ydy (рис.5.3).

Из определения дифференциала функции (5.3) получают еще и такие обозначения для ее производной:

f’(x) .

Правила вычисления производных задают и правила вычисления дифференциалов:

1. Если A,Bconst, то d(Af(x)Bg(x))Adf(x)Bdg(x).

2. Дифференциал произведения функций:

d(f(x)g(x))df(x)g(x) f(x)dg(x).

3. Дифференциал отношения функций:

.

Понятие дифференциала широко используется в приближенных вычислениях. Так, для определения погрешности функции y, обусловленной погрешностью ее аргумента x, пользуются формулой:

ydyf’(x)x. (5.4)

Вычислим, к примеру, погрешность S площади круга S, если его радиус r задается с точностью r.

Sr², SS(rr)², S2rrr².

А по формуле (5.4) получим:

S(r²)’r2rr.

Погрешность формулы (5.4) r² при малых r близка к нулю.

Так как дифференциал dy – основная часть приращения функции y, при малых x имеет место приближенное равенство dyy или же

f(xx)f(x)f’(x)x.

Отсюда

f(xx)f(x)f’(x)x. (5.5)

Полученная формула используется для приближенного вычисления нового значения функции f(xx), когда заданы ее старое значение f(x) и величина x.

Найдем, к примеру, значение . Положим, что здесь f(x) . Тогда f’(x) , xx16.64, x16, а x0.64. Значит, по формуле (5.5) получим:

f(xx)   x (1 ).

Теперь легко (практически в уме) вычислим

  21.012.02.

Вопросы и задачи для самоконтроля

1. Дать определение производной и пояснить ее геометрический смысл.

2. Найти производные функций:

а) y , б) y , в) y ,

г) ylog₂(x²), д) yarccos(x), е) yarctg(x).

3. Пояснить, как используется производная для исследования функций.

4. Исследовать функцию yx³3x²9x14 и построить ее график на отрезке [2,4].

5. Дать определение дифференциала функции и пояснить его геометрический смысл.

6. Записать дифференциалы функций:

а) y(x1)⁴, б) ysin²(x), в) y .

7. Пояснить, как используется дифференциал функции в приближенных вычислениях. Формула для вычисления погрешности функции из-за погрешности аргумента. Формула для вычисления нового значения функции по ее старому значению и приращению аргумента.

8. Вычислить приближенные значения величин:

а) , б) e^1.05, в) ln(e0.272), г) sin(24⁰).

9. Выполнить ДКЗ: Тест 5.ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ.