Глава 5. Основы дифференциального исчисления

5.1. Производная функции

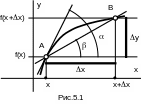
Пусть дана функция yf(x) (рис.5.1). Зафиксируем некоторую точку x из области определения D_f этой функции. А другая точка xx отстоит от x на величину x. Величина x называется приращением аргумента, а разность yf(xx)f(x) – приращением функции.

Производная функции yf(x) в точке x – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

. (5.1)

Поскольку yf(x), производную f^’(x) обозначают еще и как y’.

Процесс вычисления производной от функции f(x) называется ее дифференцированием.

Рис.5.1 поясняет геометрический смысл производной. Отношение есть тангенс угла  наклона секущей AB к оси 0x. Если теперь устремить x к нулю, то точка B на кривой f(x) станет приближаться к точке A, угол  устремится к значению . А  есть угол наклона касательной к кривой f(x) в точке A. Значит, производная от f(x) в точке x – это тангенс угла наклона (или угловой коэффициент) касательной к кривой f(x) в точке с абсциссой x:

f’(x)tg().

Производная имеет и физическое толкование, механический смысл. Исаак Ньютон нашел определение для мгновенной скорости тела, которое движется прямолинейно, но не равномерно (так, как двигался камень, отвесно брошенный Галилеем с вершины Пизанской башни). Пусть к моменту времени t тело прошло путь s(t), а к моменту tt – путь s(tt). Тогда средняя скорость тела на отрезке времени [t, tt] будет такой:

v_ср .

Если теперь устремить t к нулю, то пределом для v_ср и будет мгновенная скорость v(t) тела в момент времени t:

v(t) .

Значит, с физической точки зрения f’(x) – это мгновенная скорость изменения функции f(x) вблизи точки x.

Механический смысл производной иллюстрирует тот важный факт, что для функции yf(x), у которой y и x являются размерными величинами, размерность производной есть размерность y, деленная на размерность x (например, размерность скорости есть м/с или км/час).

Для произвольной точки xD_f производная f’(x) сама является функцией от x, и ее можно продифференцировать:

(f’(x))’f’’).

Получим производную от f(x) второго порядка – ускорение функции f(x) вблизи точки x. Вторая производная тоже есть функция от x. Продолжая этот процесс, найдем f⁽ⁿ⁾(x) – производную от f(x) n-го порядка. Если все n производных от f(x) существуют, то говорят, что f(x) дифференцируема n раз. Но для любого n

f⁽ⁿ⁾(x) ,

то есть производная f⁽ⁿ⁾(x) порядка n – это первая производная от производной (n1)-го порядка f^(n-1)(x), поэтому достаточно изучить подробно производную первого порядка f’(x).

Правила вычисления производной базируются на следующих свойствах производных (которые, в свою очередь, основаны на свойствах пределов, поскольку производная определена через предел).

1. Если C,Dconst, то

(Cf(x)Dg(x))’(Cf(x))’(Dg(x))’Cf’(x)Dg’(x)

(производная суммы есть сумма производных, константу можно выносить за знак производной).

2. Производная от произведения функций:

(f(x)g(x))’f’(x)g(x)f(x)g’(x).

3. Производная от отношения функций:

.

4. Производная сложной функции f(s(x))f(s):

(f(s(x)))’f’(s)s’(x) 

(производная сложной функции f(s) есть произведение производной внешней функции f по аргументу s на производную вложенной функции s по аргументу x).

5. Производная от обратной функции:

g’(x) .

Здесь предполагается, что f(x) – прямая функция, а g(x) – обратная, и производная от прямой функции f’(x) существует.

Все свойства доказываются с использованием определения производной (5.1) и уже доказанных ранее свойств. Докажем, к примеру, свойство 5, полагая, что все предыдущие свойства уже доказаны. Пусть прямая функция есть f(x), а обратная ей – функция g(x). Если они представлены в одной системе координат, то имеет место такое равенство:

f(g(x))x, (5.2)

(например, f(x)x², а g(x) , и f(g(x))( )²x).

Возьмем производные от левой и правой частей равенства (5.2). При этом левую часть дифференцируем с использованием правила 4:

f’(g(x))g’(x)1.

Отсюда

g’(x) .

Например, для f(x)x² и g(x) имеем:

f’(x) 2x,

значит,

Таблица 5.1
a)	(C)’0, Cconst
b)	(xp)’xp1p
c)	(ln(x))’ , x0!
d)	(loga(x))’
e)	(ex)’ex
f)	(ax)’axln(a)
g)	(sin(x))’cos(x)
h)	(cos(x))’sin(x)

( )’ .

В табл. 5.1 сведены производные от некоторых из элементарных функций. Эту таблицу и перечисленные выше свойства 1..5 используют при вычислении производных любых функций.

Пример. Доказать формулы d), e), f) в табл. 5.1, полагая, что остальные формулы доказаны:

d) (log_a(x))’  .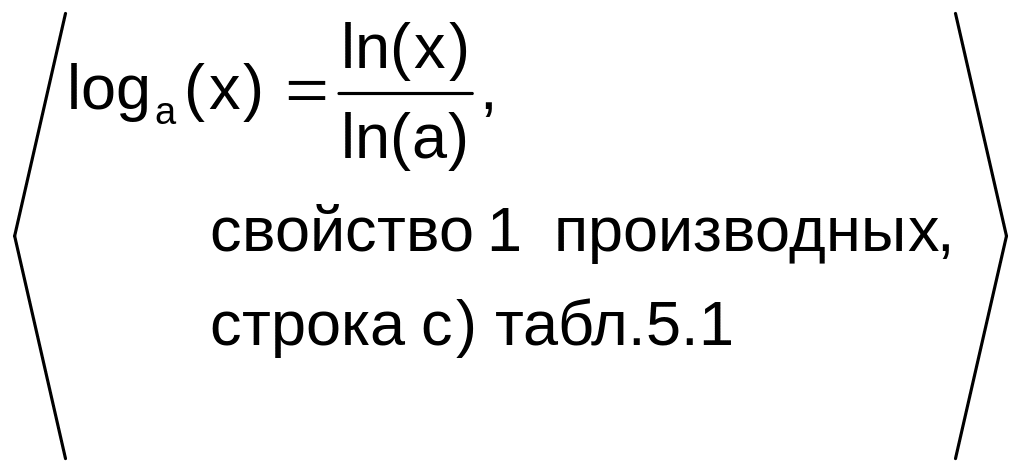

e) (e^x)’  e^x.

f) (a^x)’ a^xln(a).

Пример:

(e^-x)’ e^-x.