4.3. Предел функции

Отметим, что расстояние между числами p и q на числовой оси суть модуль разности этих чисел pq.

Зафиксируем на числовой оси точку a и положим, что переменная x меняется так, что каждое его следующее значение будет ближе к числу а, чем предыдущее. И какое бы малое число 0 ни назначить, настанет момент, когда будет выполнено условие xa, то есть расстояние от x до a будет меньше чем . И последующие изменения x никогда не нарушают это условие. Про такое поведение x говорят: x стремится к a, и этот факт обозначают конструкцией xa.

Число A называется пределом функции yf(x) при x, стремящемся к a, если для любого наперед заданного положительного  найдется такое положительное , что расстояние между y и A на оси ординат будет меньше чем , а расстояние между x и a на оси абсцисс будет меньше чем .

Записывается данное утверждение так:

.

Смысл этого определения поясняет рис.4.8. Как видим, значения функции yf(x) приближаются к числу A (расстояние yA уменьшается), когда значения аргумента x приближаются к a (расстояние xa уменьшается). Это означает, что для любого числа 0 наступит момент, когда будет выполняться неравенство yA. При этом можно назвать такое число 0, когда выполняется неравенство xa. Совместное выполнение этих неравенств и означает, что число A является пределом функции f(x) когда x стремится к a.

Тот факт, что число A является пределом функции f(x) при xa, устанавливают до того момента, когда расстояние xa окажется равным нулю, то есть x достигнет значения a. Поэтому в теории пределов вместо неравенства xa оперируют с системой неравенств 0xa.

Пример. Рассмотрим бесконечную последовательность точек на числовой оси xx₀, x₁, x₂,, x_k,:

x₀2 1, x₁2 1.5,

x₂2 1.75, …, x_k2 , …

Любое из этих чисел меньше a2. Но по мере роста значения k увеличивается и количество таких чисел, которые все теснее и теснее скапливаются около точки a2. Расстояние x_k2 уменьшается и с каждым новым k может стать меньше любого наперед заданного числа 0, то есть x2.

Каждому значению x из последовательности x₀, x₁,, x_k, отвечает свое значение функции yf(x). Например, значения функции yx² составят такую бесконечную последовательность:

y₀1²1, y₁1.5²2.25,

y₂1.75²3.0625, , y_k , 

Как видим, каждое следующее значение y_k все ближе к A4 и с каждым новым k разность y_k4 может стать меньше любого наперед заданного числа 0. Положим 2^30.13 и найдем . Из условия

y_k4  2^k22^3

находим, что неравенство y_k42^3 выполняется при k5.

Далее x_k2 2^k. При k5 получим, что x_k22^5. Значит, 2^50.03.

Таким образом, совместное выполнение неравенств y_k42^3 и 0x_k22^5 позволяет сделать вывод о том, что

.

И этот факт был установлен, несмотря на то, что равенство x_k2 не достигается ни при каком сколь угодно большом значении k.

Говорят, что x, если x меняется так, что каждое следующее его значение становится больше предыдущего. И какое бы большое положительное число M ни назначить, наступит момент, когда x окажется больше M, и далее это отношение между ними не меняется. Тогда утверждение означает следующее: для любого 0 найдется такое M0, чтоf(x)A при xM.

Говорят, что x, если x меняется так, что каждое следующее его значение становится меньше предыдущего. И какое бы большое положительное число M ни назначить, наступит момент, когда x окажется меньше M, и далее это отношение между ними не меняется. Тогда утверждение означает следующее: для любого 0 найдется такое M0, чтоf(x)A при xM.

Пусть имеются функции f(x) и g(x), которые имеют конечные пределы в точке xa (a – величина конечная или бесконечная):

, .

При вычислениях пределов используют следующие их свойства:

1) , Cconst.

2) .

3) .

4) .

5) , когда g(x)0 для axa, а B0.

Предложим читателю дать словесное толкование каждому из этих свойств.

Практически всегда при вычислении предела функции в первую очередь делают прямую подстановку xa в формулу для f(x) с тем, чтобы найти Af(a), то есть (см. рис. 4.8)

f(a)A.

Рассмотрим некоторые частные случаи.

• Имеем f(x) .

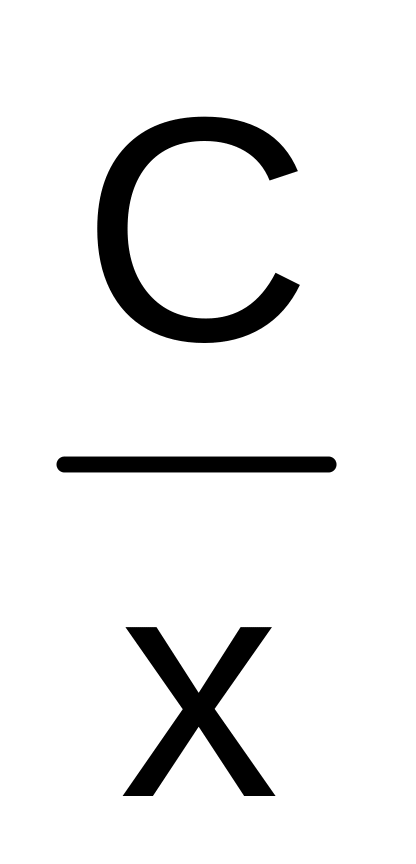Требуется вычислить .

Пусть , x0. Прямая подстановка x0 в f(x) дает результат f(0) ! Если же вычислять этот предел по определению, то картина будет такой: x0, то есть x неограниченно уменьшается, поэтому f(x) неограниченно возрастает, а именно, f(x). Значит, . Поэтому полученный ранее результат прямой подстановки толкуется так:

 !.

Если же , x0, то такие же рассуждения приводят к тому, что

 !.

Заметим, что делить нельзя на точный (!) нуль. А мы здесь и не делим на нуль.

Требуется вычислить .

В этом случае результат прямой подстановки толкуется так:

 !0.

• Пусть функции g(x) и h(x) таковы, что и , и . Требуется вычислить .

Прямая подстановка xa дает результат , который называют неопределенностью вида , поскольку и в числителе, и в знаменателе величины сколь угодно близкие к нулю, но не обязательно равные нулю. В этом случае нужно раскрыть неопределенность , а именно, выполнить преобразования выражений для g(x) и h(x), и вычислить предел от отношения результатов этого преобразования.

Положим, например, что g(x) и h(x) – полиномы степеней x:

g(x)a_nxⁿa_n-1x^n-1a₀, h(x)b_mx^mb_m-1x^m,-1b₀.

Тогда каждый из полиномов g(x) и h(x) следует разложить на множители. Один из этих множителей и в разложении g(x), и в разложении h(x) обязательно равен (xa). Поэтому числитель и знаменатель сократится на (xa). Результатом будет новая дробь , и остается вычислить предел прямой подстановкой.

Пример. Вычислим

 !

  5.

• Во многих случаях функция f(x) под знаком предела – рациональная дробь , у которой g(x) и h(x) – полиномы степеней x. Вычислим предел этой рациональной дроби при x:

 .

Прямая подстановка дает неопределенность вида . Раскрывают ее так: в числителе выносят за скобки xⁿ, а в знаменателе x^m:

  .

Первый из этих пределов вычисляют прямой подстановкой:

    .

А второй предел вычисляют по результатам анализа всех возможных отношений между n и m:

при nm получим nm0 и  0,

при nm получим nm0 и  1,

при nm получим nm0 и .

Изложенное позволяет найти искомый предел прямо по результатам анализа возможных отношений между n и m.

• При nm 0.

Например, n1, m2, nm0.

• При nm  .

Например, n2, m2, nm, a_n1, b_m2 .

• При nm .

Например, n3, m2, nm.

Вычислим предел рациональной дроби при x.

Укажем сразу, что

при nm и при nm вычисляется по тем же правилам, что и для x.

• А при nm для x получим





Например, n3, m2, nm, nm1, нечет..

В теории пределов обязательно рассматривают два предела, называемых замечательными:

• первый замечательный предел ,

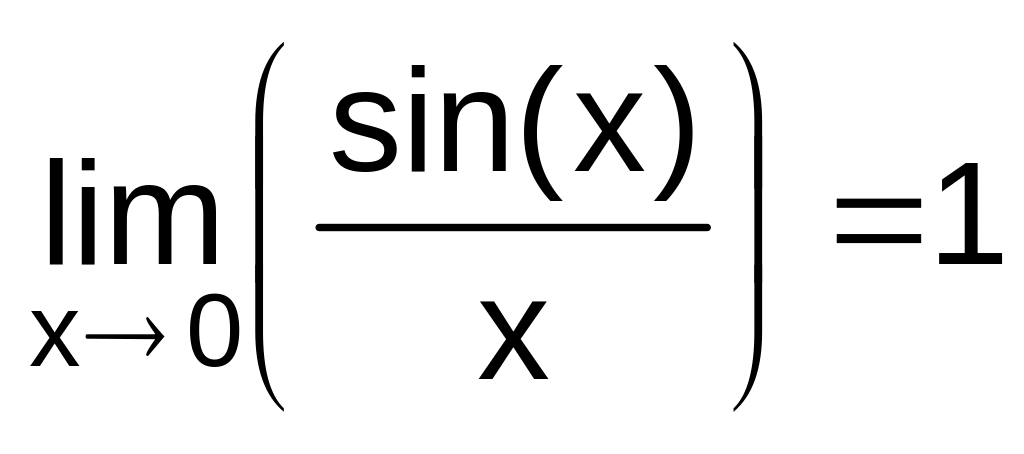• второй замечательный предел .

Внимание к этим пределам объясняется, в первую очередь, красотой и изяществом их доказательств (которые мы здесь, к сожалению, вынуждены опустить), а также тем, что с их помощью отыскиваются многие другие пределы.

Пример. Во времена расцвета в России финансовых пирамид концерн «Бетти» принимал вклады на три месяца под 100% (то есть обещал удвоить сумму вклада за три месяца). А при вкладе на 1.5 месяца ставка уменьшалась до 50%, при вкладе на три недели – до 25%, то есть при уменьшении срока вклада в n раз во столько же раз уменьшается и ставка. Отсюда следовало, что нужно положить деньги, скажем, на четверть срока, по истечении которого снять уже от вложенного, снова положить все деньги на четверть срока и т.д. Тогда за три месяца первоначальная сумма увеличится в 2.44 раза. Если же описанную процедуру повторять вдвое чаще, то сумма первоначального вклада за три месяца увеличится уже в 2.57 раза.

Найдем теоретический предел увеличения начального вклада. Последовательность , , наводит на мысль о том, что при разбиении трехмесячного срока на n частей получим . А теперь устремим n к бесконечности:

2.72.

Как видим, сложные проценты привели нас к числу e – основанию натуральных логарифмов.

Вопросы и задачи для самоконтроля

1. Определить понятие «функция». Какие бывают способы задания функций?

2. Построить графики функций:

а) ye^-x, x0; б) y1(x1)², y2x²1, xR.

3. Пояснить понятие «обратная функция». Как изобразить прямую и обратную функции в одной системе координат?

4. Найти функцию, обратную к y2^x. Построить графики прямой и обратной функций в одной системе координат.

5. Пояснить понятие «сложная функция».

6. Записать h(x)f(g(x)) для:

а) f(s) , sg(x)x²; б) f(s)e^s, sg(x)sin(x).

Построить графики каждой из сложных функций h(x).

7. Выделить вложенную и внешнюю функции

а) h(x) ; б) h(x) .

8. Пояснить смысл и назначение процедуры аппроксимации табличных функций. Привести формулы линейной аппроксимации табличной функции и пояснить процедуру их применения.

9. Зависимость количества D дорожных происшествий со смертельным исходом в год от числа v автомобилей на одну тысячу населения описывается соотношением вида

D(v) . (ДП)

Построить таблицу по формуле (ДП) на отрезке [a,b], a40, b200, n4.

Выполнить линейную аппроксимацию этой таблицы и найти значения D для v120, v2100 и v3240 по аппроксимирующим формулам.

Оценить погрешность аппроксимации.

10. Дать определение пределу функции. Пояснить вычисление предела путем прямой подстановки. Перечислить возможные результаты прямой подстановки.

11. Перечислить свойства пределов.

12. Пояснить, когда возникает и как раскрывается неопределенность вида .

13. Пояснить, как вычисляют предел от отношения полиномов при x, стремящемся к , к .

14. Записать определение для каждого из замечательных пределов.

15. Вычислить:

а) ; б) ; в) ;

г) ; д) ; е) .

16. Выполнить ДКЗ: Тест 4. ФУНКЦИИ.