Раздел II основы математического анализа Глава 4. Функции

4.1. Понятие функции

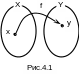Пусть X и Y – непустые числовые множества (рис.4.1).

Функцией из X в Y называют закон f, по которому каждому элементу xX ставится в соответствие единственный элемент yY.

Элемент xX называют аргументом, а элемент yY – значением функции f. Множество X называется областью определения функции f (областью ее существования), а множество Y – областью значений функции f. Область определения и область значений функции f обозначим как D_f и E_f, соответственно.

Задать функцию – значит указать область ее определения D_f, область ее значений E_f и сформулировать закон (правило) f о том, как для каждого заданного x получить свой y.

Известны следующие способы задания функций:

• аналитический,

• табличный,

• графический.

Задать функцию аналитически – это записать ее формулой. Если множества X и Y определены, то функцию из X в Y задают записью вида yf(x). Это наиболее компактный, удобный и универсальный способ задания функции. Формулой задают набор вычислительных операций над x, выполнив которые получают y. Обычно по формуле можно найти и область определения функции, и область ее значений. Когда мы читаем запись

y0.25x³, (4.1)

нам ясно, что эта функция ставит в соответствие каждому числу x четвертую часть его куба. Эта функция определена на всей числовой оси: xR, и область ее значений – тоже множество вещественных чисел yR.

Конечно, для обозначения самой функции, ее аргумента и ее значений кроме букв f, x, y можно применить любые другие буквы, а может быть и их сочетания (если не пропускать, как это мы и делаем, знак  умножения в записях произведений).

Табличный способ задать функцию состоит в том, что значения аргумента записывают в одной строке (в одном столбце), а значения функции – в другой строке (в другом столбце). Правило f здесь предельно простое: под каждым (рядом с каждым) значением табличного аргумента xt_i – свое значение табличной функции yt_i.

Таблицу можно построить по аналитическому выражению функции. Часто в таблицу сводят результаты эксперимента, каждый из которых не имеет соответствующего аналитического описания.

Если функция задана аналитически, то процедура построения ее таблицы состоит в следующем.

Область определения функции ограничивают отрезком [a,b]. На этом отрезке задают сетку

axt₀,xt₁,xt₂,,xt_i,xt_i+1,,xt_nb

с равномерным шагом h , где n – объем таблицы. Понятно, что xt_iaih, i . Это содержимое первой строки будущей таблицы.

Для каждого значения xt_i по формуле yt_if(xt_i) вычисляют отсчеты табличной функции. Так получают вторую строку таблицы. Удобно бывает дополнить таблицу еще одной (верхней) строкой с номерами 0, 1,…, i, i1,…, n ее отсчетов.

Пример. Построим таблицу по аналитическому выражению (4.1).

Ограничимся отрезком [0,2] и n4. Имеем:

h 0.5, xt_iaih, yt_i0.25(xt_i)³.

В результате получим табл.4.1.

Таблица 4.1
i	0	1	2	3	4
xti	0.0	0.5	1.0	1.5	2.0
yti	0.00	0.03	0.25	0.84	2.00

Таблично заданную функцию будем представлять такой конструкцией: {xt_i,yt_i}.

Аналитический и табличный способы задания функции недостаточно наглядны. Это обусловливает применение графического способа задания функции. Обычно график дополняет другие способы задания функции. Строится график всегда по таблице чаще всего в декартовых координатах. Декартова система координат образована двумя взаимно перпендикулярными прямыми. Горизонтальная прямая – это ось абсцисс 0x, вертикальная прямая – ось ординат 0y. Точка пересечения осей служит началом координат. По каждой из осей задают шкалу. Цена делений по оси 0x равна или кратна шагу таблицы h. Цену делений по оси 0y вычисляют по данным во второй строке таблицы так, чтобы получить удобочитаемые числа по оси 0y.

Итак, сначала строится таблица {xt_i,yt_i}. По данным этой таблицы строится точечный график. Каждой паре чисел xt_i и yt_i из колонки таблицы номер i на координатной плоскости ставят в соответствие точку (xt_i,yt_i). Эти точки на графике соединяют плавной кривой.

На рис.4.2 показан график, построенный по табл. 4.1. Здесь кружочками показаны точки табличной функции, и они соединены плавной линией.

В данном разделе мы ограничим наши интересы только такими функциями, каждая из которых не имеет особенностей в области ее определения.

Обратная функция. Пусть функция f имеет для y ровно столько же разных значений, сколько значений имеет и ее аргумент x. Отсюда следует, что уравнение f(x)y всегда можно разрешить относительно x и записать xg(y).

Функция g, которая ставит в соответствие каждому элементу yY единственный элемент xX, такой, что y f(x), называется обратной к функции f (рис.4.3).

Функцию f называют прямой (исходной). Область определения обратной функции совпадает с областью значений исходной функции и наоборот . Функция, обратная к g, есть прямая функция f. Значит, функции f и g – взаимно обратные.

Пример. Пусть исходная функция y2^x. Построим ее график. Для этого составим табл.4.2, построим точечный график и соединим точки, заданные таблицей, плавной линией (рис.4.4). Как видим, эта функция возрастает на всей числовой оси и ограничена снизу осью абсцисс.

	Таблица 4.2
f(x)	x	3	2	1	0	1	2	y		g(x)
	y				1	2	4	x

А теперь найдем функцию, обратную к y2^x, и построим ее график в тех же (!) координатах, что и график прямой функции. Для этого в записи исходной функции поменяем местами x и y: x2^y. Из этого уравнения найдем y: ylog₂(x). Это и есть функция, обратная к исходной y2^x. Таблицу обратной функции получают из таблицы исходной, поменяв в ней местами обозначения строк (табл. 4.2). По этой таблице и строим график обратной функции (рис.4.4). Как видим, это функция – возрастающая при x0, и она не ограничена.

Данный пример иллюстрирует общее свойство взаимно обратных функций: графики исходной и обратной функций имеют осью симметрии прямую yx (когда масштабы по осям координат одинаковы).

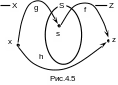
Сложная функция. Пусть заданы функции sg(x) и zf(s) такие, что область определения функции f совпадает с областью значений функции g (рис.4.5). Функция g отображает множество X на множество S, а функция f отображает множество S на множество Z. Эти два отображения вместе задают новое отображение h множества X на множество Z. Такое отображение и называется сложной функцией (суперпозицией функций f и g):

zf(g(x))h(x).

Например,

sg(x)sin(x), f(s)s².

Тогда

zf(g(x))(sin(x))²h(x).

Если же

sg(x)x², а f(s)sin(s),

то

zf(g(x))sin(x²)h(x).

В суперпозиции функций f(g(x)) функцию sg(x) называют вложенной, а функцию f(s) называют внешней.

На практике проблема состоит в том, что заданной является функция h(x), а нужно бывает найти и выделить вложенную и внешнюю функции. Для этого поступают так. Мысленно задают значение аргумента x и фиксируют те действия в h(x), которые выполняются над ним в первую очередь. Эти действия и образуют вложенную функцию sg(x). Далее определяют те действия в h(x), которые производятся над s – результатом вложенной функции. Они и составляют внешнюю функцию zf(s).

Например, имеем

h(x) .

Здесь в первую очередь x возводят в куб, а из полученного результата извлекают корень пятой степени, значит,

sg(x)x³, zf(s) .

Можно составить суперпозицию из трех и более функций. Например,

h(x) . sx³, z , v .