Характеристика точности моделей
После получения оценки параметров нескольких моделей, адекватно отражающих реальный процесс порождения данных, определяется точность выбранной модели. Выбор основывается на сравнении показателей абсолютной ошибки, средней относительной ошибки и среднеквадратической ошибки.
В ходе данной работы была определена точность параметров рядов динамики линейной и параболической, аддитивной моделей.
Средняя
абсолютная ошибка определяется по
формуле
.
Средняя
относительная ошибка определяется по
формуле
.
Среднеквадратическая
ошибка рассчитывается по формуле
.
Определяется ошибки линейной модели по исходному временному ряду.
Была
построена линейная модель по уравнению
.
Далее рассчитаны ошибки. Результаты
показаны на рисунке 10.1.
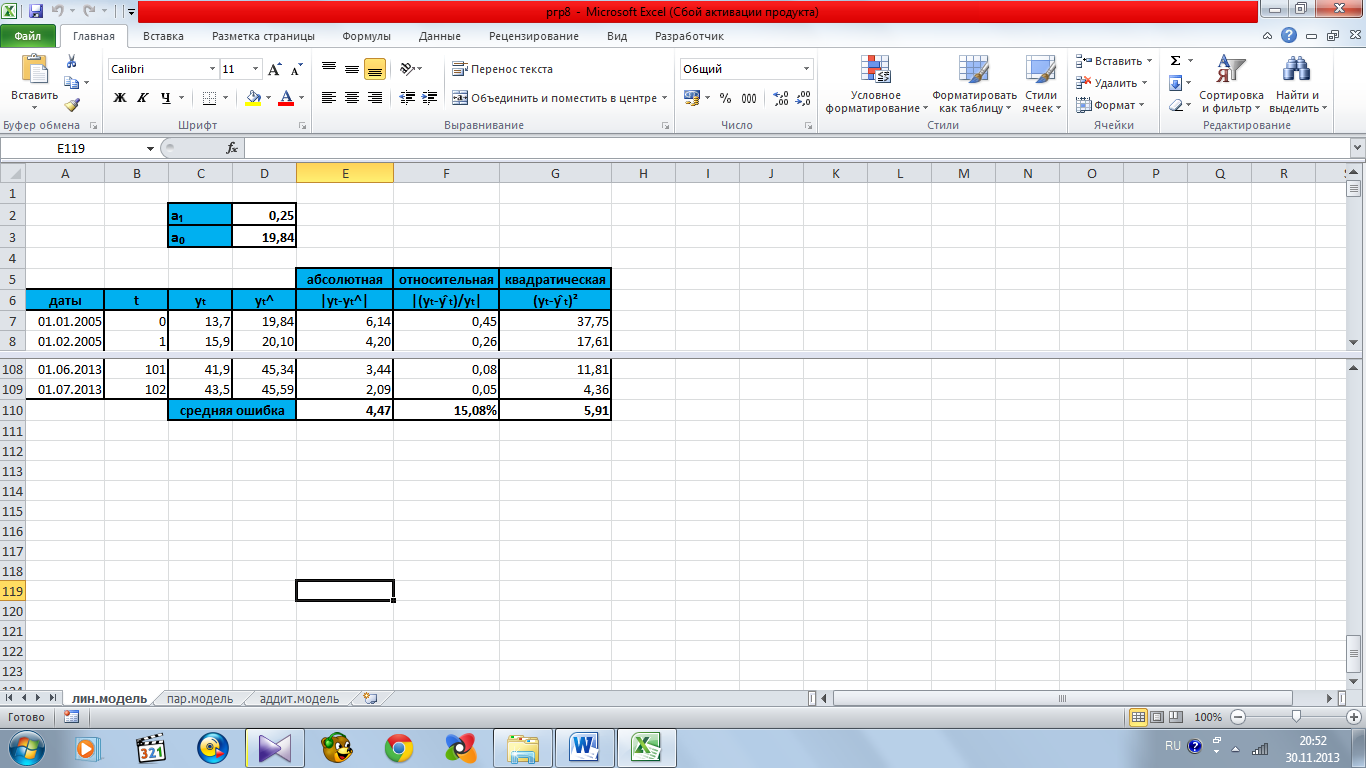
Рисунок 10.1 – расчет ошибок линейной модели по исходному временному ряду
Средняя
абсолютная ошибка составила
.
Средняя
относительная ошибка составила
.
Среднеквадратическая
ошибка составила
.
Определяются ошибки параболической модели по исходному временному ряду.
Была
построена параболическая модель по
уравнению
.
Далее рассчитаны ошибки. Результаты
показаны на рисунке 10.2.
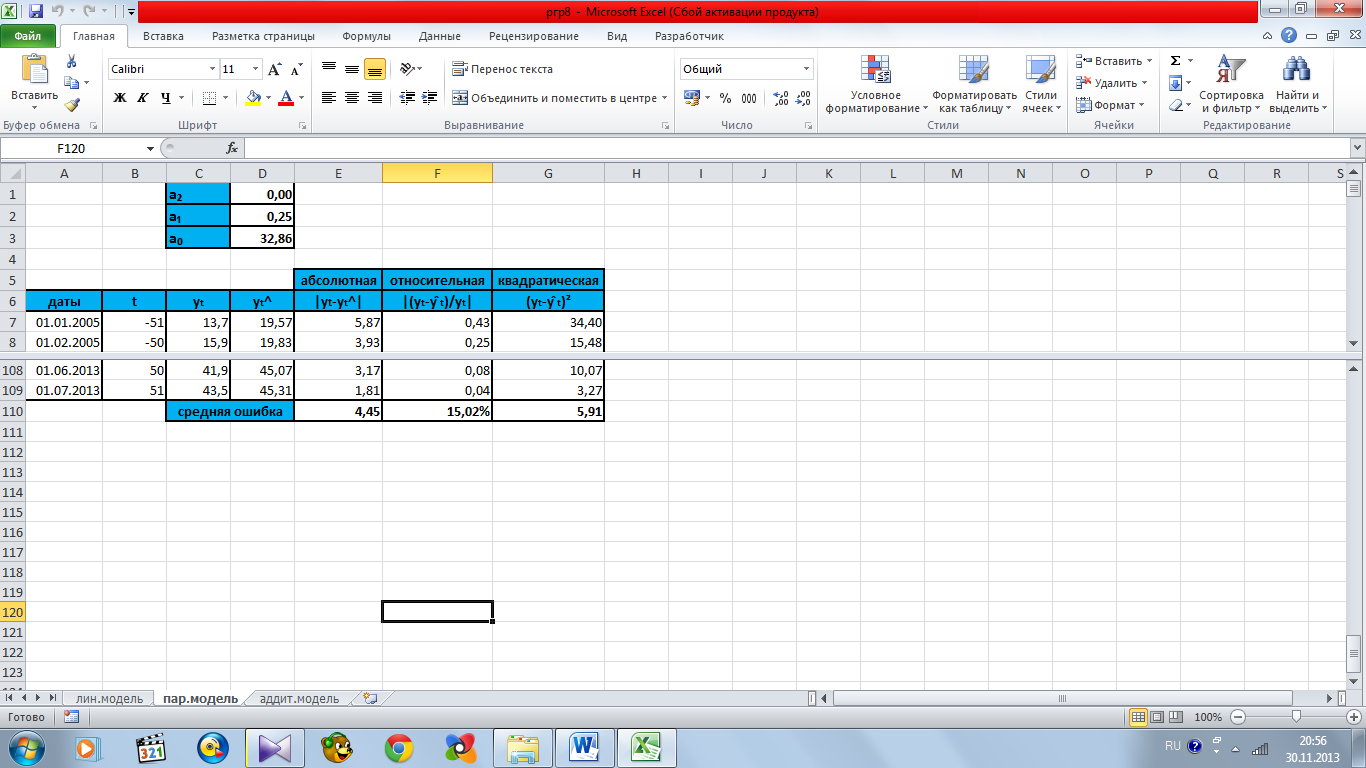
Рисунок 10.2 – расчет ошибок параболической модели по исходному временному ряду
Средняя
абсолютная ошибка составила
.
Средняя
относительная ошибка составила
.
Среднеквадратическая ошибка составила
Определяются
ошибки аддитивной модели по исходному
динамическому ряду. Была построена
модель по уравнению
.
Далее рассчитаны ошибки. Результаты
показаны на рисунке 10.3.
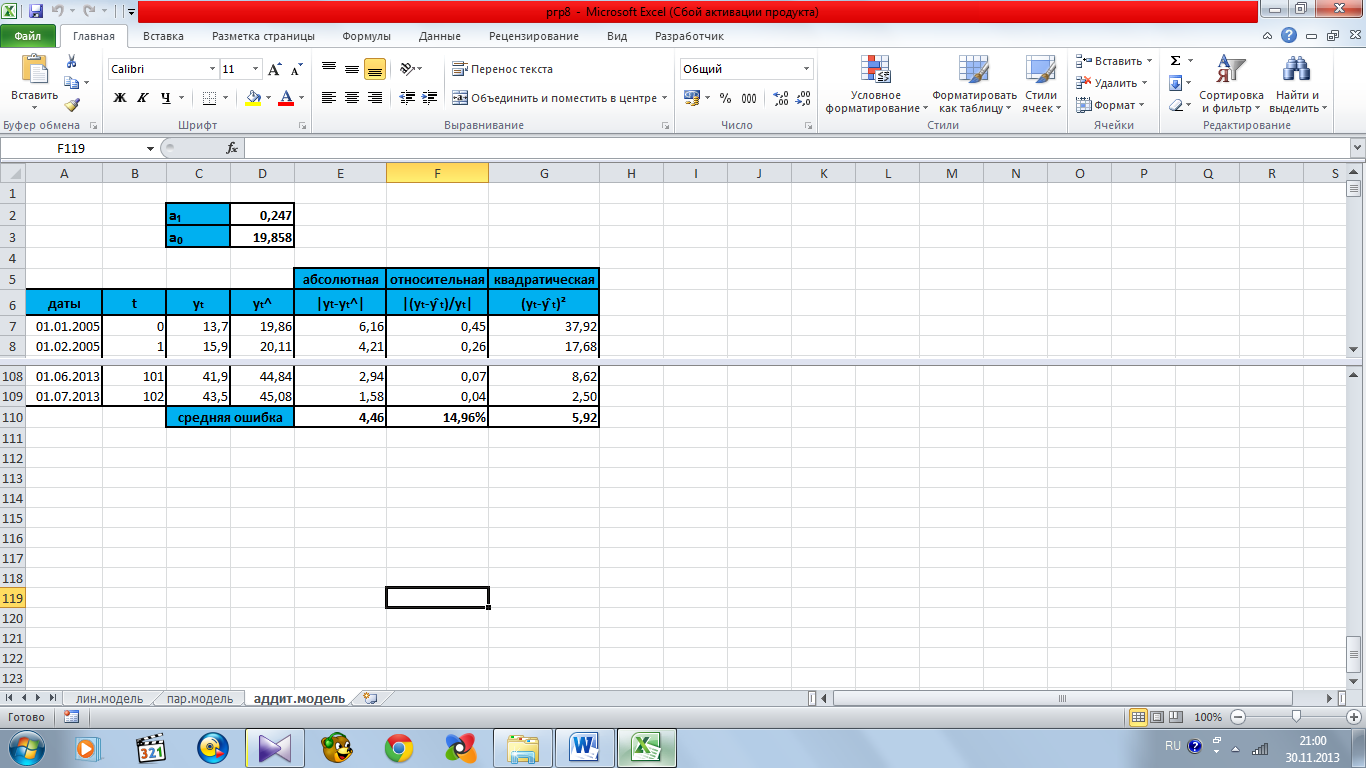
Рисунок 10.3 – расчет ошибок аддитивной модели по исходному временному ряду
Средняя
абсолютная ошибка составила
.
Средняя
относительная ошибка составила
.
Среднеквадратическая
ошибка составила
.
Сравнение ошибок моделей
Таблица 10.1- сравнение ошибок моделей
модель |
средняя абсолютная ошибка |
средняя относительная ошибка |
средняя квадратическая ошибка |
линейная |
|
|
|
параболическая |
|
|
|
аддитивная |
|
|
|
По выполненным расчетам можно сделать вывод о том, что оценки параметров более точны по исходному временному ряду у линейной модели и у аддитивной модели.
11. Экспоненциальное сглаживание в ms Excel
В предыдущих работах при анализе временных рядов использовался метод скользящей средней, в котором все данные, независимо от периода их возникновения, являются равноправными. Существует и другой способ, в котором данным приписываются веса, более поздним данным придается больший вес, чем более ранним.
Метод экспоненциального сглаживания в отличие от метода скользящих средних еще и может быть использован для краткосрочных прогнозов будущей тенденции на один период вперед и автоматически корректирует любой прогноз в свете различий между фактическим и спрогнозированным результатом. Именно поэтому метод обладает явным преимуществом над ранее рассмотренным методом.
Название метода происходит из того факта, что при его применении получаются экспоненциально взвешенные скользящие средние по всему временному ряду. При экспоненциальном сглаживании учитываются все предшествующие наблюдения – предыдущее учитывается с максимальным весом, предшествующее ему – с несколько меньшим, самое ранее наблюдение влияет на результат с минимальным статистическим весом.
Алгоритм расчета экспоненциально сглаженных значений в любой точке ряда i основан на трех величинах:
фактическое значение
в данной точке ряда
;прогноз в точке ряда
;некоторый заранее заданный коэффициент сглаживания α, постоянный по всему ряду.
Новый
прогноз можно записать формулой
.
В MS Excel для построения экспоненциальных сглаженных рядов используется пакет анализа данных.
Сравнивая график фактических данных с графиком прогноза, можно сделать вывод о том, что прогноз, полученный сглаживанием, реагирует на скачок фактической функции, но медленнее, чем хотелось бы. Реакция будет возможно более быстрой, если уменьшить значение фактора затухания.
В работе был сделан прогноз при факторах затухания, равном 0,8; 0,7; 0,9. Выбор параметров представлен соответственно на рисунке 11.1.
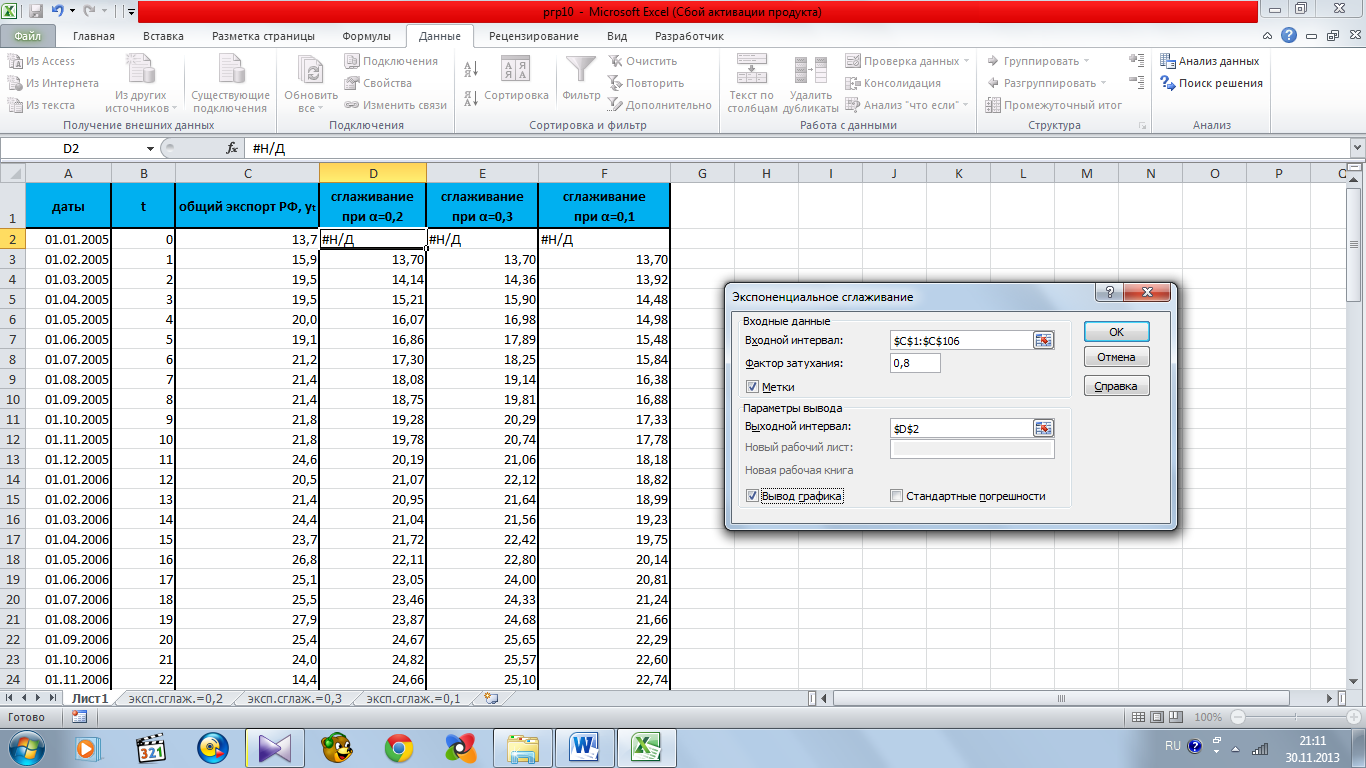
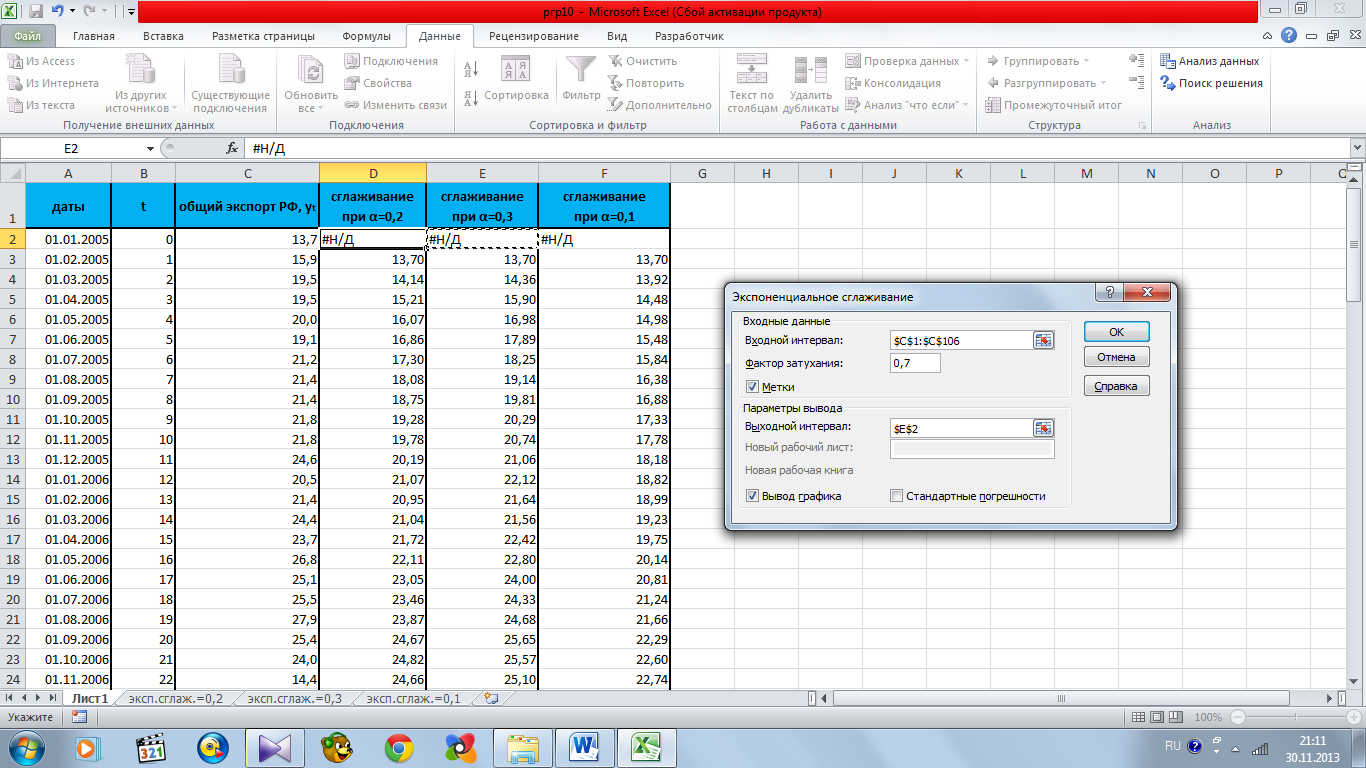
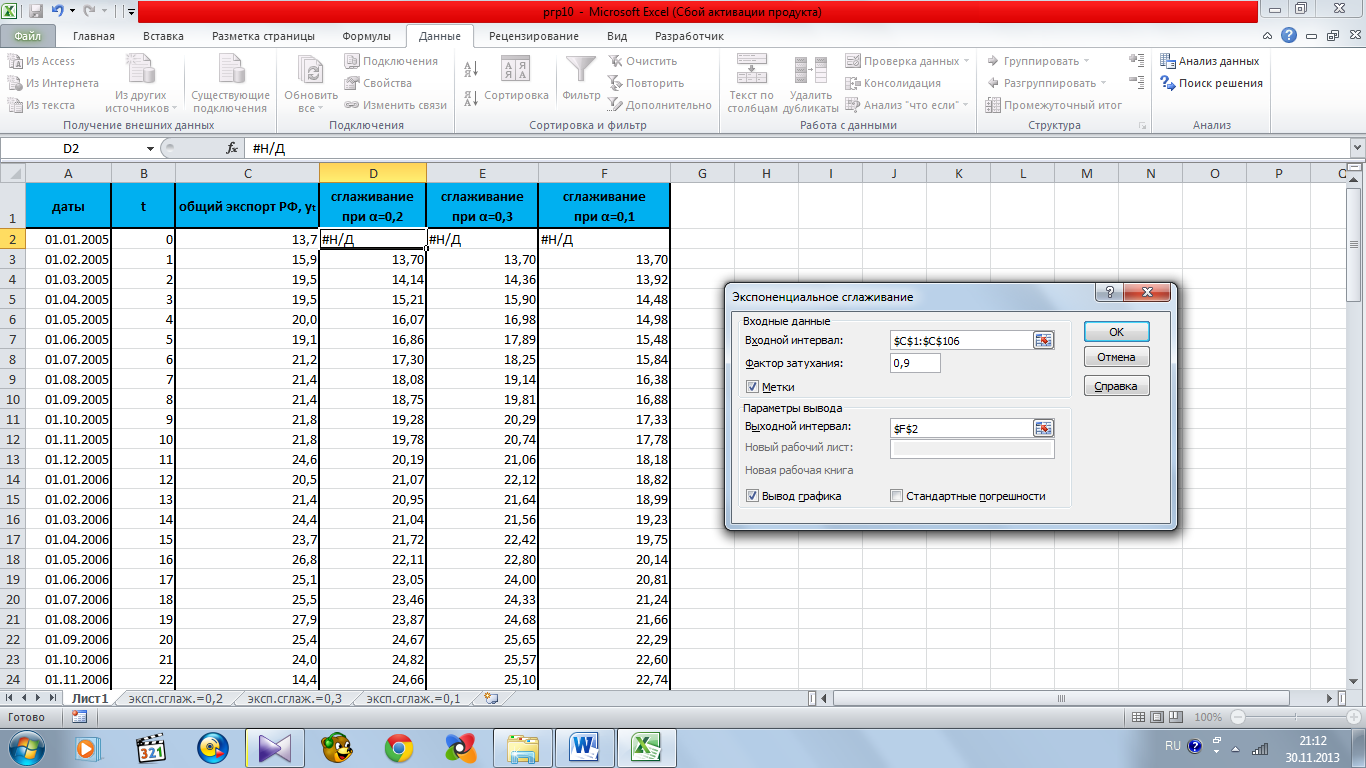
Рисунок 11.1 – выбор параметров при сглаживающем коэффициенте α=0,2; α=0,3; α=0,1
Результаты прогноза показаны на рисунке 11.2.
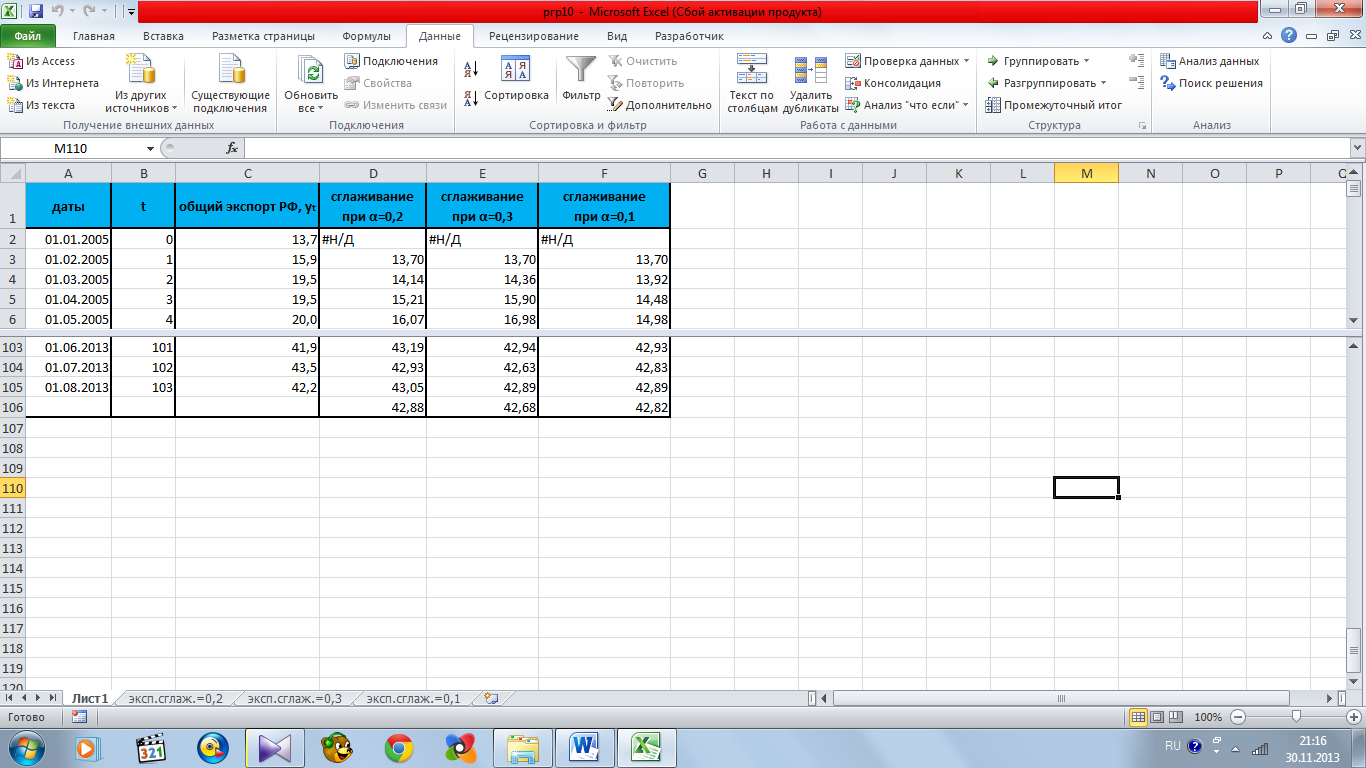
Рисунок 11.2 – прогноз
На рисунках 11.3, 11.4, 11.5 показан график при экспоненциальном сглаживании при разных параметрах.
Из графиков видно, что значения прогноза получаются наиболее близкими к реальным исходным данным при факторе затухания, равном 0,7. Поэтому лучше использовать модель при затухающем коэффициенте, равном α=0,3.
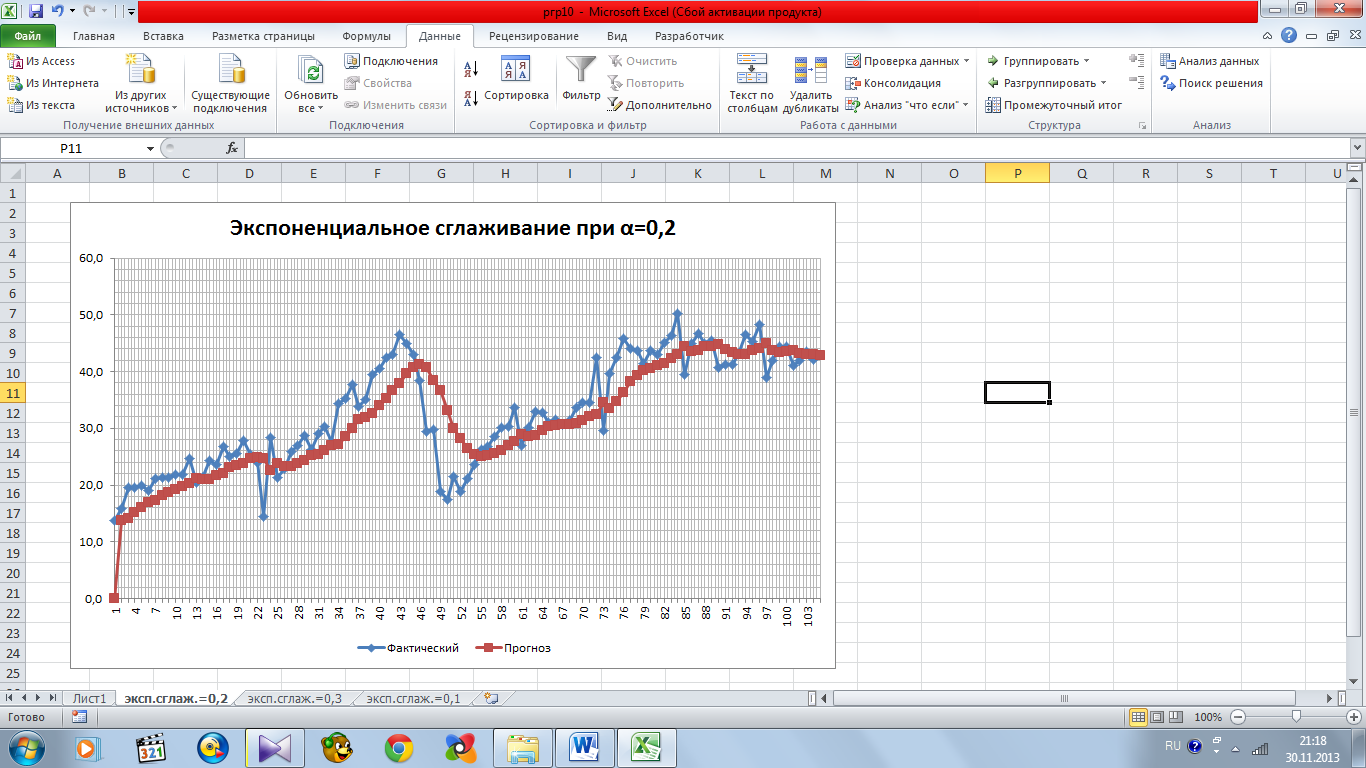
Рисунок 11.3 – экспоненциальное сглаживание при α=0,2
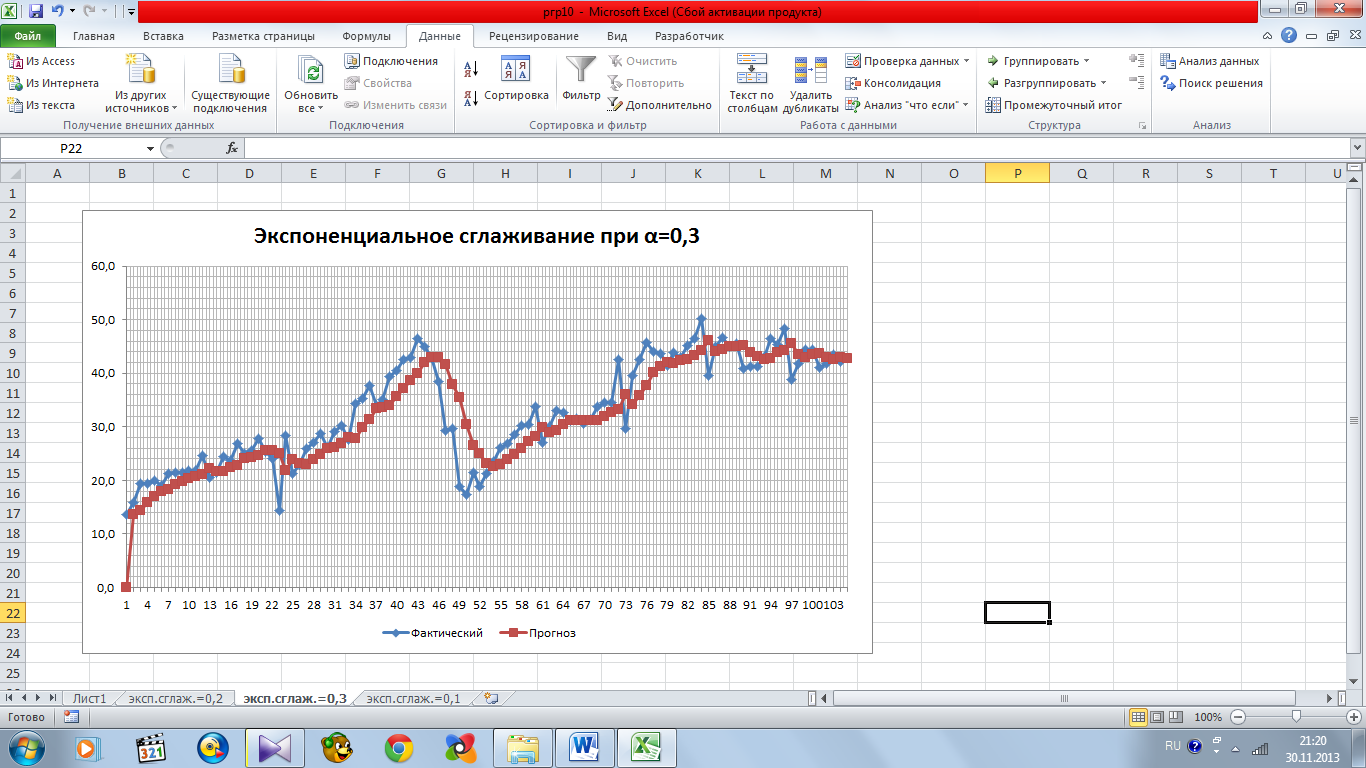
Рисунок 11.4 – экспоненциальное сглаживание при α=0,3
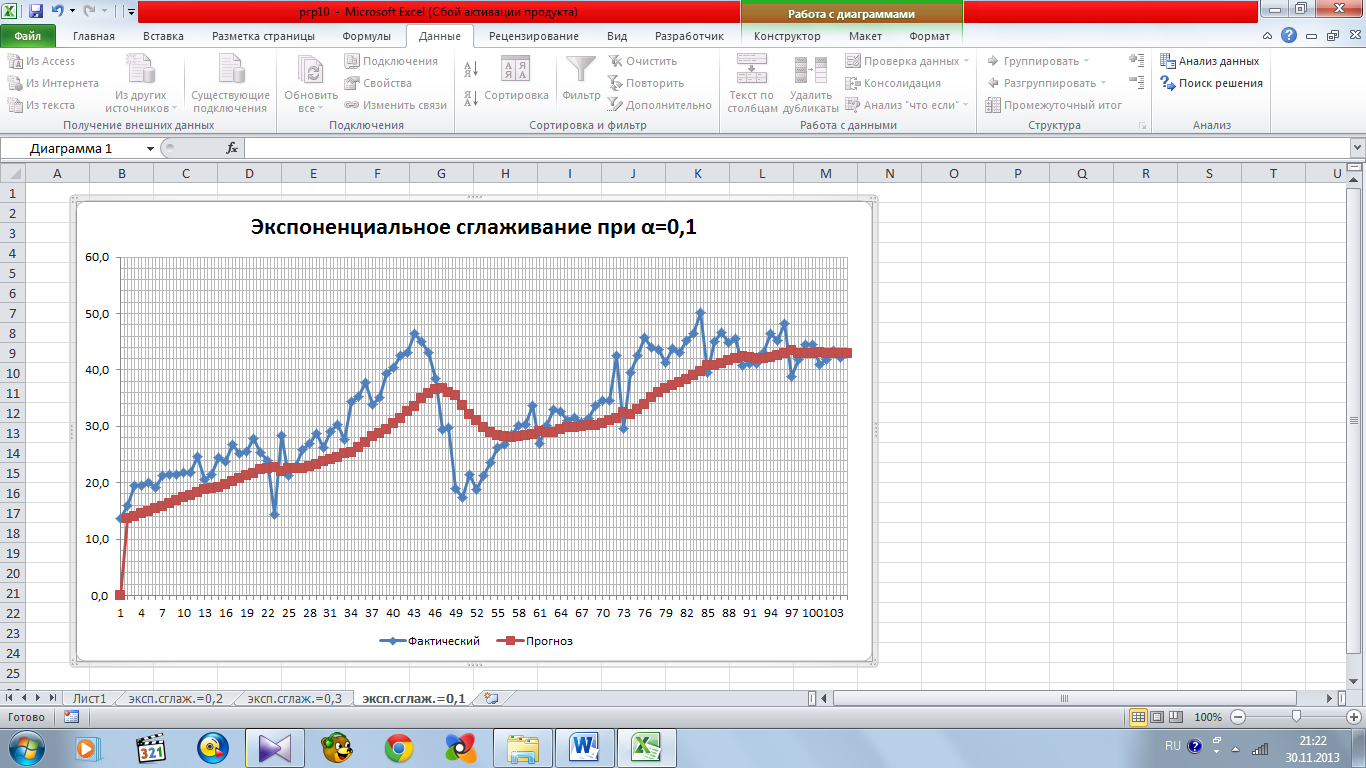
Рисунок 11.5 – экспоненциальное сглаживание при α=0,1