7. Оценка качества моделей (для кривых роста)

Данный анализ выполняется на примере ранее полученных результатов. В ней были определены гипотезы о независимости остатков при помощи нахождения наблюдаемого значения Дабрина-Уотсона и нормальности остатков с вычислением коэффициентов асимметрии и эксцесса.

На этом шаге предстоит проверить случайность остатков, рассчитывая количество поворотных точек, центрированность остатков с помощью критерия Стьюдента, а также охарактеризовать точность модели.

Проверяется ряд на случайность остатков.

Если остаток модели при сравнении с двумя соседними точками ряда остатков и окажется меньше или больше их, то данная точка является поворотной.

Было определено количество поворотных точек в ряду. Например, для первого уровня расчет показан на рисунке 7.1.

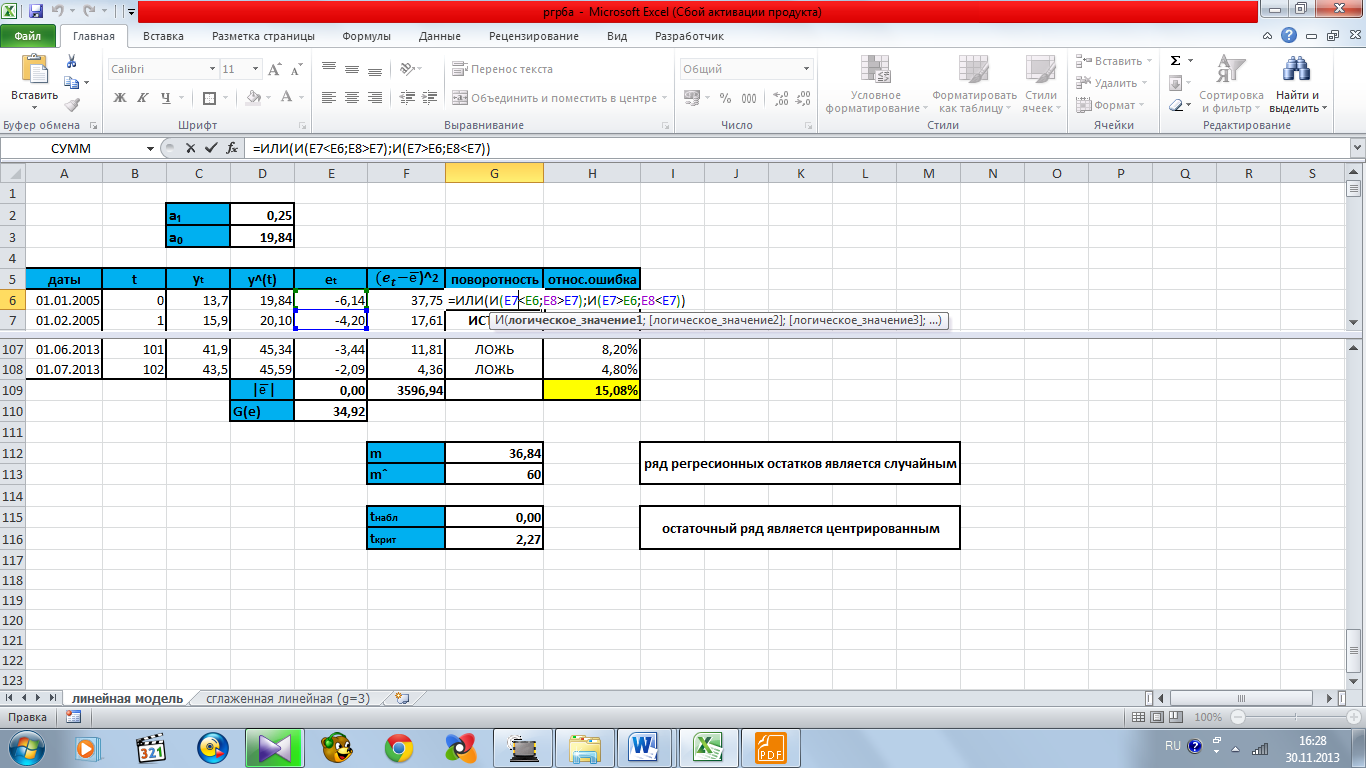
Рисунок 7.1 – определение поворотности точки для первого уровня

Значение «ЛОЖЬ» означает, что тока не является поворотной.

Значение «ИСТИНА» означает, что точка является поворотной.

Ряд остатков модели считается случайным, если выполняется условие: > = =36,84

Количество поворотных точек равно при исходных данных – 60, то есть . Количество поворотных точек равно при сглаженных данных – 36, то есть .

В первом случае > говорит о том, что ряд регрессионных остатков является случайным. Во втором случае < говорит о том, что ряд регрессионных остатков не является случайным.

Далее идет проверка гипотезы центрированности остатков. Для этого нужно определить среднее арифметическое значение остаточного члена и среднеквадратическое отклонение остаточного ряда , где в обоих случаях и (при исходных данных) и (при сглаженных данных); и рассчитываются соответственно по следующим формулам:

и , где N=103 и α=0,05.

В результате расчетов получили в обеих моделях и (функция СТЬЮДРАСПОБР). < 2,27, что говорит о том, что остаточный ряд в обеих моделях (и при исходных, и при сглаженных данных) является центрированным.

Далее дается характеристика точности модели.

Критерием точности модели является относительная ошибка, рассчитываемая по формуле δ(t)= |·100%≤13%. Если относительная ошибка не превышает 13%, то точность модели признается удовлетворительной.

Δ(t)= |·100%=15,076% - при исходных данных – точность модели неудовлетворительная;

δ(t)= |·100%=13,547% - при сглаженных данных – точность модели неудовлетворительная.

Поэтому, исходя из вычислений, можно сделать вывод о том, что использование обеих моделей неэффективно, поэтому стоит применить другой метод прогнозирования.

8. Статистический анализ и прогнозирование сезонных колебаний

Процедуры расчета сезонной составляющей зависят от принятой модели временного ряда, содержащей сезонность в аддитивной и мультипликативной форме. При этом для аддитивной модели характеристики сезонности будут измеряться в абсолютных величинах, для мультипликативных – в относительных.

Мультипликативная модель

Сезонные колебания проявляются каждые 12 месяцев, поэтому для вычисления значений скользящей средней используют формулу:

Расчет значения для I уровня ряда производится следующим образом:

Аналогичным образом рассчитываются значения до последнего уровня при n=104.

Следующим шагом является определений уровней , которые отражают влияние случайных факторов к сезонности. Для этого используют формулу: .

Результаты вычислений показаны на рисунке 8.1.

На следующем шаге определяются значения десезонализированного ряда y_t¹. Предварительную оценку сезонности получают усреднением уровней временного ряда для одноименных месяцев. На примере показана оценка сезонности для января:

Рисунок 8.1 – расчет и

Аналогичным образом рассчитываются для всех месяцев. Далее рассчитывается сумма по ряду , которая равняется 11,984. Данная сумма должна равняться 12. Так как примерно равна 12, то найденные ошибки сезонности можно бы оставить в неизменном виде, так как процедура корректировки приведет к незначительному изменению. Однако корректировку данных оценок сезонности следует провести. Для этого определяем поправочный коэффициент, рассчитываемый как:

.

Тогда с учетом этого получаем окончательные оценки сезонности, в примере приведен расчет оценки для января.

.

Аналогичным образом вычисляем все значения . . 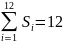Результаты вычислений показаны на таблице 8.1.

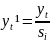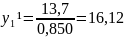Чтобы найти значения десезонализированного ряда, используют следующую формулу: . Расчет значения . Аналогичным образом считают для всех остальных 103 наблюдений.

Таблица 8.1 – оценка сезонности для мультипликативной модели

	x̄			Si
x1	0,849		S1	0,850
x2	0,921		S2	0,922
x3	1,010		S3	1,011
x4	0,996		S4	0,998
x5	1,024		S5	1,026
x6	0,994		S6	0,995
x7	1,035		S7	1,037
x8	1,053		S8	1,054
x9	1,024		S9	1,025
x10	1,038		S10	1,039
x11	0,940		S11	0,941
x12	1,100		S12	1,101
сумма	11,984		сумма	12,000
k	1,001

Следующим шагом является определение расчетных уровней объема общего экспорта . Для описания тенденции воспользуемся моделью линейного тренда, так как это согласуется с результатами графического анализа динамики показателей (рисунок 8.2), в ходе которого получено уравнение и . Используется формула: .

Далее рассчитываем относительную ошибку прогноза по формуле и среднюю относительную ошибку для всего временного ряда, используя формулу δ(t)= |·100%≤13%.

Все расчеты показаны на рисунке 8.3.

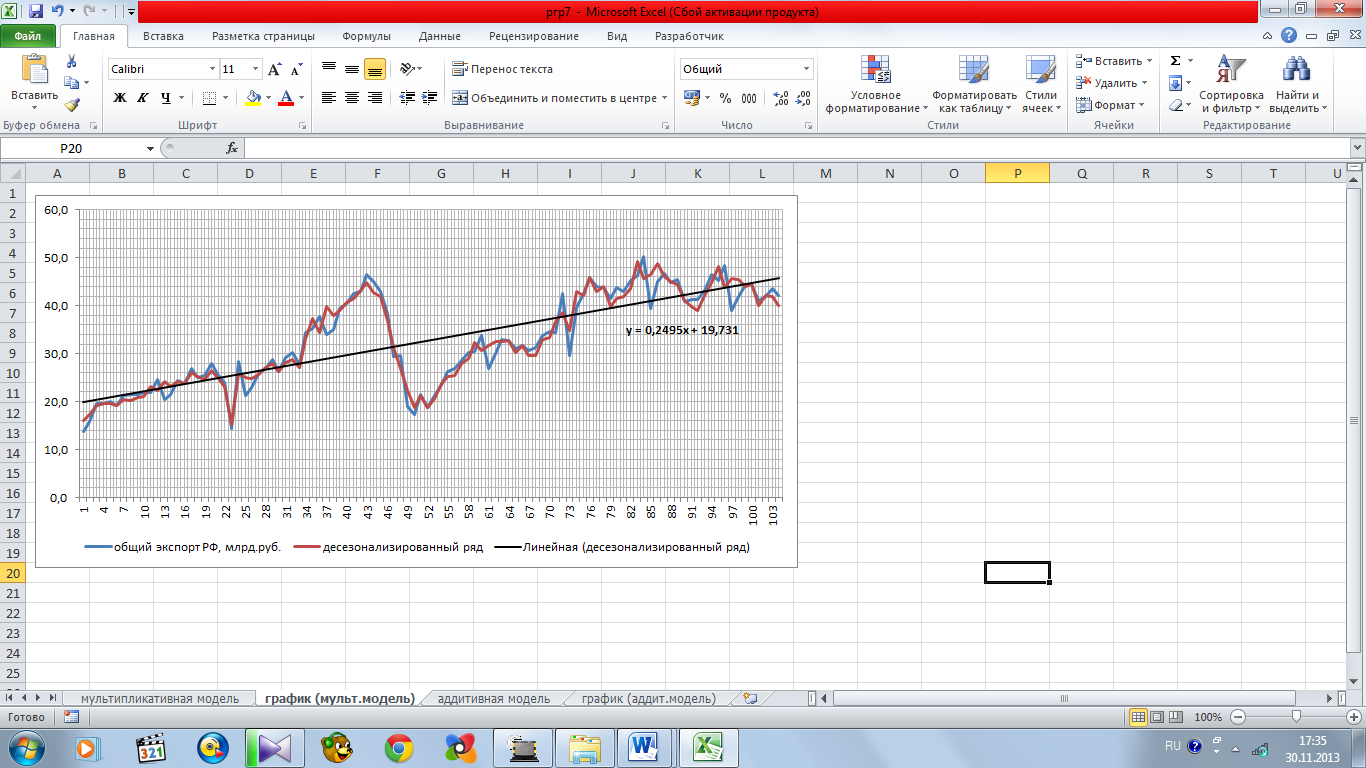
Рисунок 8.2 – построение линейного тренда

Рисунок 8.3 – расчет показателей по мультипликативной модели

δ(t)= 13,677% характеризует точность модели, средняя относительная ошибка превышает нормируемое значение, поэтому ее не рекомендуется применить при прогнозировании. В ходе расчетов был сделан прогноз конец 2013г., то есть на 4 месяца (с сентября по декабрь), полученная с помощью формулы. Данные приведены в таблице 8.2.

Таблица 8.2 – данные прогнозов

прогноз
дата	t
01.09.2013	105	39,04
01.10.2013	106	42,59
01.11.2013	107	46,95
01.12.2013	108	46,58

Аддитивная модель

Сезонные колебания проявляются каждые 12 месяцев, поэтому для вычисления значений скользящей средней используют формулу:

Расчет значения для I уровня ряда производится следующим образом:

Аналогичным образом рассчитываются значения до последнего уровня при n=104.

Следующим шагом является определений уровней , которые отражают влияние случайных факторов к сезонности. Для этого используют формулу:

.

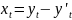Результаты вычислений показаны на рисунке 8.4.

Рисунок 8.4 – расчет и

На следующем шаге определяются значения десезонализированного ряда y_t¹. Предварительную оценку сезонности получают усреднением уровней временного ряда для одноименных месяцев. На примере показана оценка сезонности для января:

Аналогичным образом рассчитываются для всех месяцев. Далее рассчитывается сумма по ряду , которая равняется 0,933. Данная сумма должна примерно равняться 0. Проведем корректировку значений сезонной составляющей. Определяем поправочный коэффициент, рассчитываемый как:

.

Тогда с учетом этого получаем окончательные оценки сезонности, в примере приведен расчет оценки для января.

.

Аналогичным образом вычисляем все значения . . Результаты вычислений показаны на таблице 8.3.

Таблица 8.3 – оценка сезонности для аддитивной модели

	x̄			Si
x1	-4,943		S1	-5,021
x2	-2,193		S2	-2,270
x3	0,593		S3	0,516
x4	0,317		S4	0,240
x5	0,945		S5	0,867
x6	-0,165		S6	-0,243
x7	1,056		S7	0,978
x8	1,572		S8	1,494
x9	0,708		S9	0,631
x10	1,224		S10	1,146
x11	-1,436		S11	-1,514
x12	3,254		S12	3,176
сумма	0,933		сумма	0,000
k	0,078

Чтобы найти значения десезонализированного ряда, используют следующую формулу: . Расчет значения . Аналогичным образом считают для всех остальных 103 наблюдений.

Следующим шагом является определение расчетных уровней численности безработных . Для описания тенденции воспользуемся моделью линейного тренда, так как это согласуется с результатами графического анализа динамики показателей (рисунок 8.5), в ходе которого получено уравнение 0,2473 + 19,858 где =19,858 и = 0,2473. Используется формула: .

Далее рассчитываем относительную ошибку прогноза по формуле и среднюю относительную ошибку для всего временного ряда, используя формулу δ(t)= |·100%≤13%.

Все расчеты показаны на рисунке 8.6.

Рисунок 8.5 – построение линейного тренда по аддитивной модели

Рисунок 8.6 – расчет показателей по аддитивной модели

δ(t)= 13,606% характеризует точность модели, средняя относительная ошибка превышает норму. В ходе расчетов были сделаны прогнозы на конец 2013г. при помощи формулы . Данные приведены в таблице 8.4.

Рассматривая исходный динамический ряд, была видна небольшая сезонность.

Таблица 8.4 – данные прогнозов

прогноз
дата	t
01.09.2013	105	40,80
01.10.2013	106	43,80
01.11.2013	107	46,83
01.12.2013	108	46,81

Сравнивая мультипликативные и аддитивные модели, был сделан вывод о том, что последняя более походит для описания данного временного ряда, точность аддитивной более высока, чем у мультипликативной.