5. Построение кривых роста (функций времени)

Для отображения основной тенденции развития явления во времени или модели этого процесса применяются различные уравнения: полиномы разной степени, экспоненты, логистические кривые и другие функции времени или кривые роста.

Определим линейный тренд для исходного динамического ряда, отображающего денежные доходы в среднем на душу населения в месяц. После всех произведенных преобразований точечная диаграмма имеет следующий вид представленный на рисунке 5.1.

Рисунок 5.1 – диаграмма динамики общего экспорта РФ

Добавим линию тренда для исследуемого динамического ряда, определим функцию аппроксимации – линейная. Получим диаграмму представленную на рисунке 5.2.

Рисунок 5.2 – линейная модель тренда

Подбор выравнивающей кривой с использованием линейной аппроксимирующей функции позволил определить уравнение линейного тренда для исходного динамического ряда:

при

Определим уравнение тренда на основании экспоненциального выравнивания (рисунок 5.3).

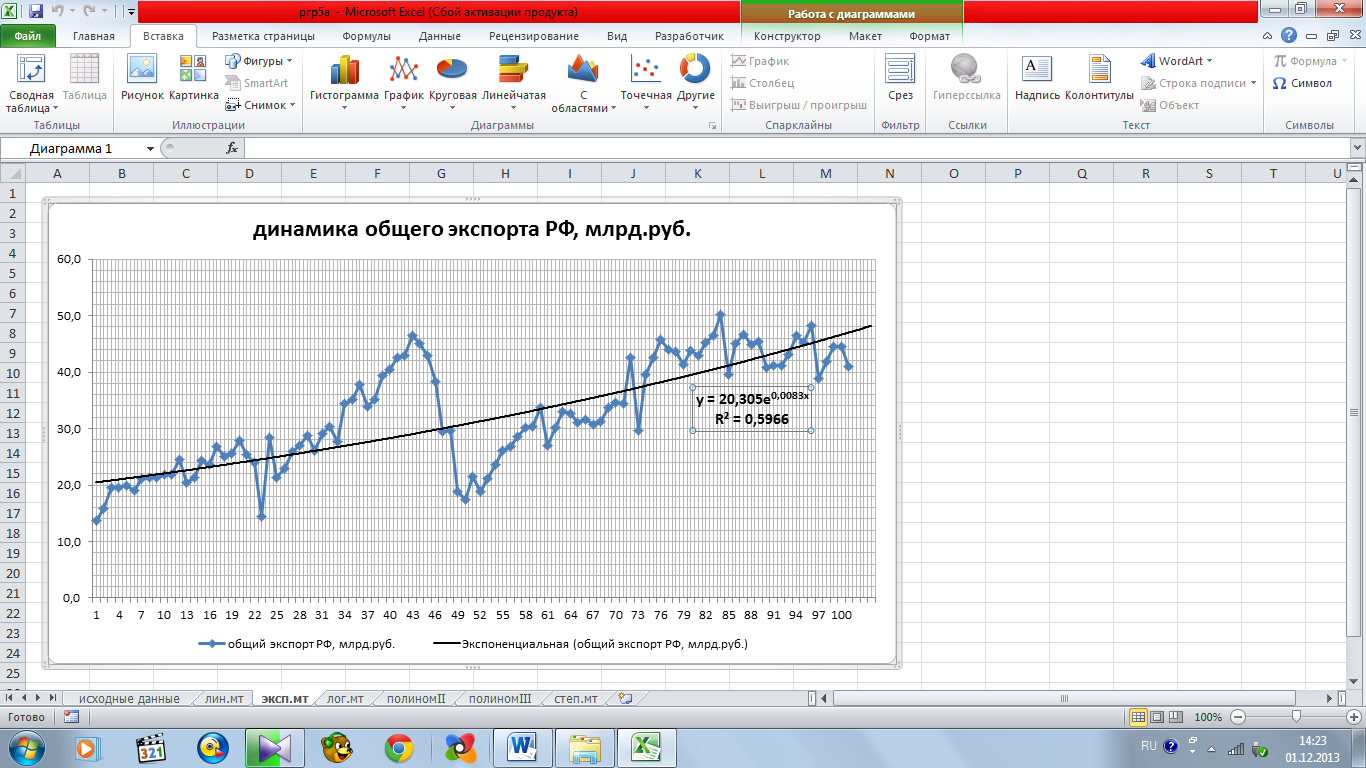
Рисунок 5.3 – экспоненциальная модель тренда

Подбор выравнивающей кривой с использованием экспоненциальной аппроксимирующей функции позволил определить уравнение тренда для исходного динамического ряда:

при

Определим уравнение тренда на основании логарифмического выравнивания (рисунок 5.4).

Подбор выравнивающей кривой с использованием логарифмической аппроксимирующей функции позволил определить уравнение тренда для исходного динамического ряда:

при

Рисунок 5.4 – логарифмическая модель тренда

Определим уравнение тренда на основании выравнивания с использованием полинома второго порядка (рисунок 5.5).

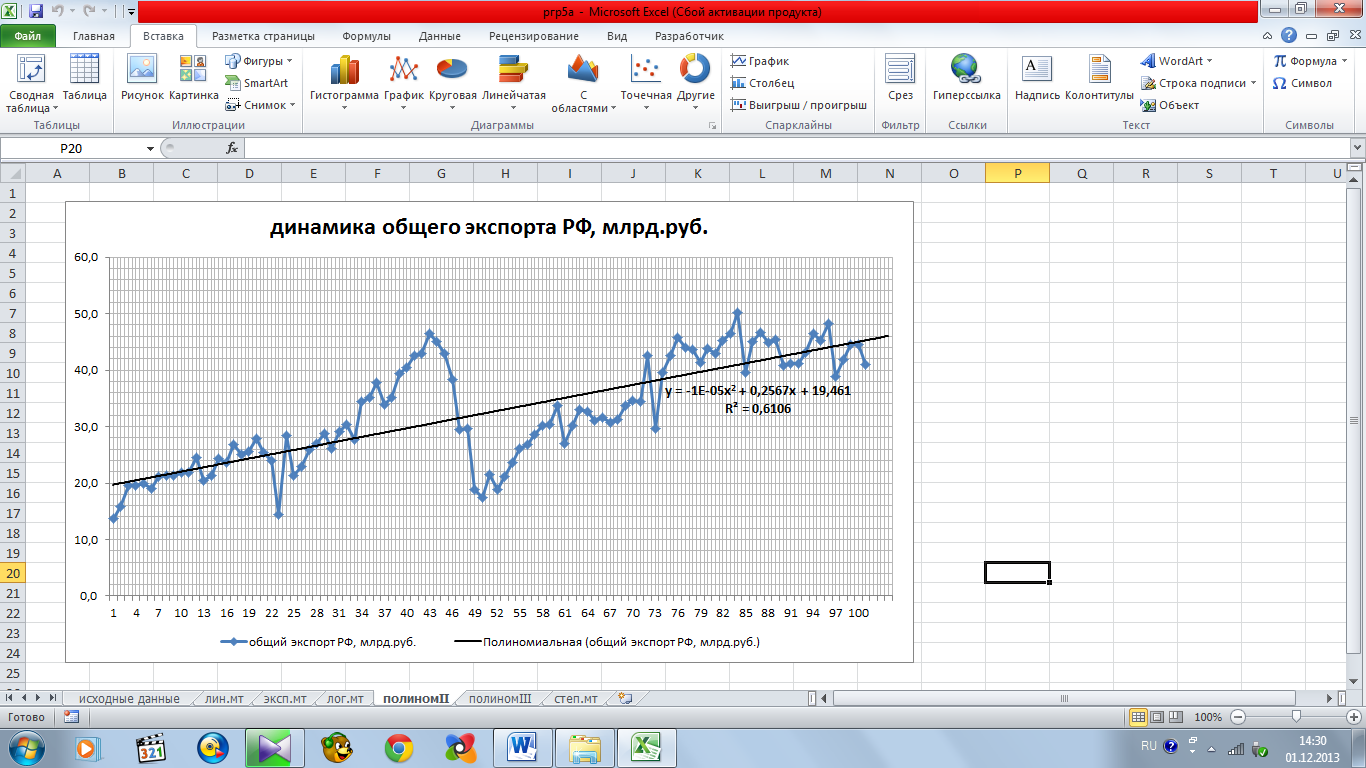
Рисунок 5.5 – полиномиальная модель тренда II порядка

Подбор выравнивающей кривой с использованием аппроксимирующего полинома второго порядка позволил определить уравнение тренда для исходного динамического ряда:

при

Определим уравнение тренда на основании выравнивания с использованием полинома третьего порядка (рисунок 5.6).

Рисунок 5.6 – полиномиальная модель тренда III порядка

Подбор выравнивающей кривой с использованием аппроксимирующего полинома третьего порядка позволил определить уравнение тренда для исходного динамического ряда:

при

Определим уравнение тренда на основании степенного выравнивания (рисунок 5.7).

Рисунок 5.7 – степенная модель тренда

Подбор выравнивающей кривой с использованием степенного тренда позволил определить уравнение тренда для исходного динамического ряда:

при

1. Оценка качества подобранных моделей.

Одним из способов сравнения качества подобранных моделей является метод сравнения коэффициентов детерминации. Чем выше коэффициент детерминации, тем точнее построена модель и точнее прогнозы на следующие периоды. Данные полученные при расчете представлены в таблице 5.1. Из них видно, что наибольший коэффициент детерминации имеет полиномиальная модель тренда III порядка, он равен 0,6245. Второй ранг имеет полиномиальная модель II степени и линейная модель тренда, их коэффициент равен 0,6106.

Реальные данные на 01.06.2013, 01.07.2013, 01.08.2013 составляют 41,9, 43,5, 42,2 млрд.рублей.

Таблица 5.1 – коэффициенты детерминации и прогнозы

вид модели	уравнение	R²	ранг	прогноз
линейная			II	45,56
				45,82
				46,02
экспоненциальная			IV	47,35
				47,74
				48,14
логарифмическая			VI	39,91
				39,98
				40,06
полином II степени			II	45,54
				45,80
				46,05
полином III степени			I	-129939,12
				-129929,32
				-129919,52
степенная			V	40,00
				40,10
				40,21

В данной работе было построено 6 наиболее популярных моделей тренда, а именно линейную, экспоненциальную, логарифмическую, полиномиальную второй и третьей степени и степенную модель тренда. Также найдены уравнения тренда и коэффициенты R², все они представлены в таблице 5.1. На основании полученных данных можно сделать вывод о том, что для данной модели не подходит ни одна из представленных моделей тренда, так как они имеют слишком низкую величину достоверности и аппроксимации. Однако, если судить по полученным прогнозам, то лучше для применять для прогнозирования полиномиальную модель тренда II порядка, учитывая возможный дальнейший рост объема экспорта РФ.