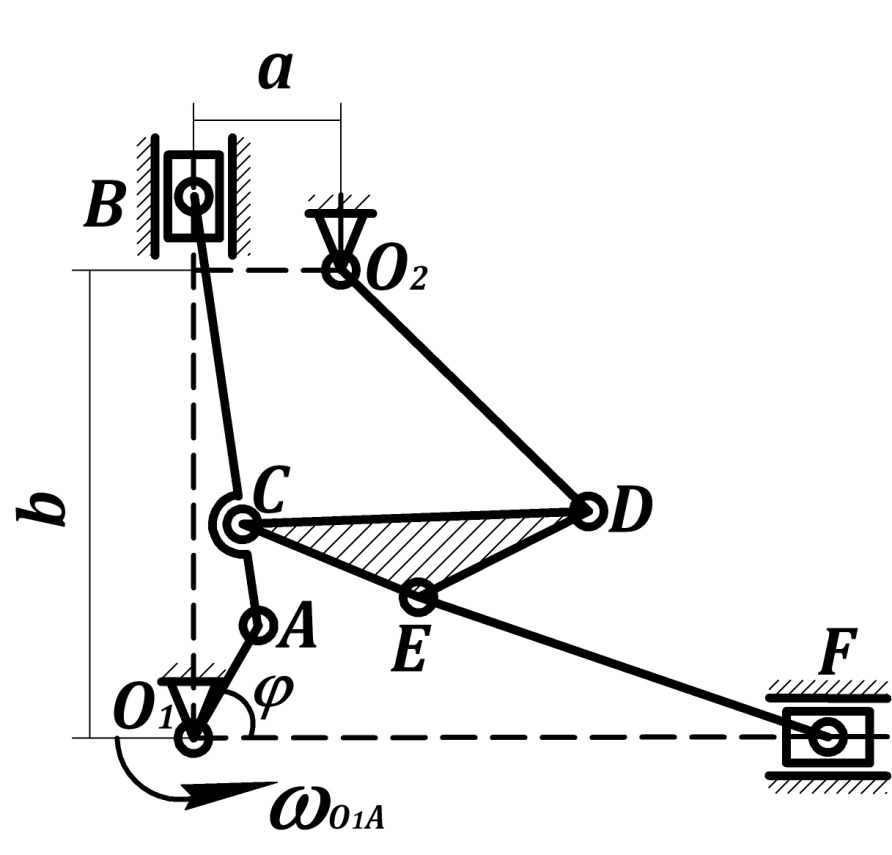
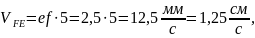- •Порядок построения схемы механизма:
- •Определение линейных скоростей точек a, b, c, d, e, f механизма и угловых скоростей его звеньев ab, cde, o2d, ef при помощи плана скоростей
- •Определение скоростей точек a, b, c, d, e, f механизма и угловых скоростей его звеньев ab, cde, o2d, ef при помощи мгновенных центров скоростей
- •Определение линейных ускорений точек a, b, c механизма и углового ускорения звена ab
- •Определение положения мгновенного центра ускорений звена ав механизма.
- •Приложения
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КОВРОВСКАЯ ГОСУДАРСТВЕННАЯ ТЕХНОЛОГИЧЕСКАЯ АКАДЕМИЯ
ИМ. В. А. ДЕГТЯРЁВА»
ДОМАШНЕЕ ЗАДАНИЕ
ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
«КИНЕМАТИКА ПЛОСКОГО МЕХАНИЗМА»
СХЕМА (по № в списке группы), ВАРИАНТ ______
Руководитель: к. т. н., доц. Наумов Е. В.
Исполнитель: студент гр. ________ _______________
Ковров 2013
ИСХОДНЫЕ ДАННЫЕ
РАСЧЁТНАЯ СХЕМА
Схема 13
|
ТАБЛИЦА 1
№ вар. |
φ град. |
Расстояния (см) |
Длины звеньев (см) |
|||||||||
a |
b |
O1A |
O2D |
AB |
BC |
CD |
CE |
DE |
EF |
|||
1 |
60 |
17 |
54 |
15 |
40 |
50 |
35 |
40 |
22 |
22 |
50 |
|
Порядок построения схемы механизма:
М: 1 : 10 (1 см схемы = 10 см механизма или 1 мм схемы = 1 см механизма).
О1А = 15 мм под углом φ = 60о.
Радиусом АВ = 50 мм засечка точки В на вертикали О1В.
b = О1О2 = 54 мм.
a = 17 мм от вертикали О1В по горизонтали до точки О2.
Отложение ВС = 35 мм.
Радиусами CD = 40 мм и О2D = 40 мм определение точки D.
Радиусами CЕ = 22 мм и DЕ = 22 мм определение точки Е.
Радиусом EF = 50 мм определение точки F на горизонтали от точки О1.
Определение линейных скоростей точек a, b, c, d, e, f механизма и угловых скоростей его звеньев ab, cde, o2d, ef при помощи плана скоростей
Графическое
отображение представлено в приложении
I.
На схеме механизма точно по направлению
отображены векторы
 перпендикулярно
О1А,
перпендикулярно
О1А,
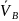 по линии О1В,
по линии О1В,
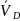 перпендикулярно O2D,
перпендикулярно O2D,
 по линии O1F.
Направления векторов
по линии O1F.
Направления векторов
 и
и
 отображены на схеме после построения
плана скоростей. Длины всех векторов
на схеме произвольны.
отображены на схеме после построения
плана скоростей. Длины всех векторов
на схеме произвольны.
Кривошип О1А:

Звено АВ:
Принимаем, что точка А – полюс, тогда:

Из произвольной точки О (в приложении I снизу механизма) проводим луч Оа, изображающий в выбранном масштабе М 1 : 5 скорость точки А:

Из
точки О
проводим прямую в направлении скорости
.
Из точки а
проводим прямую, перпендикулярную АВ
(образ
 ).
На пересечении этих прямых получаем
точку b.
Отрезок Оb
в масштабе определяет
).
На пересечении этих прямых получаем
точку b.
Отрезок Оb
в масштабе определяет
 :
:

Скорость равна:

Для
определения
 находим отрезок
находим отрезок
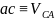 на отрезке аb.
Из выражения
на отрезке аb.
Из выражения
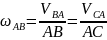
получаем пропорцию:

С плана скоростей:
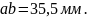
Из исходных данных:

Тогда:
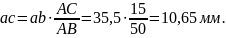
Отрезок Oс в масштабе определяет :

Угловая скорость звена АВ определяется по вращательной скорости точки В вокруг точки А (полюса):
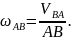
На
плане скоростей скорости
 соответствует отрезок аb,
тогда в масштабе получаем:
соответствует отрезок аb,
тогда в масштабе получаем:


Звенья CDE и O2 D:
Принимаем, что точка С – полюс, тогда:

Скорость
перпендикулярна звену O2D,
поэтому на плане скоростей из точки О
проводим луч перпендикулярно O2D
в направлении
.
Скорость
 перпендикулярна стороне DС
звена CDE,
поэтому из точки С
(из конца вектора
на плане скоростей) проводим луч
перпендикулярно DС.
На пересечении лучей из точек О
и С
получаем точку d.
Отрезок Od
в масштабе определяет
перпендикулярна стороне DС
звена CDE,
поэтому из точки С
(из конца вектора
на плане скоростей) проводим луч
перпендикулярно DС.
На пересечении лучей из точек О
и С
получаем точку d.
Отрезок Od
в масштабе определяет
 :
:

Угловая скорость звена O2D равна:

Относительно полюса С для скорости точки Е имеем векторное выражение:

Скорость
 перпендикулярна стороне ЕС
звена CDE,
поэтому на плане скоростей из точки С
проводим луч перпендикулярно ЕС
в направлении до пересечения с будущим
лучом Oe,
который определит скорость
.
Для звена CDE
угловая скорость будет:
перпендикулярна стороне ЕС
звена CDE,
поэтому на плане скоростей из точки С
проводим луч перпендикулярно ЕС
в направлении до пересечения с будущим
лучом Oe,
который определит скорость
.
Для звена CDE
угловая скорость будет:

Длина отрезка ce вычисляется из пропорции (напоминаем, что точка С – полюс):
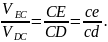
С плана скоростей: cd = 48.5 мм.
Из исходных данных: CE = 22 см, CD = 40 см.
Тогда:

С
плана скоростей отрезок Oe
в масштабе определяет
 :
:

Угловая скорость звена CDE определяется по вращательной скорости точки D вокруг полюса C:

С плана скоростей: cd = 48.5 мм.
В масштабе получаем:
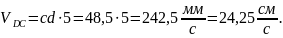
Из исходных данных: CD = 40 см.
Тогда:

Звено EF:
Принимаем, что точка E – полюс, тогда:

Скорость
направлена по горизонтальной прямой
O1F,
поэтому на плане скоростей из точки О
проводим луч в направлении
.
Скорость
 перпендикулярна звену EF,
поэтому из точки e
(из конца вектора
на плане скоростей) проводим луч
перпендикулярно EF.
На пересечении лучей из точек О
и e
получаем точку f.
Отрезок Of
в масштабе определяет
перпендикулярна звену EF,
поэтому из точки e
(из конца вектора
на плане скоростей) проводим луч
перпендикулярно EF.
На пересечении лучей из точек О
и e
получаем точку f.
Отрезок Of
в масштабе определяет
 :
:

Угловая скорость звена EF определяется по вращательной скорости точки F вокруг полюса E:

На плане скоростей скорости соответствует отрезок ef, перпендикулярный EF:

Тогда в масштабе получаем: