3.4. Распределение Пуассона

Вероятность того, что в течение времени t произойдет ровно m событий, определяется по формуле:

Распределение Пуассона показывает вероятность наступления определенного числа событий за данный промежуток времени. В логистике с помощью формулы Пуассона определяется вероятность поступления автомашин на базу, например, в течение одного часа. Из этого следует, что формула Пуассона моделирует случайный процесс поступления заявок на то или иное обслуживание, именно поэтому формула Пуассона является одной из основных в теории массового обслуживания.

5. Сравнение законов распределения вероятностей: критерии согласия

В теории вероятностей разработаны методы, позволяющие оценивать степень соответствия фактических распределения вероятностей их теоретическим значениям. С этой целью используется так называемые критерии согласия, наиболее известным из которых является критерий χ² («критерий хи-квадрат»). Указанный критерий позволяет сравнивать между собой эмпирические законы распределения, полученные по одним и тем же исходным фактическим данным.

Чем меньше значение χ ², тем лучше данный эмпирический закон согласуется с теоретическим. Для сравнения эмпирических законов распределения вероятностей вычисляются значения χ ² по следующей формуле:

где п_ф и п_т – соответственно фактические и теоретические значения частот исследуемых законов распределения.

Величина χ ² также является случайной, а поэтому подчиняется своему закону распределения. Методический подход к сравнению эмпирических законов распределения иллюстрируется примером.

Следует установить, какой закон распределения вероятностей – нормальный или экспоненциальный – лучше отражает распределение данной величины, т.е. осуществляется проверка гипотез. В качестве исследуемой величины прият объем реализации (продаж) определенного товара. Исходные данные о реализации товара представлены в табл. 3.2.

Таблица 3.2

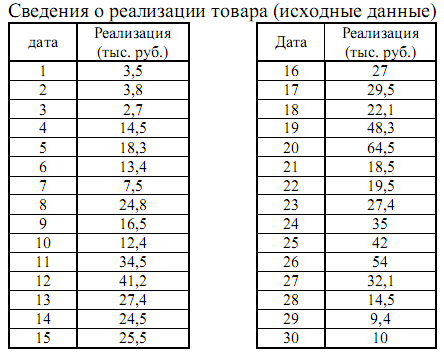
Задача формулируется следующим образом: построить распределение вероятностей величины спроса на данный товар, если в результате проведенного исследования получены результаты о реализации, в тыс. руб. в день.

Для построения нормального и экспоненциального законов распределения вероятностей вычисляются среднее значение реализации товара в день х , среднеквадратическое отклонение σ, а также параметр экспоненциального закона λ. Для расчета указанных величин ряд фактических данных упорядочивается от х_min до х_max. Необходимые вычисления представлены в табл. 3.3.

П о итогам табл. 3.3 получаем:

Далее следует установить интервалы значений и вычислить фактические частоты двумя способами:

а) через нормальное распределение (табл. 3.4, рис. 3.4)

Таблица 3.4

Рис. 3.4. Нормальный закон распределения вероятностей

б) через экспоненциальное распределение (табл. 3.5, рис. 3.5)

Таблица 3.5

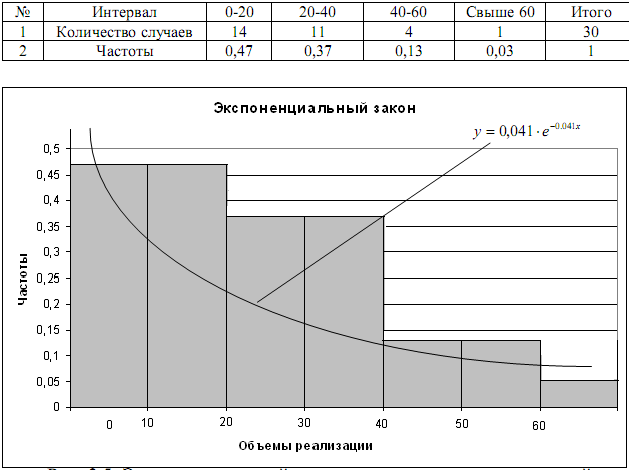
Рис. 3.5. Экспоненциальный закон распределения вероятностей

На основании полученного выражения для экспоненциального закона определяются его теоретические значения (табл. 3.6)

Таблица 3.6

Примечание: для определения теоретических частот (строка 5) значение суммы 0,038 (строка 4) принимается за единицу.

Вероятности по гипотезе нормального закона для каждого интервала определяются с помощью функции Лапласа:

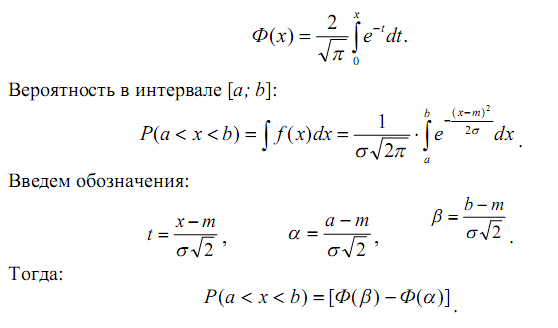
Функция Лапласа табулирована и при вычислении вероятностей конкретных значений интервалов используются ее табличные значения.

Для того чтобы проверить, насколько соответствует теоретическое распределение фактическому, необходимо использовать критерий согласия. Рассчитаем значение χ ² для экспоненциального и нормального распределений. Значение χ ², которое будет меньше, говорит о более высоком уровне соответствия данного теоретического распределения фактическому (табл. 3.7).

Таблица 3.7

Расчеты для нормального распределения:

а) рассчитываются вероятности для каждого из интервалов (с помощью табличных значений функции Лапласа):

б) рассчитываются n_т для каждого интервала:

1) 0,12 · 30 = 3,6;

2) 0,20 · 30 = 6,0;

3) 0,41 · 30 = 12,3;

4) 0,19 · 30 = 5,7;

5) 0,08 · 30 = 2,4;

6) 0,02 · 30 = 0,6.

в) рассчитываются значения 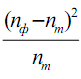для каждого интервала:

При вычислении значения χ² в качестве фактических частот (п_ф) принято количество случаев (табл. 3.4, строка 1).

Производится сравнение полученных результатов:

1. Х² = 7,86 – при экспоненциальном распределении;

2. Х² = 5,46 – при нормальном распределении; 5,46 < 7,86 следовательно, теоретическое нормальное распределение в большей степени соответствует фактическому, чем экспоненциальное.

В общем случае ряд логистических процессов, а именно: продажи, отгрузка продукции с оптово-торговых предприятий, движение запасов, оказание услуг при поставках продукции, расходование материальных ресурсов и т.п. описывается нормальным законом распределения вероятностей. Отличительным признаком такого распределения является наличие выраженной симметрии случайных величин относительно их среднего значения. Для указанных процессов нормальный закон применим для всей продукции, определенных ассортиментных групп или отдельных наименований товаров.

При АВС – анализе структуры логистических процессов, получаемые характеристики в стоимостном или натуральном выражениях подчинены экспоненциальному распределению.

Тот факт, что реализация продукции соответствует нормальному закону, имеет важное значение для логистики, поскольку позволяет определять величину товарного запаса, для чего рекомендуется следующая формула:

г де V– необходимая величина товарного запаса на определенный период;

G – средняя реализация в единицу времени (день, неделя, месяц);

Q– среднеквадратическое отклонение.

Для рассматриваемого примера товарный запас равен:

V = 24,1 + 3·14,9 = 68,8 тыс. руб.

Данная модель показывает, что любое требование покупателя на то или иное количество товара должно быть удовлетворено с вероятностью близкой к 1. В этой модели используется правило «трех сигм»: в нормальном законе 3σ соответствует вероятности 0,99.

В современных условиях компьютерные технологии позволяют отслеживать в текущем режиме времени среднюю реализацию и среднеквадратические отклонения и, соответственно, корректировать величину товарного запаса.

Предоставленная модель определения товарного запаса может быть использована как для розничной, так и для оптовой торговли.