3.1. Нормальный закон распределения вероятностей
Плотность нормального распределения имеет следующий вид:
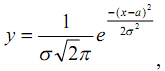
г
де
а
– центр распределения вероятностей
или математическое ожидание данной
случайной величины, т. е. а
=
М
(х);
σ- среднеквадратичное отклонение данной случайной величины.
На практике исчисляются соответствующие статистические оценки. Так, оценкой для математического ожидания будет средняя величина
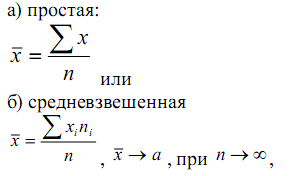
где n – количество данных в рассматриваемом статистическом массиве.
Математическое ожидание есть то теоретическое значение данной случайной величины, к которому стремится средняя величина при неограниченном увеличении количества данных.
Среднеквадратичное отклонение:
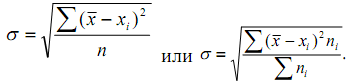
В
логистике то или иное значение величины
оценивается значением
,
при этом вычисляется коэффициент
вариации.
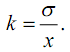
При достаточно больших количествах данных σ определяется по следующей формуле:
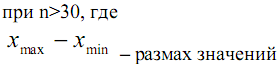
На рис. 3.1. представлен график нормального закона распределения вероятностей.
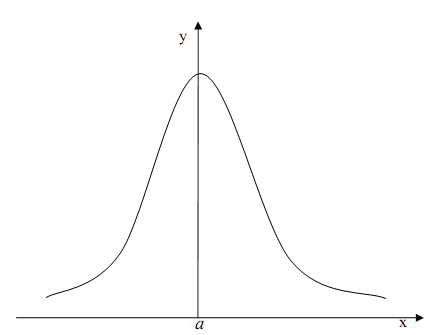
Рис. 3.1. Нормальный закон распределения вероятностей
3.2. Экспоненциальный закон распределения вероятностей
Плотность экспоненциального закона распределения вероятностей имеет следующий вид:
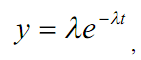
где е – основание натурального логарифма, е= 2,72… Экспоненциальный закон описывает временные параметры случайных логистических процессов. Под экспоненциальный закон подпадают следующие случайные величины:
1) время обслуживания покупателей;
2) Время погрузки-выгрузки транспортных средств;
3) время, затрачиваемое на выполнение прочих логистических операций
4) интервал между заявками, приходящими на обслуживание.
Особенностью экспоненциального закона является то, что он определяется одним параметром λ. При этом
где
- среднее значение исследуемого временного
параметра.
Для величин, подчиняющихся экспоненциальному закону, математическое ожидание М и среднеквадратичное значение равны между собой.
На рис. 3.2 представлен график экспоненциального закона.
Рис. 3.2. Экспоненциальный закон распределения вероятностей
Экспоненциальный закон описывает распределение номенклатуры продукции в зависимости от частоты её использования в производственно-коммерческой деятельности на группы А, В и С.
3.3. Биноминальный закон распределения вероятностей
Биноминальный закон распределения вероятностей выражается формулой:
Указанный закон определяет вероятности наступления m событий из общего числа событий n, где p – вероятность наступления одного события из данной группы событий;
q – вероятность ненаступления указанного события, q = 1- р.
Величина
- количество сочетаний из n
по m,
определяется по формуле:
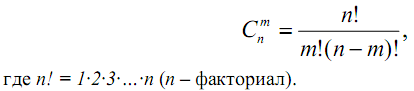
Для вычисления числа сочетаний используется равенство:
При биноминальном распределении наивероятнейшее число событий равно:
Пример: База снабжает 10 потребителей. Вероятность поступления заявки от одного потребителя р = 0,8 (q = 0,2), тогда наивероятнейшее число заявок равно: n p = 10 · 0,8 = 8 заявок. Определить вероятности поступления заявок 0, 1, 2…10.
Решение:
Определяется вероятность поступления наивероятнейшего количества заявок:
Аналогичным способом вычисляются остальные вероятности. Результаты приведены в табл. 3.1 и на рис. 3.3.
Таблица 3.1
Рис. 3.3 График распределения вероятностей Р10,m