Глава 3. Методы и модели теории вероятностей в логистике

Случайные отклонения сопутствуют любому закономерному процессу, а тем более логистическим процессам в рыночной экономике. Практика ставит такие задачи, в которых различные факторы играют существенную роль в рассматриваемых процессах, однако число этих факторов столь велико, что проследить причинно-следственные связи между ними не всегда представляется возможным. Элементы неопределенности, сложности, многопричинности присущи случайным явлениям и процессам в логистике, а поэтому требуются специальные методы для их исследования, изучения и управления. Такие методы и разрабатывает теория вероятностей. Таким образом, теория вероятностей в логистике рассматривает случайные величины, обусловленные логистическими процессами и операциями.

Так, в частности, в логистике имеют место следующие стохастические случайные величины:

1. Спрос (платежеспособность).

2. Объем реализации (объем продаж).

3. Длительность (период реализации).

4. Выручка от реализации продукции.

5. Издержки:

- общие;

- логистические;

- транзакционные.

6. Время погрузки-выгрузки транспортных средств.

7. Время доставки (перемещения продукции).

8. Уровень использования грузоподъемности и грузовместимости транспортных средств.

9. Время обслуживания покупателей (потребителей).

10. Товарооборот торгового предприятия.

11. Оборот оптово-торговой базы.

12. Поток потребителей (поток заявок на обслуживание).

13. Время занятости средств обслуживания.

14. Движение товарного запаса.

15. Объем партии отгрузки реализуемой продукции.

16. Распределение продукции по группам АВС.

17. Процесс поставки – надежность поставок и другие.

Если изучаемое явление представляется в виде полной группы событий, которые несовместимы и равновозможны, то вероятность данного события равна отношению числа m благоприятствующих этому событию случаев к общему числу n возможных случаев, т. е. вероятность равна:

На практике рассматривается статистическая вероятность, в результате накопленных статистических данных о благоприятствующих событиях m и общего числа событий n.

Так, например, в логистике используется такая величина, как надежность снабжения. Надежность снабжения в большинстве случаев величина случайная и определяется за определенный период времени как отношение числа поставок, выполненных согласно договору поставки, к общему числу поставок.

Допустим, за рассматриваемый период было выполнено поставщиком 24 поставки, из них 18 поставок соответствуют параметрам, предусмотренным договором поставки. Отсюда надежность равняется:

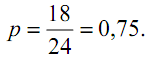
Поставка соответствующей надежности определяется следующими параметрами: количество, качество, сроки поставок.

Случайные величины характеризуются законом распределения или плотностью распределения вероятностей.

x_1, x_2, … x_n – конкретные значения, принимаемые данной величиной;

p_1, p_2, … p_n – вероятности указанных значений, при этом:

В логистике наиболее распространенными являются следующие законы распределения вероятностей: нормальное, экспоненциальное, биноминальное, Пуассона.