Коэффициент корреляции рангов Кендэла
Коэффициент Кендэла также изменяется в пределах от -1 до +1 и равен нулю при отсутствии связи между рядами рангов. Коэффициент корреляции рангов Кендэла рассчитывается по формуле:
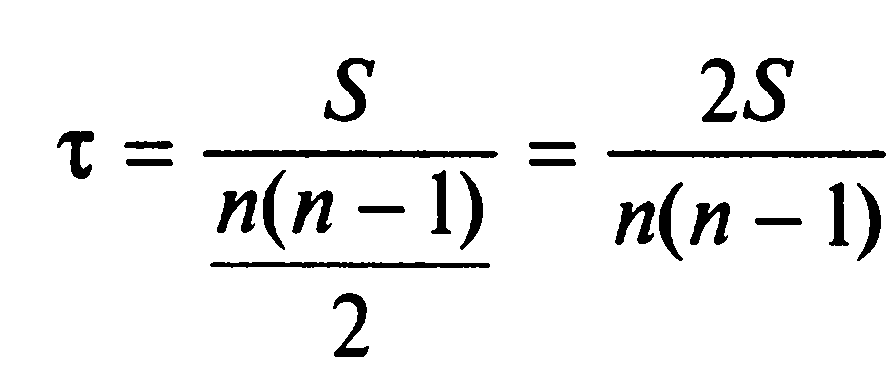
Где S = P – Q
Отсортируем по Nx:
Nx |
Ny |
P |
Q |
1 |
1 |
9 |
0 |
2 |
5 |
5 |
3 |
3 |
3 |
6 |
1 |
4 |
2 |
6 |
0 |
5 |
4 |
5 |
0 |
6 |
7 |
3 |
1 |
7 |
9 |
1 |
2 |
8 |
6 |
2 |
0 |
9 |
8 |
1 |
0 |
10 |
10 |
0 |
0 |
|
|
38 |
7 |
Получаем:
τ= |
0,688889 |
С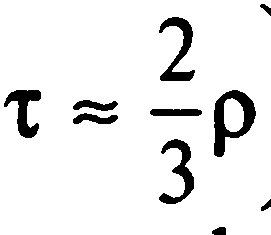
тоит
отметить, что коэффициент корреляции
рангов Кендэла всегда меньше коэффициента
корреляции рангов Спирмена и примерно
равен:
Коэффициент Фехнера
Коэффициент Фехнера основан на сравнении поведения отклонений индивидуальных значений признаков от их средней величины. Он может изменяться от -1 (обратная связь) до +1 (прямая связь). Поскольку коэффициент Фехнера зависит только от знаков и не учитывает величину самих отклонений x и y от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление.
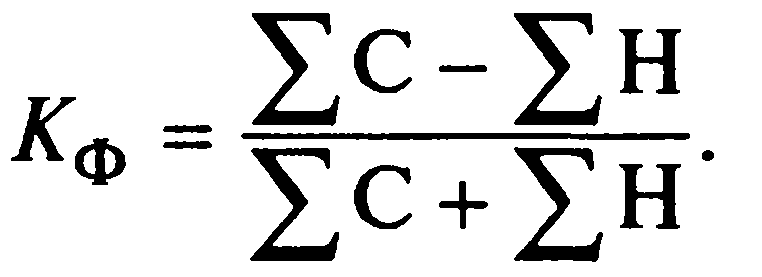
Где С – совпадение знаков, Н – несовпадение знаков.
N |
Xi-Xcp |
Yi-Ycp |
С |
Н |
1 |
16,19 |
7061,4 |
1 |
0 |
2 |
4,19 |
2632,4 |
1 |
0 |
3 |
16,19 |
3592,4 |
1 |
0 |
4 |
8,29 |
-1891,6 |
0 |
1 |
5 |
-1,41 |
-1075,6 |
1 |
0 |
6 |
-4,21 |
-2195,6 |
1 |
0 |
7 |
2,49 |
-1918,6 |
0 |
1 |
8 |
-10,41 |
-2203,6 |
1 |
0 |
9 |
-13,51 |
-1726,6 |
1 |
0 |
10 |
-17,81 |
-2274,6 |
1 |
0 |
Итого |
|
|
8 |
2 |
Получаем:
Кф= |
0,6 |
Аналитическая записка.
В данном случае имеет место прямолинейная форма корреляционной зависимости между взаимосвязанными показателями: производительность труда (факторный признак) и балансовая прибыль (результирующий признак). Уравнение регрессии имеет вид
yx= -3519,4 – 209,3939*x
Где как параметры a0 и a1, так и само уравнение являются значимыми.
Линейный коэффициент корреляции, который также является значимым, равен 0,75, что свидетельствует о наличии высокой силы связи между признаками. Коэффициент детерминации (0,57) показывает, что в 57% случаев изменение y вызвано изменением x. Остальные 43 % случаев объясняются факторами, не учтенными в модели.
Ранговые коэффициенты корреляции, такие как коэффициент корреляции рангов Спирмена (0,85) и коэффициент корреляции рангов Кендэла (0,69) также говорят нам о наличии заметной связи между показателями x и y.
Коэффициент Фехнера (0,6) показывает, что знаки большинства отклонений от средних значений по каждому признаку совпадают. Это свидетельствует о том, что связь между x и y прямая.