Значимость параметров ао и а1
Остаточная дисперсия используется для расчета средних ошибок параметров уравнения регрессии. Так, средние ошибки параметров a0 (μa0) и a1 (μa1) равны:
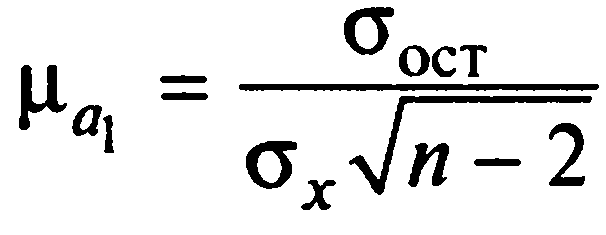
Получаем:
μa0= |
719,19465 |
μa1= |
64,468479 |
Иначе говоря
a0= -3519,4 +- 719,19
a1= 209,39 +- 64,47
Сопоставляя значение параметра с его средней ошибкой, по значению t мы можем судить о значимости данного параметра.
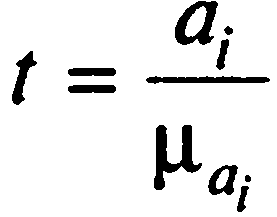
Если число наблюдений n<20, обращаемся к таблице значений t-критерия Стьюдента. Параметр считается значимым, если tфакт > tтабл.
Получаем:
ta0= |
-4,893533 |
ta1= |
3,2480049 |
tтабл= |
2,31 |
Для обоих параметров tфакт > tтабл (по модулю), а значит параметры являются значимыми
F-критерий Фишера
F-критерий Фишера помогает оценить значимость уравнения регрессии в целом. Он рассчитывается по формуле:
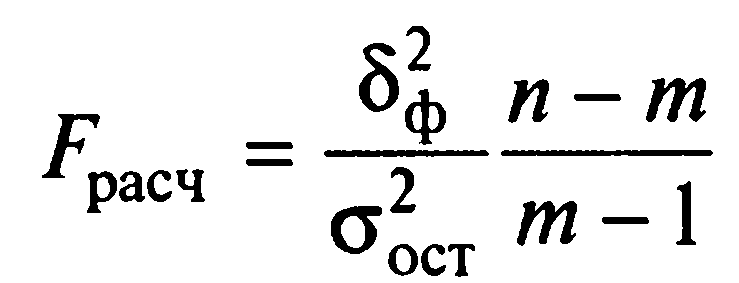
Где m – число параметров (X,Y) = 2.
Получаем:
Fрасч |
10,549536 |
Fтабл= |
5,32 |
Fрасч > Fтабл, что позволяет сделать вывод о том, что уравнение является значимым.
Ранговые коэффициенты корреляции
Коррелируются не сами значения показателей x и y, а их ранги (номера их мест в каждом ряду значений по возрастанию или убыванию).
N |
Xi |
Yi |
Nx |
Ny |
d=Nx-Ny |
d^2 |
1 |
44,4 |
9449 |
1 |
1 |
0 |
0 |
2 |
32,4 |
5020 |
3 |
3 |
0 |
0 |
3 |
44,4 |
5980 |
4 |
2 |
2 |
4 |
4 |
36,5 |
496 |
2 |
5 |
-3 |
9 |
5 |
26,8 |
1312 |
7 |
9 |
-2 |
4 |
6 |
24 |
192 |
5 |
4 |
1 |
1 |
7 |
30,7 |
469 |
6 |
7 |
-1 |
1 |
8 |
17,8 |
184 |
8 |
6 |
2 |
4 |
9 |
14,7 |
661 |
9 |
8 |
1 |
1 |
10 |
10,4 |
113 |
10 |
10 |
0 |
0 |
Итого |
282,1 |
23876 |
|
|
|
24 |
Коэффициент корреляции рангов Спирмена
Коэффициент корреляции рангов принимает значения от -1 до 1. Если ρ=1 имеет место тесная прямая связь, ρ=-1 – тесная обратная связь, ρ=0 – связь отсутствует.
Коэффициент корреляции рангов Спирмена рассчитывается по формуле:
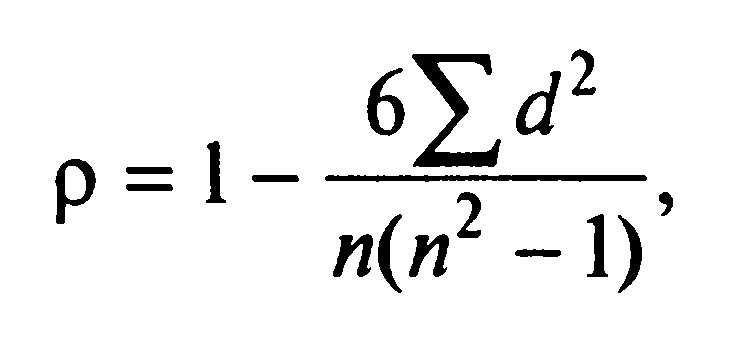
Получаем:
ρ= |
0,854545 |