33Мгу им. Ломоносова Экономичекий факультет
Самостоятельная работа по статистике
Выполнил
Студент 2 курса
академической группы Э-204
Адаменко Вячеслав
Вариант 23
N |
Xi |
Yi |
X*Y |
Xi^2 |
Yi^2 |
1 |
44,4 |
9449 |
419535,6 |
1971,36 |
89283601 |
2 |
32,4 |
5020 |
162648 |
1049,76 |
25200400 |
3 |
44,4 |
5980 |
265512 |
1971,36 |
35760400 |
4 |
36,5 |
496 |
18104 |
1332,25 |
246016 |
5 |
26,8 |
1312 |
35161,6 |
718,24 |
1721344 |
6 |
24 |
192 |
4608 |
576 |
36864 |
7 |
30,7 |
469 |
14398,3 |
942,49 |
219961 |
8 |
17,8 |
184 |
3275,2 |
316,84 |
33856 |
9 |
14,7 |
661 |
9716,7 |
216,09 |
436921 |
10 |
10,4 |
113 |
1175,2 |
108,16 |
12769 |
Итого |
282,1 |
23876 |
934134,6 |
9202,55 |
152952132 |
(Примем за данность, что между показателями существует линейная связь)
Линейная зависимость
Для нахождения а0 и а1, где а1 – коэффициент регрессии, который показывает, насколько в абсолютном выражении изменится результативный показатель y при изменении факторного показатель x на единицу, при линейной зависимости воспользуемся следующими формулами:
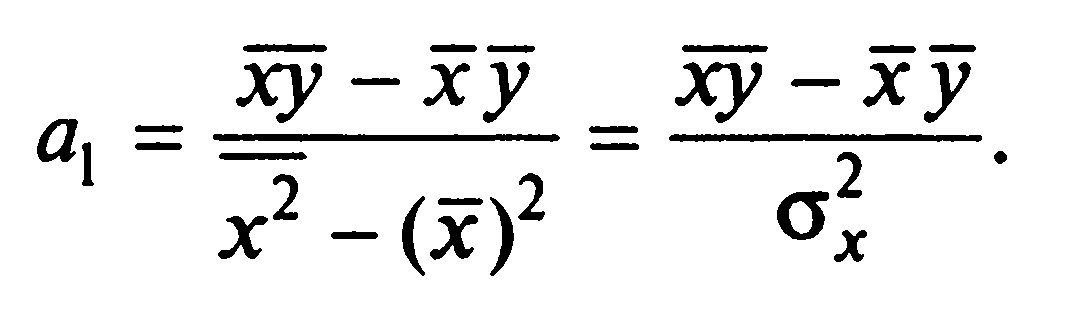
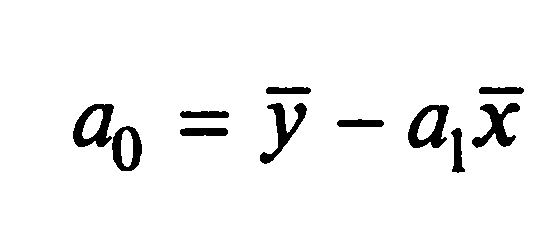
Для этого найдем дисперсии, а также средние значения в рядах xi и yi.
Xcp= |
28,21 |
Ycp= |
2387,6 |
(X*Y)cp= |
93413,46 |
σx^2= |
124,4509 |
σy^2= |
9594579 |
σx= |
11,15576 |
σy= |
3097,512 |
a1= |
209,3939 |
a0= |
-3519,4 |
Yx = -3519,4 + 209,3939*Х
Линейный коэффициент корреляции
Линейный коэффициент корреляции может принимать значения в пределах от -1 до + 1 или по модулю от 0 до 1. Чем ближе он по абсолютной величине к 1, тем теснее связь. Знак указывает направление связи: «+» - прямая зависимость, «-» имеет место при обратной зависимости.
Линейный коэффициент корреляции рассчитывается по формулам:
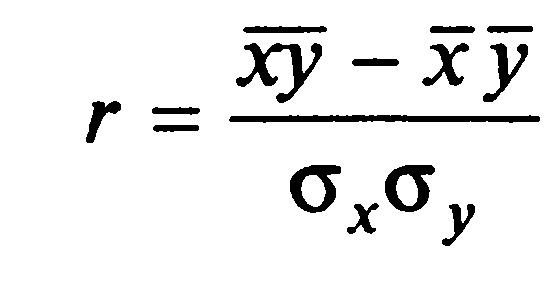
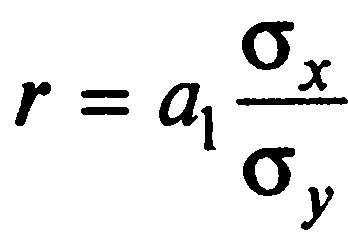
Получаем:
r= |
0,7541368 |
r(по a1)= |
0,7541368 |
При расчете коэффициента корреляции очень важно оценить его значимость. При n<30 линейный коэффициент корреляции проверяется на основе t-критерия Стьюдента. Для этого рассчитывается фактическое значение критерия (tфакт), которое сопоставляется с tтабл, определяемым по таблице значений t-критерия Стьюдента. Если tфакт > tтабл, коэффициент корреляции считается значимым, а связь реальной. Если tфакт < tтабл, то считается что связь между x и y отсутствует и значение r, отличное от нуля, получено случайно.
Средняя ошибка коэффициента корреляции рассчитывается по формуле:
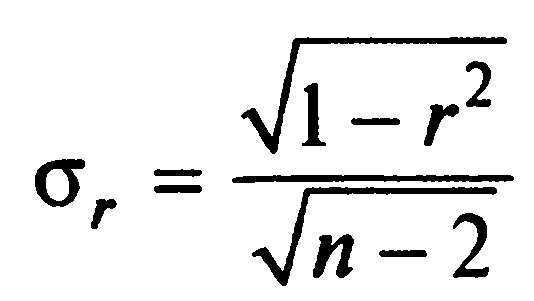
Фактическое значение критерия:
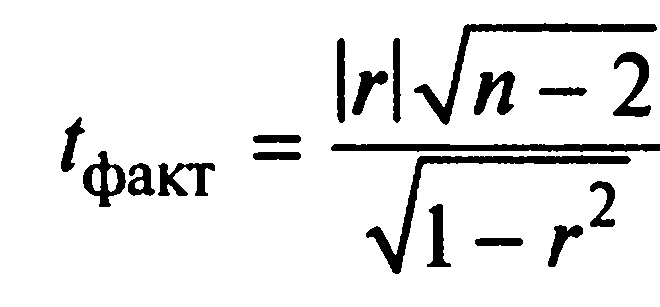
Табличное значение критерия при числе степеней свободы v = 10 – 2 = 8 и уровне значимости α = 0,05
tтабл = 2,306.
tфакт= |
3,2480049 |
σr= |
0,2321846 |
tфакт > tтабл, а значит коэффициент корреляции является значимым, а связь между x и y реальна.