
17.3 Уравновешивание механизмов
Для механизма задачи и условия уравновешивания остаются теми же, что и для звена: уменьшение инерционных нагрузок, передающихся от механизма (машины) на фундамент за счет такого распределения масс, при котором главный вектор сил инерции и главный момент сил инерции равны нулю. Первое условие определяет статическое уравновешивание, второе – моментное, а их одновременное выполнение – полное уравновешивание.
Уравновешенным называется механизм, у которого главный вектор и главный момент давления стойким на фундамент остаются постоянными при заданном движении ведущих звеньев. |
Полное
уравновешивание механизма выполняют
редко из-за его сложности. Часто
ограничиваются либо статическим
уравновешиванием, либо статическим и
уравновешиванием первой или резонансной
гармоники. Условия уравновешивания
могут иметь вид в случае статического
уравновешивания:
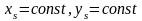 (центр масс механизма неподвижен
относительно стойки); и в случае моментного
–
(центр масс механизма неподвижен
относительно стойки); и в случае моментного
–
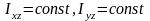 (центробежные моменты инерции должны
быть постоянны).
(центробежные моменты инерции должны
быть постоянны).
Рассмотрим примеры статического уравновешивания механизмов.
Шарнирный четырехзвенник. Воспользуемся методом замещающих масс, который заключается в следующем. Массу каждого подвижного звена по правилу рычага распределяем по концам звена и уже их уравновешиваем с помощью противовеса.
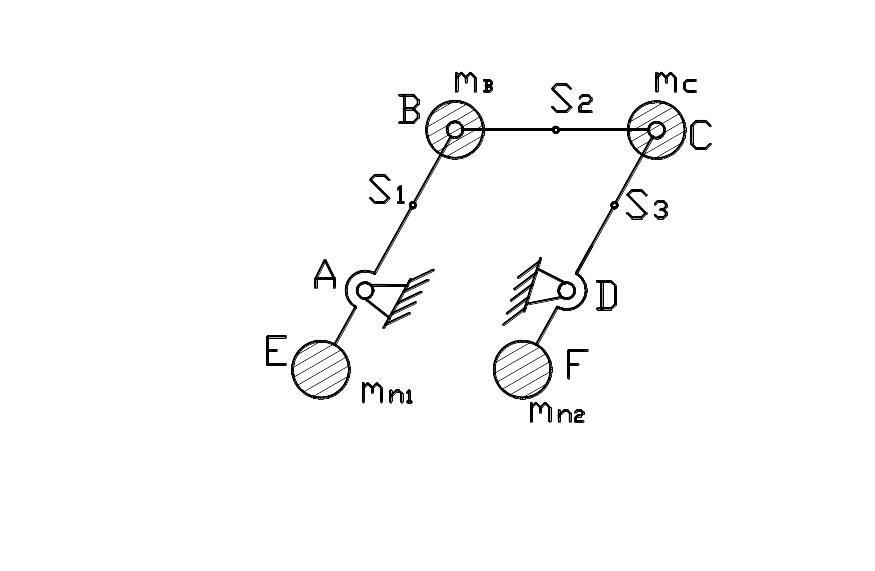
Рис.17.4 Схема уравновешивания шарнирного четырехзвенника
с помощью противовесов
На рис.17.4 масса звена 1 распределена в токи A (не показана, так как связана со стойкой и на виброактивность механизма не влияет) и B; масса звена 2 распределена в точки B и C; масса звена 3 распределена в точки C и D (не показана, как и в точке А). В результате в точке B сосредоточена масса части 1-го и 2-го звеньев; аналогично в точке С – 2-го и 3-го звеньев, которые находятся из выражений:
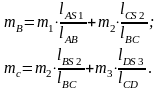
Эти массы уравновешиваются противовесами на продолжении звеньев 1 и 3. Масса противовесов находится из уравнений статики:
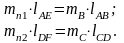
В
этих уравнениях и на рис. обозначено:
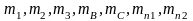 – массы 1-го, 2-го и 3-го звеньев, замещающие
массы в точках В и С, массы противовесов;.
– массы 1-го, 2-го и 3-го звеньев, замещающие
массы в точках В и С, массы противовесов;.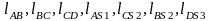 - размеры соответствующих звеньев и
отрезков.
- размеры соответствующих звеньев и
отрезков.
Здесь,
также как и при уравновешивании ротора,
неизвестных больше, чем уравнений и
необходимо задаться двумя параметрами,
например, расстояниями
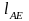 и
и
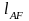 .
.
Кривошипно-шатунный механизм. Покажем несколько методов.
а). С помощью косой симметрии (рис.17.5)
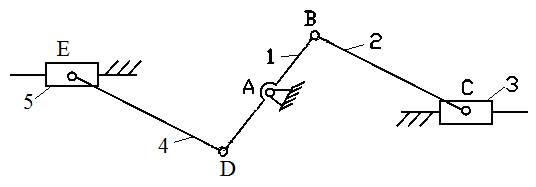
Рис.17.5 Кососимметричная схема статически уравновешенного
двухцилиндрового двигателя внутреннего сгорания
б) С помощью противовесов. Методом замещающих масс можно найти массу противовеса, устанавливаемого на продолжении шатуна ВС за точкой В, и массу противовеса, устанавливаемого на продолжении кривошипа АВ за точкой А (рис.17.6), и, тем самым, полностью статически уравновесить. Однако, противовес на шатуне заметно увеличивает габариты механизма и, поэтому, устанавливают противовес только на кривошипе, как показано на рис.17.7. В этом случае получается лишь частичное статическое уравновешивание.
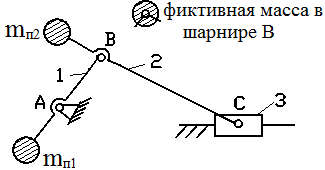
Рис.17.6 Схема уравновешивания механизма с помощью
двух противовесов
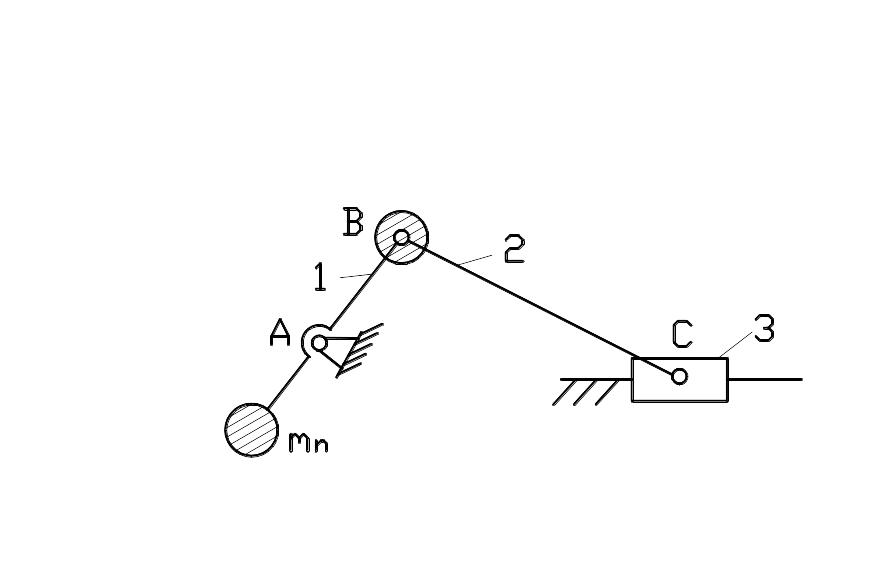
Рис.17.6 Схема уравновешивания механизма с помощью
одного противовеса
в)
С помощью зубчатых колес с противовесами.
На рис.17.8 показана принципиальная схема
уравновешивания механизма по первой
гармонике инерционного момента на
кривошипе. Массы противовесов
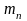 и
и
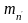
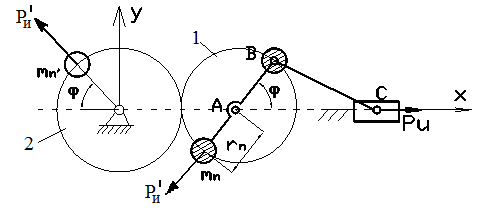
Рис.17.8 Схема уравновешивания механизма по первой гармонике
установлены
так, что создаваемые ими равные две силы
инерции
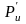 в сумме дают проекцию на ось X,
равную и противоположно направленную
силе Ри
, приложенной к ползуну, уравновешивая
ее. Проекции этих сил
на ось Y
уравновешивают друг друга. Передаточное
отношение зубчатых колес 1 и 2 равно
единице. Для уравновешивания инерционных
сил II
порядка необходимо поставить дополнительные
пары зубчатых колес с соответствующим
передаточным отношением.
в сумме дают проекцию на ось X,
равную и противоположно направленную
силе Ри
, приложенной к ползуну, уравновешивая
ее. Проекции этих сил
на ось Y
уравновешивают друг друга. Передаточное
отношение зубчатых колес 1 и 2 равно
единице. Для уравновешивания инерционных
сил II
порядка необходимо поставить дополнительные
пары зубчатых колес с соответствующим
передаточным отношением.
Можно заметить, что могут быть и другие способы уравновешивания и выбор того или иного зависит от многих факторов, например, схемы механизма, имеющегося на нем и машине места, ограничений по массе и габаритам и так далее.
