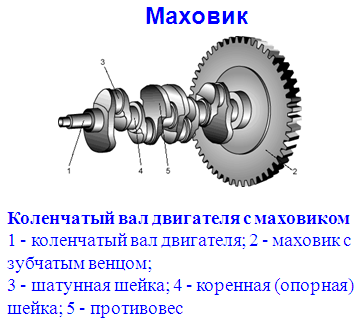
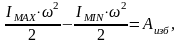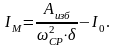ФБГОУВПО

«Московский государственный строительный университет»

кафедра «Механическое оборудование, детали машин и технология металлов»

Конспект лекции №11 по дисциплине

«Теория механизмов и машин»

для бакалавров по направлению 270800

Москва 2013-11-13

Режимы движения

Анализ движения ведут с использованием уравнения движения в той или иной форме. Воспользуемся уравнения движением в виде уравнения «живых сил»: изменение кинетической энергии равно разности работ сил движущих и сил сопротивления:

T=АдвАс

(1.2)

В соответствии с этим уравнением можно рассматривать три режима движения: разгон при ΔT>0; установившееся движение при ΔT=0; выбег или останов при ΔT<0.

На рис. показан график средней скорости движения механизма. На нем обозначено время движения при разгоне t_р, при установившемся движении t_у и при выбеге t_в. Полное время движения механизма t равно сумме времен всех трех режимов.

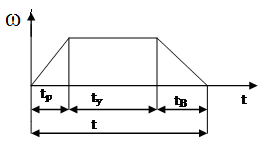
Рис. График движения механизма

16.3 Коэффициент неравномерности движения

16	Регулирование движения механизма. Неравномерность вращения ведущего звена механизма. Определение момента инерции маховика и его размеров.

Мы рассматривали график (рис. ) режимов движения звена приведения в виде прямых линий. Реально всегда существуют колебания скорости вокруг какого-то среднего значения. Эти колебания скорости часто регламентируют и для их количественной оценки служит коэффициент неравномерности движения δ, равный отношению размаха скорости к ее среднему значению. Например, для звена приведения совершающего вращательное движение:

δ=(ωmax−ωmin)/ωср,

(16.10)

где ω_max и ω_min – максимальное и минимальное значения скорости; ω_ср - среднее значение скорости: ω_ср=(ω_max+ω_min)/2.

Рис.16.1 График скорости звена приведения

в установившемся режиме

Зная коэффициент неравномерности движения δ и среднюю скорость можно найти ее допустимые наибольшие и наименьшие значения:

ωmax=ωср(1+δ/2) и ωmin=ωср(1−δ/2).

(16.11)

Следует заметить, что обычно колебания скорости коэффициентом неравномерности движения δ оценивают при установившемся режиме движения.

4. Определение момента инерции маховика

Колебания скорости звена приведения при установившемся движении могут быть периодическими и непериодическими. В случае периодических колебаний регулирование скорости можно осуществить с помощью маховика.

Маховиком называется добавочная масса вращающегося звена, предназначенная для обеспечения требуемого коэффициента неравномерности движения.

По форме маховик часто выполняют в виде массивного обода, соединенного со ступицей спицами или диском. Есть и другие формы маховика, например, в виде чечевицы, или так называемые супермаховики с навитым ободом из высокопрочной проволоки или композитных материалов. По сравнению с обычными маховиками, они могут аккумулировать больше энергии на единицу массы или обладают большей прочностью. Интересующиеся этой темой могут посмотреть работы российского ученого профессора Норберта Гулиа [ ].

Определим момент инерции маховика в первом приближении. Рассмотрим уравнение движения звена приведения на участке изменения его скорости вращения от ω_max до ω_min .

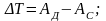
(16.12)

где 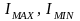- приведенный момент инерции механизма в тех его положениях, когда скорость звена приведения принимает значения соответственно ω_max и ω_min; А_изб – избыточная работа:

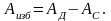
Пусть приведенный момент инерции механизма I_П состоит из постоянной части приведенного момента инерции звеньев механизма I₀ без момента инерции маховика I_М и переменной части приведенного момента инерции звеньев механизма I, величиной которой в первом приближении по сравнению с I₀и I_М можно пренебречь. Тогда

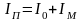
и из (16.12) получаем

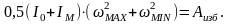
Заменим в этом выражении угловые скорости через коэффициент неравномерности движения  и среднею скорость ω_ср по (16.11) и получим формулу определения момента инерции маховика, установленного на звене приведения:

(16.12)

В формуле (16.12) неизвестна лишь избыточная работа А_изб. Она равна:

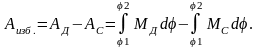
Из этой формулы следует, что избыточную работу можно найти как разность площадей под графиками моментов движущего и сопротивлений. На схеме (рис.16.2) заштрихованы три разные избыточные работы: две со знаком минус (А_Д<А_С) и одна со знаком плюс (А_Д>А_С). За цикл установившегося движения, для которого определяется значение момента инерции маховика, работа сил движущих должна быть равна работе сил сопротивления (А_Д=А_С). Поэтому сумма площадей со знаком плюс должна быть равна сумме площадей со знаком минус, то есть, F₂-F₁-F₃=0. Для каждой из избыточных площадей можно вычислить момент инерции маховика, но только для интервала угла поворота звена приведения с максимальной избыточной работой может быть найдено то значение момента инерции маховика, которое обеспечит требуемый коэффициент неравномерности движения.

С учетом масштабов построения графиков моментов движущего и сопротивления избыточная работа, подставляемая в формулу (16.12), будет равна

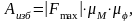
где - масштабы графика по осям ординат и абсцисс соответственно.

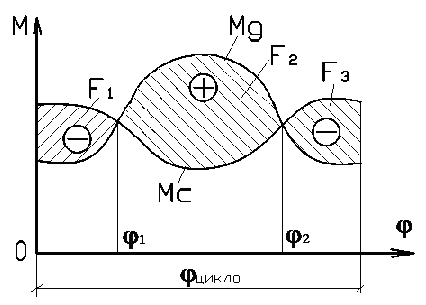
Рис.16.2 Схема к определению избыточной работы

Задача №291. Силы, приложенные к машинному агрегату, и его массы приведены к звену АВ. Движение агрегата установилось. Один цикл установившегося движения соответствует углу φ_ц = 2π. Приведенный момент сил сопротивления М_с изменяется согласно графику, а приведенный момент движущих сил М_д постоянен на всем цикле установившегося движения. Приведенный момент инерции масс звеньев машинного агрегата постоянен и равен I_п = 0,2 кгм². Средняя угловая скорость звена АВ равна ω_ср = 30 сек^-1.

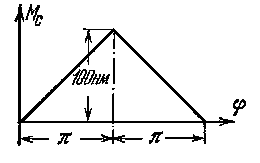
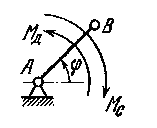
Определить, какой должна быть величина момента инерции маховика, устанавливаемого на валу А звена АВ, чтобы коэффициент неравномерности движения δ был равен 0,08.

• План решения задачи №291.

• 1. Из сравнительного анализа исходных данных и формулы определения момента инерции маховика определяются искомые параметры.

• 2. Из условия установившегося движения определяется значение движущего момента.

• 3. По графику движущего момента и момента сопротивлений находится максимальная избыточная работа.

• 4. Определяется (вычисляется) момент инерции маховика.