
Вариант 7
1. Найдите 52% от числа
2. Задача. Даны множества А={ x|x є R, 1≤x≤10}, B={x|x є R, –5<x≤6}, C={x|x є R, –4≤x<7}, D={x|x є R, –1<x≤11}. Укажите характеристические свойства множеств: а) AUB∩C;
б) A\BUC.
3. Задача. В классе 40 человек. Играют в баскетбол 26 человек, занимаются плаванием 25, ходят на лыжах 27. Одновременно занимаются плаванием и баскетболом 15, баскетболом и лыжами 16, плаванием и лыжами 18 человек. Один из учащихся освобожден от занятий по физкультуре. Сколько человек занимается всеми указанными видами спорта? Сколько человек занимается только одним видом спорта?
4. Изобразите с помощью кругов Эйлера отношения между понятиями.
Футболист, спортсмен, баскетболист, человек, россиянин.
Сторожевая собака, млекопитающее, животное, лесное животное.
5. Заштрихуйте ту часть рисунка, которая соответствует множеству, полученному в результате действий над данными множествами.
|
(В \ А) С
|
6. По предложенным схемам составьте соответствующие им выражения.
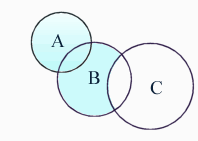
7. Найти предел функции, не используя правило Лопиталя.
![]()
8. Найти производную заданной функции.
![]()
Вычислить интеграл:
![]()
В треугольнике АВС угол С равен 90°, косинус внешнего угла при вершине А равен
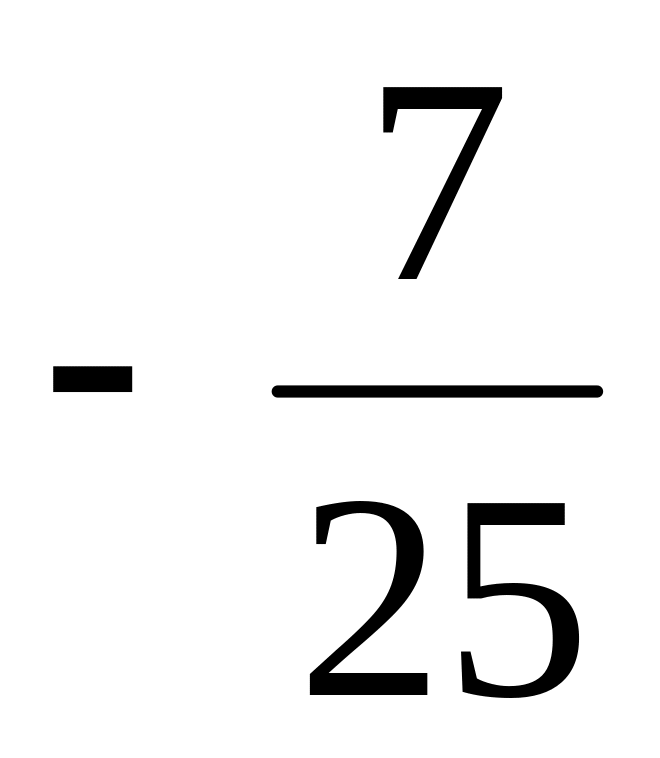 .
Найдите cosB.
.
Найдите cosB.
Вариант 8
1. Найдите 48% от числа
Задача. Даны множества А={ x|x є R, 2≤x≤10}, B={x|x є R, –4<x≤6}, C={x|x є R, –5≤x<7}, D={x|x є R, –2<x≤11}. Укажите характеристические свойства множеств: а)AUB∩D; б) A\DUC.
Задача. В школе 70 учеников. Из них 27 ходит в драмкружок, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов. 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не ходят в драмкружок?
Изобразите с помощью кругов Эйлера отношения между понятиями.
Сторожевая собака, млекопитающее, животное, лесное животное.
Книга, словарь, энциклопедия, философская энциклопедия, словарь по логике.
5. Заштрихуйте ту часть рисунка, которая соответствует множеству, полученному в результате действий над данными множествами.
|
(А \ В) (С \ В) |
6. По предложенным схемам составьте соответствующие им выражения.
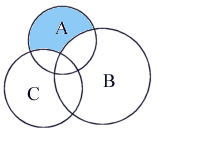
7.Найти предел функций
![]()
Найти производные заданных функций.
![]()
Вычислить интеграл:
![]()
В правильной четырехугольной пирамиде SABCD точка O – центр основания, S – вершина, SO=12, BD=18. Найдите боковое ребро SA.
