П.2 Подмножество. Основные числовые множества.

Опр.2.2.1 Множество В, состоящее из некоторых элементов данного множества А (и только из них), называется подмножеством (частью) этого множества.

Это записывается так: В А или АВ. Говорят, что «В – подмножество А» или «В содержится в А» или «А содержит В». Заметим, что m(В)  m(А).

Знак  называется знаком включения.

Отметим основные свойства отношения включения между множествами:

1. А для любого множества А;

2. АА для любого множества А (рефлексивность);

3. из того, что ВА не следует АВ (не симметричность);

4. если АВ и ВА, то А=В (антисимметричность);

5. если АВ и ВС, то АС (транзитивность).

Основные числовые множества:

N={1,2,3,4,…} – множество натуральных чисел;

Z={…,-4,-3,-2,-1,0,1,2,3,4,…} – множество целых чисел (содержит все натуральные числа и числа, им противоположные), NZ;

Q={x 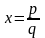 , где pZ, qN} – множество рациональных чисел (состоит из чисел, допускающих представление в виде дроби), NZQ;

R=(-∞;+∞) – множество действительных чисел, QR (кроме всех рациональных чисел, содержит иррациональные числа, содержащие в своей записи знаки радикалов: ).

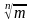П.3 Операции над множествами.

Опр.2.3.1 Пересечением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат каждому из данных множеств: С={х хА и хВ}. Обозначается, АВ.

Опр. 2.3.2 Объединением множеств А и В называется множество С, которое состоит из всех элементов данных множеств А и В и только из них: С={х хА или хВ}. Обозначается, АВ.

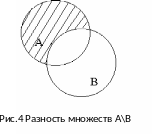
Опр.2.3.3 Разностью множеств А и В называется множество С, состоящее из всех элементов множества А, не принадлежащих множеству В: С={х  хА и хВ}. Обозначается, А\В.

В случае, когда В является подмножеством А, т.е. ВА, разность А\В называется дополнением множества В до множества А (или относительно множества А).

Опр.2.3.5 дополнением множества а называется разность u\а.. обозначается, а’ или а и читается «не-а» . иначе, дополнением множества а называется множество а’, состоящее из всех элементов, не принадлежащих множеству а.

Теперь укажем основные свойства изученных выше операций над множествами:

Свойства операции пересечения: АА=А; А=; АА’=; АU=А; АВ=ВА.	Свойства операции объединения: АА=А; А=А; АА’=U; АU=U; АВ=ВА.
Свойства операции разности: 1) А\А=; 4) А\U=; 2) А\=А; 5) U\А=А’; 3) А\А’=А; 6) \А=; 7) А\В  В\А.

П.4 Диаграммы Эйлера-Венна.

Для наглядного представления (графического изображения) множеств и результатов операций над ними удобно пользоваться так называемыми диаграммами Эйлера-Венна (кругами Эйлера).

П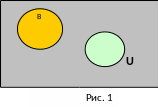 ри этом множества изображаются на плоскости в виде замкнутых кругов, а универсальное множество в виде прямоугольника. Элементы множества – точки внутри соответствующего круга.

З адачи на дом по темам данной лекции:

	Вычислить определитель. 2.Вычислить определитель:
	3.Найти произведение АВ, если , . 4.Найти произведение АВ, если , . 5.Вычислить

К теме Множества:

1. Пусть А={0;2;4;6}, B={-3;8;11}, C={-3;2;4;15;0}. Найти (АÇВ)È(СÇ(АÈВ))

2. Пусть А ={0;2;11;47} В={ 3n-2 | 0<n < 6 }. Найти АÈВ, АÇВ, А\В, В\А

3. Пусть А ={0;2;12;42} В={ 3n | 0<n<10 }. Найти АÈВ, АÇВ, А\В, В\А

4. Пусть А = { (x, y) | x2+y2 > 0}; В = {(x, y) | y > -1 } Изобразить множества АÇВ, ВÈА, А\В, В\А
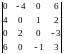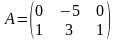
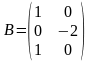