П.10.1. Построение критериев проверки гипотез о распределении случайной величины

Пусть дана случайная величина и генеральная выборка , по которой можно построить статистическую функцию распределения

Пусть по виду гистограммы выдвигается гипотеза о виде случайной величины , с функцией распределения

Возникает задача – проверить правдоподобность этой гипотезы.

На сколько могут отличаться статистическая функция распределения от гипотетической? Чем больше это расхождение, тем более маловероятна данная гипотеза и тем с большей уверенностью можно утверждать, что эта гипотеза не верна.

Чтобы построить некоторый критерий, определяющий, можно ли считать, что статистическая функция распределения и гипотетическая функция распределения совпадают, берут не разность этих функций, а некоторую функцию – это числовая функция, выбирают эту функцию такой, чтобы ее распределение было известным.

Число на выходе функции зависит от выборки, то есть эта функция случайна, следовательно, она имеет свое распределение. Надо подобрать функцию таким образом, чтобы было известно ее распределение.

Пирсон предложил критерий : ,

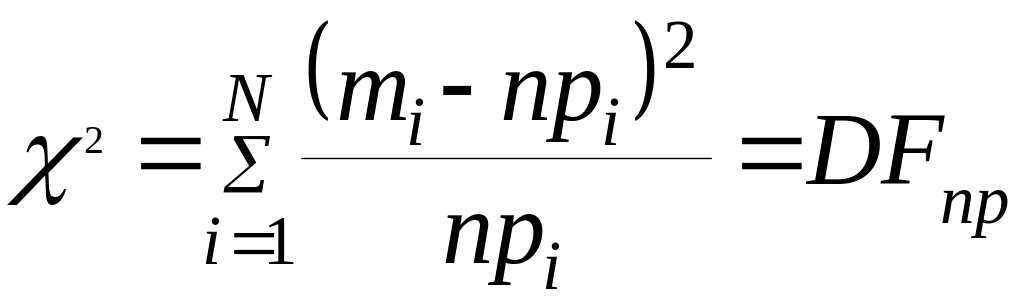здесь - конкретное число, полученное практически;

- количество интервалов;

- вероятность попасть в некоторую область ( -ый интервал);

- получение ожидаемого количества элементов выборки, которые должны попасть в -ый интервал (то есть математическое ожидание элементов выборки , которые должны попасть в -ый интервал);

- реальное количество элементов выборки, которые попали в -ый интервал;

- разница между ними.

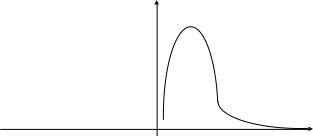
подчиняется распределению:

│

│ │

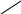Чем больше , тем больше расхождение между и , следовательно, шансы принять гипотезу уменьшаются.

Введем некоторый достаточно большой порог для и назовем его .

Все зависит от вероятности попадания в область правее - уровня значимости.

- вероятность, которая соответствует практически невозможному событию.

, то есть с вероятностью принимается гипотеза

Таким образом, в чем же состоит критерий?

Если при определении мы не попадаем в критическую зону (ту часть графика, которая левее ), то говорят, что практические данные эксперимента не противоречат гипотезе или, иначе говоря, гипотеза принимается.

Если попадает в критическую зону, то это означает, что произошло практически невозможное событие, так как слишком большое расхождение для того, чтобы эта гипотеза была верна, то есть ее принять нельзя, гипотеза отвергается.

Если известно , то по распределению можно найти вероятность того, что окажется больше :

Если вероятность , то не попадаем в некритическую зону.

Если вероятность , то попадаем в критическую зону.

Если известно , то по таблицам можно найти по

Если меньше , то тогда мы оказываемся в зоне, где можно принять гипотезу. Если наоборот, то нельзя принять.

Таким образом можно построить множество критериев для проверки условий.