11.2. Анализ обобщенных

Τ- И П-ОБРАЗНЫХ СХЕМ ФИЛЬТРОВ

Рассмотрим характеристические параметры и условия пропу­скания и задерживания реактивных симметричных Т- и П-образ­ных схем фильтров (рис. 11.2,б и в). Для удобства анализа со­противления плеч принято обозначать для Т-образного звена

а для П-образного звена — Z₁ и 2Z₂.

11.2.1. Характеристическое сопротивление

Так как рассматриваемые схемы являются симметричными че­тырехполюсниками, то для определения их характеристических сопротивлений воспользуемся выражением (10.44):

где Z_X и Z_K — сопротивления холостого хода и короткого замы­кания.

Из схемы Г-образного звена (см. рис. 11.2,6) найдем:

Подставив это в выражение для Zc, получим

Для П-образной схемы (см. рис. 11.2,в):

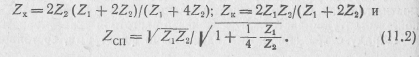
11.2.2. Характеристическая постоянная передачи

Для определения характеристической постоянной передачи рассматриваемых схем воспользуемся выраже­нием (10.57) и зависимостями между параметрами четырехпо­люсника (табл. 10.1), из которых найдем

Подставив в последнее выражение найденные выше сопротив­ления Z_x и Z_K, для обеих рассматриваемых схем получим одно и то же выражение . При этом будем иметь

При анализе фильтров вместо иногда удобнее пользовагься . Для этого воспользуемся известным из тригономет рии выражением

Учитывая (11.3), получим

11.2.3. Полосы пропускания и задерживания

Полосой пропускания чисто реактивного фильтра называют интервал частот, в пределах которого характеристическое затуха­ние α_с равно нулю, а полосой задерживания — интервал частот, где это затухание отлично от нуля. Иногда эти полосы называют характеристическими, чтобы отличить их от соответствующих по­лос, определение которых дано в начале раздела.

Учитывая, что ch jx=cosx, для полосы пропускания, в преде­лах которой α_с =0, будем иметь

Имея в виду, что cos x может изменяться в пределах , получим

или . (11.5)

Это неравенство определяет условия полосы пропускания. Его иногда называют условием «прозрачности». Из этого неравенства следует, что в полосе пропускания сопротивления Z_l и Z₂ должны

быть чисто реактивными и противоположными по знаку (х_с или x_l), причем .

Условиями полосы задерживания являются:

τ. е. полоса задерживания будет в случае, если сопротивления плеч Z₁ и Z₂ имеют одинаковые знаки, или в случае если эти со­противления имеют разные знаки, но .

Полученные неравенства (11.5) и (11.6) можно использовать для нахождения полос пропускания и задерживания графическим методом. Для этого необходимо построить на одном графике ча­стотные зависимости сопротивлений Z₁и 4Z₂.

Найдем выражения для расчета характеристических коэффи­циентов затухания и фазы в полосах пропускания и задерживания.

В полосе пропускания и .

Подставив это значение yc в выражение (11.4), получим

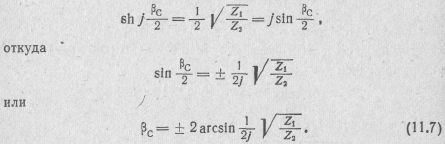
В полосе задерживания .

Подставив это выражение в формулу (11.4), получим

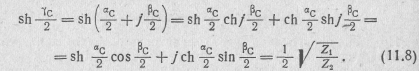
В большинстве случаев сопротивления Z₁ и Z₂ являются реак­тивными сопротивлениями противоположного знака. При этом

следовательно,

Отсюда видно, что в полосе задерживания должно выполняться равенство

Так как в рассматриваемой полосе , то из последнего ра­венства следует, что

откуда

. (11.10)

Подставив это значение в выражение (11.9), получим

Таким образом, в полосе задерживания ßα является постоян­ной величиной, равной , а определяется выражением (11.11).