Свойства матрицы рассеяния четырехполюсника установим, ис­пользуя соотношения (10.64) и (10.68). С их помощью активную мощность, рассеиваемую в четырехполюснике, выразим как

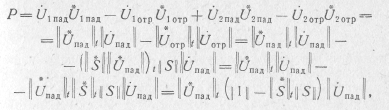
т. е.

Для всех пассивных четырехполюсников характерно, что рас­сеиваемая в них мощность Р всегда положительна. В соответствии с выражением (10.79) это возможно, если матрица ( ) является Эрмитовой и положительно полуопределенной, что справедливо для всех пассивных цепей. Используя это свойство матриц рассеяния пассивных четырехполюсников, можно дока­зать, что она существует исключительно для всех пассивных цепей.

Определив главные миноры первого порядка для Эрмитовой матрицы ( ), установим, что для пассивного четырехполюсника всегда

В четырехполюсниках без потерь, например в реактивных че­тырехполюсниках, Р=0 при любых ненулевых значениях и . Этому соответствует равенство

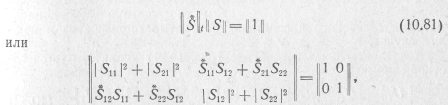
что свидетельствует о том, что матрица рассеяния четырехполюс­ника без потерь является унитарной.

¹ Как известно, Эрмитова матрица является положительно полуопределенной, если, и только если, все ее главные миноры (в том числе определитель мат­рицы) будут неотрицательны.

Равенству (10.81) одновременно соответствуют:

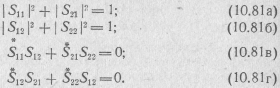
Отсюда, в частности, следует, что в четырехполюсниках без потерь невозможна полностью односторонняя передача энергии, т. е. равенство нулю одного из коэффициентов: S₂₁. или S₁₂. Дей­ствительно, если, например, S₁₂=0, то параметр S₂₁ или S₂₂ в (10.81в) также должен быть равен нулю. Но из формулы (10.816) следует, что при S₂₂=0 будет S₁₂=l, а случай S₂₁=0 при S₁₂=0 нас не интересует. Таким образом, ни один из четырехпо­люсников без потерь не может быть полностью необратимым.Од­нако |S₁₂| может быть гораздо меньше, чем |S₂₁|.

10.6. Сложные четырехполюсники

Сложными или составными называют четырехполюсники, ко­торые можно представить в виде соединения нескольких более простых четырехполюсников, параметры которых можно опреде­лить более просто. Если известны параметры составляющих четы­рехполюсников, то через них можно выразить и найти пара­метры составного сложного четы­рехполюсника.

Различают пять основных спо­собов соединения четырехполюс­ников: последовательное, парал­лельное, последовательно-парал­лельное, параллельно-последова­тельное и каскадное. Устано­вим соотношения между пара­метрами составного и составляющих четырехполюсников в каж­дом случае.

Последовательное соединение (pиc. 10.21) характеризуется со­отношениями:

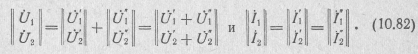
Поэтому

При последовательном соединении матрица Z-параметров сложного четырехполюсника равна сумме матриц Z-параметров составляющих его простых четырехполюсников.

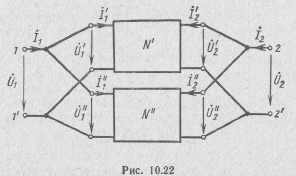
Параллельное соединение (рис. 10.22) характеризуется соотно­шениями:

При параллельном соединении матрица Y-параметров слож­ного четырехполюсника равна сумме матриц Y-параметров состав­ляющих четырехполюсников.

Последовательно-параллельное соединение (рис. 10.23) харак­теризуется, как легко убедиться, тем, что матрица H-параметров сложного четырехполюсника равна сумме H-матриц составляю­щих четырехполюсников:

(10.86)

Параллельно-последовательное соединение (рис. 10.24) ду­ально последовательно-параллельному. Нетрудно убедиться, что при нем G-матрица сложного четырехполюсника равна сумме G-матриц составляющих четырехполюсников:

(10.87)

Каскадное соединение (рис. 10.25) характеризуется соотноше­ниями:

Поэтому

т. е,

(10.89)

При каскадном соединении матрица A-параметров сложного четырехполюсника равна произведению A-матриц составляющих четырехполюсников. Перемножение матриц нужно производить

в порядке, соответствующем соединению четырехполюсников, так как оно не подчиняется переместительному закону.

Большое практическое значение имеет каскадное согласован­ное соединение n четырехполюсников с характеристическими ко­эффициентами передачи γ₁, γ₂,…, γ_n и характеристическими со-

противлениями соответственно Z_CI и Z_C2, Z_C2 и Z_C3,..,Z_Cn и Z_Cn+1 (рис. 10.26). Оно основано на согласовании характери­стических сопротивлений четырехполюсников, заключающемся в том, что входное сопротивление относительно каждой пары за­жимов любого четырехполюсника равно характеристическому. В приведенной схеме нагрузка Z_H согласована с выходным харак­теристическим сопротивлением Z_CH+1 п-го четырехполюсника, его входное сопротивление равно характеристическому Zc_n, при этом оно служит согласованной нагрузкой для (п—1)-го четырехполюс­ника и т. д. В итоге входное сопротивление первого четырехпо­люсника также равно характеристическому Z_C1.

Применительно к схеме рис. 10.26 в соответствии с форму­лой (ю.52)

, (10.90)

где

. (10.91)

Отсюда следует, что каскадное согласованное соединение п че­тырехполюсников может рассматриваться как один четырехполюс­ник, характеристические сопротивления которого равны входному характеристическому сопротивлению первого и выходному харак­теристическому сопротивлению последнего четырехполюсника. Характеристический коэффициент передачи результирующего че­тырехполюсника равен алгебраической сумме характеристических коэффициентов передачи каскадно соединенных четырехполюс­ников.