Закон сохранения энергии (уравнение Бернулли) для элементарной струйки идеальной несжимаемой жидкости.

В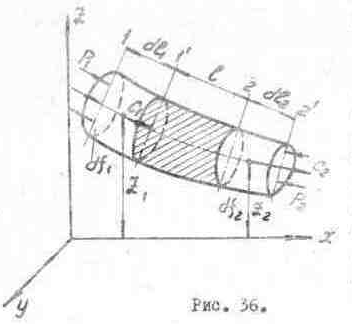 ыделим мысленно в идеальной жидкой среде элементарный объем и сформулируем для него закон сохранения энергии. Движение элемента жидкости совершается под воздействием внешних (поверхностных) и массовых сил. В процессе движения элемента жидкости изменяется его кинетическая и потенциальная энергия, а силы совершают работу. В общем случае при наличии теплообмена с окружавшей средой закон сохранения энергии гласит − изменение всех видов энергии (кинетической и внутренней) выделенного элемента жидкости за некоторый промежуток времени dt равно количеству тепла, сообщенного элементу, сложенному с работой, которую произвели за то же время приложенные к элементу внешние силы. Внешними силами являются поверхностные силы, действующие нормально к поверхности струйки, и массовые силы − силы тяжести. Рассмотрим частный случай установившегося движения идеальной несжимаемой жидкости без теплообмена с окружающей средой. Выведем уравнение сохранения энергия, называемое в этом случае уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Выделим в движущейся жидкости элементарную струйку, ограниченную сечениями 1-1, 2-2, имеющими площадь . К массе жидкости элементарной струйки применим закон сохранения энергии. За бесконечно малый промежуток времена dt выделенный объем жидкости под воздействием внешних сил переместится из положения 1-2 в положение 1'-2'. Расстояния 1-l' и 2-2' есть бесконечно малые величины. Так как движение установившееся, т.е. параметры жидкости в любой точке с течением времени не изменяются, то в заштрихованной части 1'−2, общей для обоих положений массы , изменение скорости и энергии равно нулю. Поэтому при вычислении изменения энергии массы (например, кинетической) энергия заштрихованного объема 1'-2, входящая в энергию массы , в первоначальный и конечный моменты времени, сократится, а именно

(1)

Таким образом, изменение кинетической энергии за dt сек всей массы жидкости равно разности кинетических энергий объема 2-2' вытекающей и объема 1-l' втекающей жидкости. То же относится и к изменению других видов энергии (потенциальной и энергии сил давления): при установившемся движении изменение этих видов энергии для всей массы равно разности энергии объемов 2-2' и 1-1'. Важно отметить, что в случае неустановившегося движения кинетическая энергия заштрихованного объема 1-2 в начальный и конечный моменты времени не одинакова и в уравнении, аналогичном (1), не сокращается. Так как параметры жидкости в пределах бесконечно малых объемов 1-1' и 2-2' постоянны, то индекс 1-1 заменим на 1, a 2-2 - на 2, т.е.

; ; ; .

На основании условия неразрывности течения весовой и массовый расход жидкости за одно и то же время через любое поперечное сечение элементарной струйки остается постоянным, т.е. .

Отсюда, так как

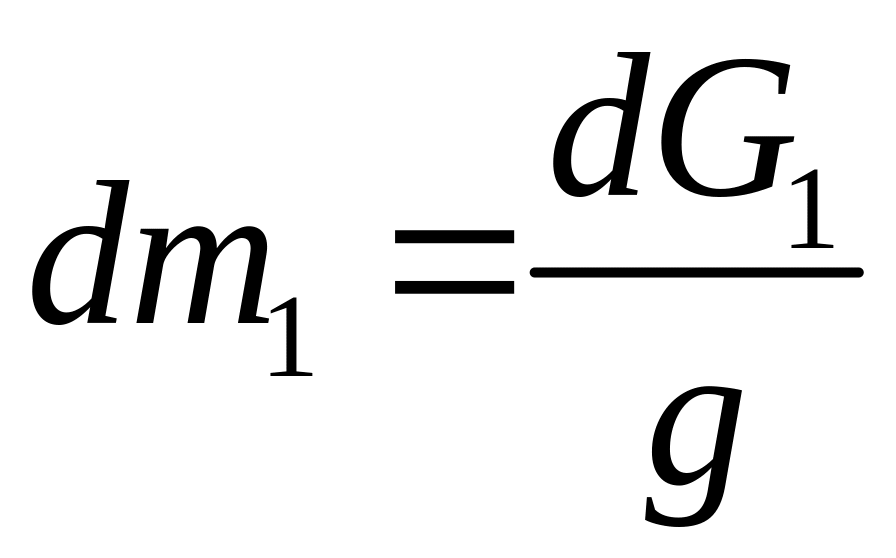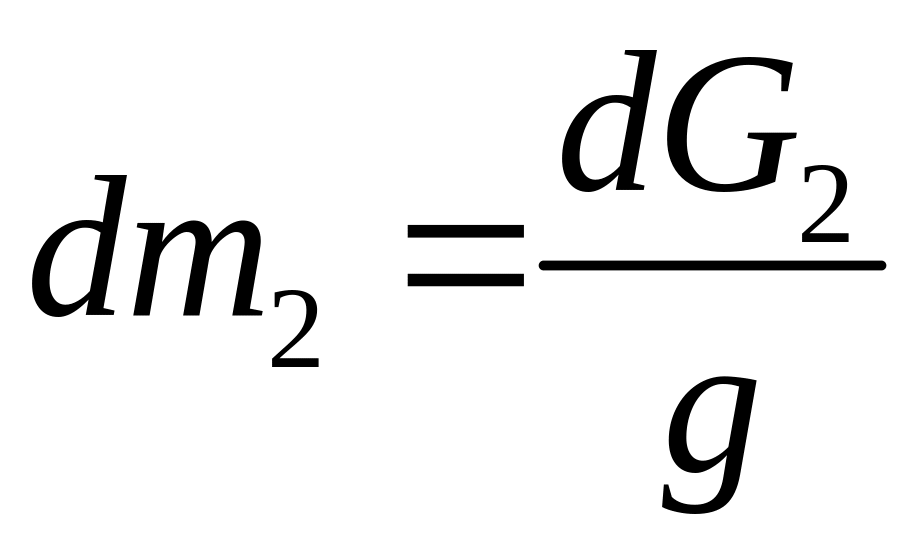и , то

При движении элемента жидкости вдоль оси элементарной струйки масса его остается постоянной, но параметры (давление, скорость) изменяются. В результате изменяются как кинетическая и потенциальная энергия, так и энергия сил давления. Подсчитаем приращение кинетической энергии рассматриваемой массы жидкости за время dt сек. На основании (1)

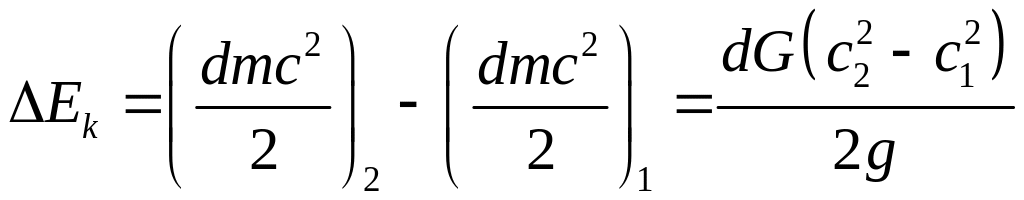
Изменение кинетической энергии движущейся массы жидкости происходит: под действием работы внешних сил, ибо внутренняя энергия несжимаемой жидкости практически не изменяется. Внешними силами в данном случае являются поверхностные силы − силы давления и массовые − силы тяжести. Подсчитаем работу сил давления и сил тяжести. Работа сил давления, приложенных к боковой поверхности струйки жидкости, равна нулю, так как эти силы перпендикулярны линиям тока, вдоль которых происходит перемещение частиц. Поэтому следует определить лишь работу сил давления, приложенных к торцам элемента. Работа , сил давления в сечении 1-1 будет положительна, так как направление силы совпадает с направлением перемещения, и выразится как произведение силы на путь , проходимый частицами жидкости за dt секунд, т.е.

.

Работа сил противодавления в сечении 2-2 отрицательна, так как направление сил противоположно направлению перемещения, и определится выражением . Итак, силы давления по всей поверхности элементарной струйки производят работу

Определим работу массовых сил, т.е. сил тяжести. Поскольку при установившемся движении работа сил тяжести заштрихованного объема не изменяется, то работа сил тяжести всей элементарной струйки за время dt будет равна работе силы тяжести жидкости объема 1-1' при перемещении ее из положения 1-1' в положение 2-2'. Иначе говоря,

где и - расстояния центров тяжести объемов 1-1' я 2-2' от некоторой горизонтальной плоскости, или иначе - ординаты центров тяжести этих объемов. Таким образом, уравнение энергии для элементарной струйки идеальной жидкости приобретает вид

. (2)

При теплообмене между струйкой и окружающей средой, в результате которого жидкость нагревается или охлаждается, в уравнение (2) справа надо ввести внешнее тепло , а слева − изменение внутренней энергии жидкости , где С − удельная теплоемкость жидкости, а − изменение температуры жидкости. После подстановки , и в (2)

.

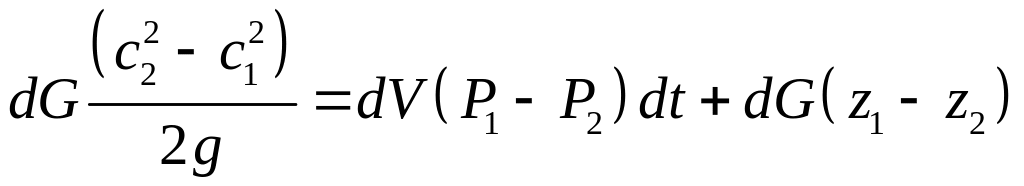Поделим на , т.е. отнесем уравнение к единице веса жидкости, тогда

.

Сгруппируем члены, относящиеся к сечению 1-1, в левой части, а относящиеся к сечению 2-2 − в правой части уравнения

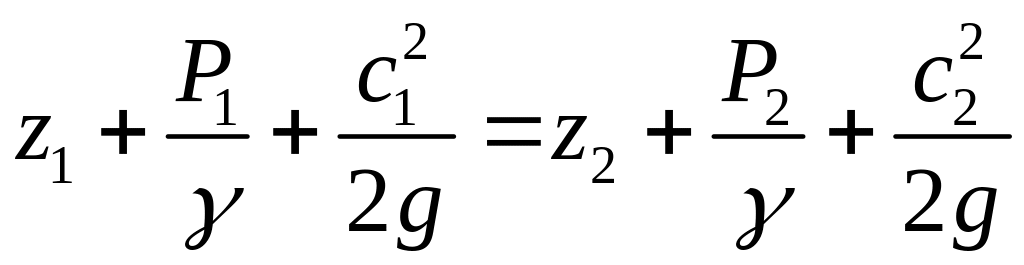. (3)

Это и есть уравнение Бернулли, написанное для элементарной струйки идеальной несжимаемой жидкости. Если неограниченно сближать между собой сечения 1-1 и 2-2, то получим уравнение Бернулли в дифференциальной форме

.

Так как сечения 1-1 и 2-2 были взяты произвольно, то уравнение Бернулли можно записать в виде

. (4)

Удельным весом жидкости называется ее вес, приходящийся на единицу объема: [кг/м³], G − вес, кг; V − объем, м³. .

Рассмотрим физический или, точнее, энергетический смысл уравнения Бернулли. Условимся называть удельной энергию, отведенную к единице веса жидкости, т.е. [кг м/кг]. Таким образом, размерность удельной анергии м. 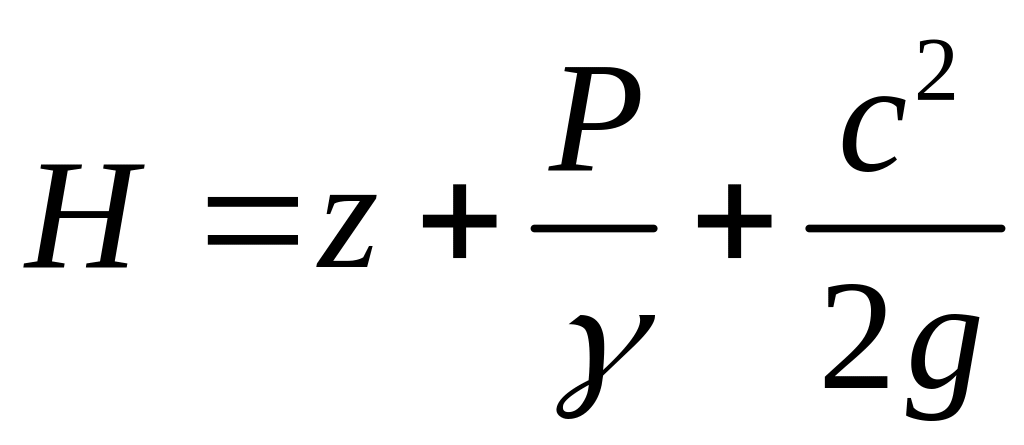Нетрудно убедиться, что члены уравнения Бернулли являются различными формами удельной механической энергии жидкости, а именно: z − удельная энергии положения, − удельная энергия сил давления, − удельная потенциальная энергия, − удельная кинетическая энергия, − полная удельная энергия. Энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки полной удельной энергии. Уравнение Бернулли представляет собой закон сохранения механической энергии при установившемся движении идеальной жидкости.