Основное дифференциальное уравнение статики жидкостей и газов.

Произведем преобразование системы дифференциальных уравнений Эйлера. Умножив каждое из уравнений соответственно на , получим:

, ,

Сложив эти уравнения, получим:

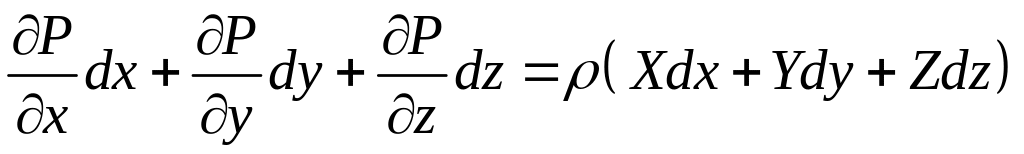
Трехчлен в левой части уравнения представляет собой полный дифференциал давления

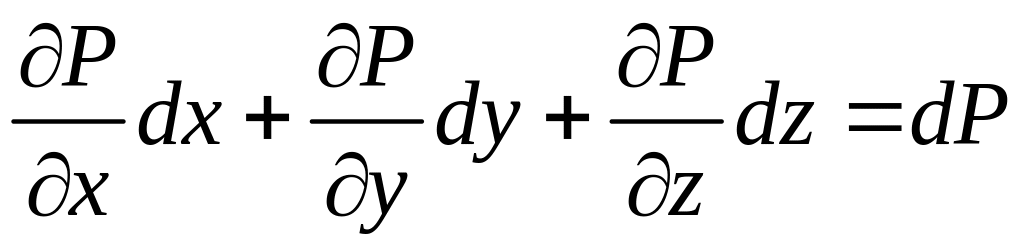
Поэтому уравнение можно записать так

(2)

Это уравнение называют основным дифференциальным уравнением статики жидкостей и газов.

В случае капельной жидкости ( ) оно легко интегрируется. В случае сжимаемой жидкости ( ) надо знать еще зависимость плотности от давления и температуры, которой может служить уравнение состояния идеального газа: .

Уравнение поверхности постоянного давления.

Составим уравнение поверхности равного давления. Так как в этом случае , следовательно . Тогда уравнение (2) примет вид:

На поверхности уровня давление и плотность постоянны, следовательно, неоднородная капельная жидкость при равновесии располагается слоями одинаковой плотности: большим значениям плотности соответствуют большие значения давлений. Поверхность уровня всегда нормальна к напряжению суммарной массовой силы, действующей на жидкость при равновесии.

Закон Паскаля.

О пределим гидростатическое давление в произвольной точке жидкости с постоянной плотностью и давлением на свободной поверхности . Для этого случая: , ;

Уравнение равновесия в дифференциальной форме примет вид: .

, , ,

или −

основное уравнение гидростатики

Выводы: Давление, с которым внешние силы действуют на граничной поверхности жидкости, передается всем частицам этой жидкости по всем направлениям без изменения величины передаваемого давления (т.е. давление жидкости не теряется в пути). Давление в любой точке складывается из давления на свободной поверхности и давления столба вышележащей жидкости. Поверхности уровня параллельны свободной поверхности .

− давление столба жидкости высотой с плотностью на площадке 1 м². z − геометрическая высота, − гидростатическое давление, Па,

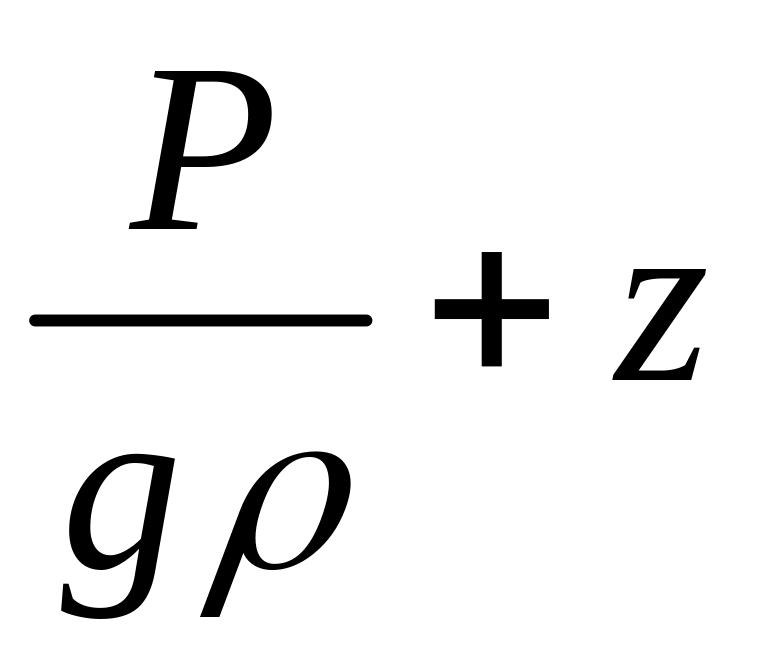− гидростатическая высота, м, − пьезометрическая высота.

Измерение давлений. Приборы для измерения давлений.

П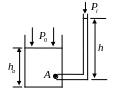 ьезометрическую высоту можно наблюдать в простейшем устройстве для измерения давления который называется пьезометром. Пьезометр − вертикальная трубка, один конец которой связан с атмосферой, а другой присоединен к объему, в котором измеряется давление. − избыточное давление, − разреженное или вакуум.

Манометр. Вакуумметр.

Параметры воздуха. МСА (международная стандартная атмосфера).

Параметры воздуха зависят от многих характеристик − высоты, широты, погоды, времени года и т.д. Такие характеристики как мощность, тяга двигателей - существенно зависят от параметров воздуха. Для сравнения характеристик при различных атмосферных условиях была принята МСА − единый, условный, закон изменения давления, температуры, плотности, которая отсчитывается от уровня океана (h=0). Общеприняты так называемые нормальные атмосферные условия: =101330 Па (760 мм.рт.ст.), =288 К (15 ), =1,23 кг/м³.

В зависимости от усредненного состава и законов изменения параметров по высоте, атмосферу принято делить на следующие условные зоны:

− тропосфера − ,

− стратосфера − ,

− химосфера − , состав газа изменяется незначительно;

− ионосфера − , содержит ионизированный газ.

При равновесии в атмосфере действует только сила тяжести, следовательно:

, , тогда дифференциальное уравнение равновесия −

, , . После преобразования получим формулы Беркеиса, для расчета параметров при изменении высоты в атмосфере:

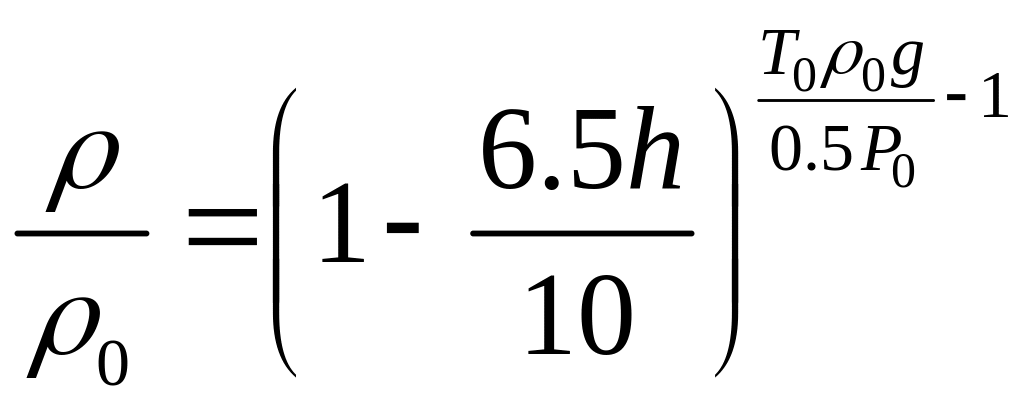, , − для тропосферы.

, − для стратосферы.

Если задана высота h, то этим по МСА, однозначно задаются параметры воздуха ( ). Если же задаются параметры, то по МСА однозначно определяются высота и недостающие параметры воздуха.

Кинематика жидкости и газа