1.3. Похибки вимірювання

Якість результатів вимірювання (РВ) та засобів вимірювання (ЗВ) прийнято характеризувати показом їх похибок. У загальному, похибка вимірювання – це критерій якості проведеного вимірювання і, являє собою відхилення результату вимірювання ФВ від її істинного значення. Поняття похибки використовується для оцінки характеристик як ЗВ так і РВ. Потрібно відрізняти похибку засобу вимірювання та похибку результату вимірювання.

Похибка результату вимірювання Δ_рв - це число, яке показує можливі межі невизначеності значення вимірюваної ФВ, тобто, Δ_рв оцінює відхилення результату Х_вим вимірювання ФВ певним ЗВ від її істинного Q_іст чи дійсного Q_дійс значення в об'єкті.

Похибка засобу вимiрювання Δ_зв - це властивість ЗВ, вимірювати ФВ з наперед заданою межею невизначеності, і для визначення цієї властивості у ЗВ необхiдно попередньо провести його метрологічні дослідження, використовуючи вiдповiднi правила метрологічної повірки або атестації.

За способом числового вираження розрізняють два види похибок: абсолютні та відносні, а також різновид відносних - приведені.

Абсолютною похибкою вимірювання ΔХ називається рiзниця мiж результатом вимiрювання (показом приладу) Х_вим та iстинним (дійсним) значенням Q_іст вимірюваної величини («виміряне мінус істинне») i надається в одиницях вимірюваної величини:

ΔX = Х_вим – Q_іст = Х_вим - Q_дійс. (1.2)

Так як істинне значення Q_іст вимірюваної величини не відоме, то не відома й похибка вимiрювання. Тому для одержання, хоча б приблизних відомостей про неї у формулу (1.2) підставляють Q_дійс вимірюваної величини.

Абсолютна похибка не може в повній мірі використовуватись як показник точності проведеного вимірювання, так як одне й теж її значення, наприклад, ΔX = 0,05мм при Q_дійс = 100мм – відповідає відносно високій точності

вимірювання, а в другому випадку при Q_дійс = 1мм – низькій.

Для більш наглядної оцінки точності проведеного вимірювання, введене

поняття відносної похибки. Відносною похибкою (γ_s) вимірювання називається похибка, яка визначається як відношення абсолютної похибки вимірювання до iстинного Q_іст чи дiйсного Q_дійс значення вимiрюваної

величини i подається у вiдсотках (%) або в долях одиниці:

γ_s = (Δ / Q_дійс) ּ 100% = [(Х_вим - Q_іст) / Q_іст] ּ 100% =

= [(Х_вим - Q_дійс) / Q_дійс] ּ 100%. (1.3)

При використовуванні поняття γ_s для розглянутого вище випадку, високій точності вимірювання відповідає мале значення відносної похибки:

γ_s = (0,05/100) ∙ 100% = 0,05%, а низькій – велике: γ_s = (0,05/1) ∙ 100% = 5%.

Але і така наглядна характеристика точності РВ не завжди придатна, наприклад, для нормування похибок ЗВ, так як дійсне значення вимірюваної величини по діапазону його вимірювання (у цьому випадку це значення міри, що приведене до взаємодії з ЗВ при його метрологічній атестації) може дорівнювати нулю. Характер зміни γ_s по діапазону вимірювання у відповідності із залежністю (1.3) має вигляд гіперболи (γ_s приймає значення безмежності на початку діапазону ЗВ, а найменше значення - в його кінці).

У зв’язку із цим, для показу й нормування похибок ЗВ, використовується різновид відносної похибки – приведена похибка (γ_пр).

Приведеною похибкою (вона відноситься тільки до ЗВ) γ_пр називається

вiдношення абсолютної похибки до розмаху N шкали ЗВ (або до його діапазону D вимірювання), яке виражене у вiдсотках (може бути виражене і в долях одиниці):

γ_пр = (Δ / N) ּ 100% = (Δ / D) ּ 100%. (1.4)

При постійній абсолютній похибці по діапазону вимірювання, приведена похибка теж постійна й дорівнює відносній похибці в кінці діапазону.

• За закономірностями прояву розрізняють:

• Випадкову складова похибки (ВСП) Δв- це складова похибки вимiрювань, яка змінюється за повторних вимiрювань однiєi i тiєiж величини ФВ випадковим чином, і в появі різних значень якої не вдається визначити будь-яку закономірність. ВСП - це похибка, яка непередбачувана ні по знаку, ні по розміру, або недостатньо вивчена.

• ВСП визначаються сукупністю причин, які важко проаналізувати. Чинники, які визивають ВСП, з’являються нерегулярно i зникають несподівано, або проявляються з непередбачуваною інтенсивністю.

• Присутність ВСП легко визначається при повторних вимiрах незмінної ФВ і проявляється у вигляді деякого розкиду результатів вимiрювань.

• Систематичну складову похибки (ССП) Δc - це складова загальної похибки, яка залишається постійною або закономірно змінюється при повторних вимiрюваннях однієї i тiє ж фізичної величини.

• До чинників першого виду, якi обумовлюють появу систематичних похибок належать: 1) неправильне градуювання ЗВ; 2) змiщення нуля ЗВ (приладу).

• Прикладом другого виду систематичних похибок – є більшість додаткових похибок, які є незмінними в часі функціями різних факторів (температури навколишнього середовища, напруги живлення, вологості і т. п..

• Прикладом систематичної похибки є, наприклад, похибка термоелектричного термометра, що закономірно змінюється внаслідок зміни температури вільних кінців термопари.

• За наявністю бо відсутністю функціонального між похибкою вимірювання та значенням вимірюваної величини розрізняють адитивну та мультиплікативну складові похибок вимірювання. Ці терміни служать опису смуги похибок ЗВ.

Адитивна (Δ_а або Δ0) (від лат. additivus – додавання) – це похибка,значення якої не залежить від вимiрюваної величини (похибка додавання до нуля).

Адитивна похибка має стале значення по всій характеристиці перетворення

ЗВ або по всій шкалі приладу. Це поняття однаково використовується як для систематичних похибок так і для випадкових.

Прикладом систематичної адитивної похибки Δ0 є неточність налаштування приладу на нуль, тобто, похибка змiщення нуля приладу, яка приводить до

Δм

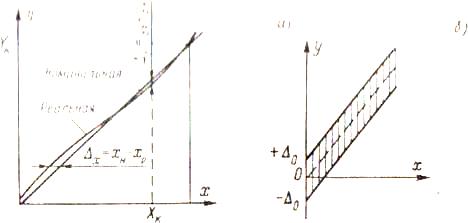
того, що реальна статична характеристика приладу зміщується по відношення до його номінальної характеристики на величину (тільки + або - ) систематичної адитивної похибки Δ0.

• У разі суто адитивної смуги похибок абсолютна похибка вимірювань Δа по діапазону вимірювання приладу залишається незмінною для будь-яких значень вимірюваної фізичної величини.

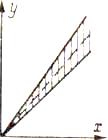
Мультиплікативна (Δм) (від лат. multiplicatio – множення) – це похибка, яка прямо пропорційно залежить від значення вимiрюваної величини (її ще називають похибкою чутливості і вона теж може бути випадковою або систематичною.

• Причини виникнення Δм – зміна чутливості ЗВ, що зв’язана зі зміною, наприклад, коефіцієнта підсилення підсилювача, або зі зміною жорсткості мембрани чутливого елемента манометра, або протидіючої пружини електромеханічного приладу.

• Оскільки в разі суто мультиплікативної смуги похибок абсолютна похибка Δм вимірювань збільшується пропорційно поточному значенню Х вимірюваної ФВ, то відносна похибка є постійною за будь-якого значення Х вимірюваної величини.

Для того, щоб орієнтуватись у метрологічних характеристиках конкретного ЗВ, щоб завчасно оцінити похибку, яку внесе даний ЗВ в кінцевий результат вимірювання, використовують так звані нормовані значення похибки ЗВ.

Під нормованим значенням похибки засобу вимірювання розуміється граничне значення похибки для даного ЗВ у відповідності з його класом точності.

Нормуються основна та додаткові похибки ЗВ. Тільки границі (межі)

основної похибки, а також коефіцієнти впливу додаткових похибок і заносять

в паспорт кожного ЗВ. Правила, у відповідності з якими назначаються ці межі, або кажуть процедура нормування похибки ЗВ, грунтується на системі стандартів, які забезпечують єдність вимірювання.

Основна похибка ЗВ (Δ₀) – це похибка ЗВ при нормальних умовах його

використовування. Вона визначається внаслідок проведення метрологічних випробовувань ЗВ в нормальних умовах, під якими при експлуатації ЗВ розуміється наступні загально прийняті умови:

■ напруга мережі живлення - (220 ) В;

■ температура навколишнього середовища – (20 2)С;

■ відносна вологість – від 30 до 80 відсотків;

■ тиск – (760 25) мм рт. ст. (101325 Па);

■ відсутність зовнішніх електричного та магнітного полів, крім земного.

Основна похибка ЗВ може надаватись як абсолютною ∆_О, так і приведеною γ_пр.

Клас точності ЗВ – це його загальна характеристика, яка визначає значення

максимальної допустимої приведеної похибки ЗВ в указаному для нього

діапазоні та гарантовані межі значення основної і додаткових похибок ЗВ.

Клас точності ЗВ визначається найбільшим значенням основної приведеної похибки ЗВ по діапазону вимірювання, яка визначена при проведенні метрологічних досліджень ЗВ та відповідним чином округлена до більшого із ряду: 6-4-2,5-2,0-1,5-1,0-0,5-0,2-0,1-0,05-0,02-0,01-0,005-0,002-0,001 і т.д.. Значення класу точності наносять на шкалу приладу.

Відповідність похибки ЗВ, присвоєному йому класу точності за час експлуатації, провіряється при періодичних повірках.

Основні способи встановлення граничних значень допустимих похибок і позначення класів точності ЗВ регламентується відповідним стандартом .

Похибка засобів вимірювання Δ_зв описується певною математичною моделлю. У загальному випадку при багаторазових вимірюваннях математичну модель абсолютної похибки Δ вимірювання надають у вигляді декількох складових, а в мінімумі - як суму двох складових, які розрізняються за закономірностями прояву:

Δ = Δ_с + Δ_в , (1.5)

де Δ_с систематична та Δ_в випадкова складові похибки.

Кожна із цих складових обумовлена дією різних чинників і може складатись у свою чергу ще з декількох складових. При такому додаванні Δ_в повинна бути визначена як довірча межа інтервалу невизначеності і відповідати

певній довірчій ймовірності.

Випадкова складова похибки (ВСП) Δ_в - це складова загальної похибки вимiрювань, яка змінюється за повторних вимiрювань одного i того ж значення ФВ випадковим чином і в появі різних значень якої (і по знаку, і по розміру) не вдається визначити будь-яку закономірність.

Під систематичною складовою похибки (ССП) Δ_c розуміється складова загальної похибки, яка залишається постійною або закономірно змінюється за повторних вимiрювань одного i того ж значення ФВ і, як правило, вона може бути усунена введенням поправки із зворотним знаком.

Для визначення ССП та ВСП проводяться перевірення або метрологічна атестації ЗВ, при яких виконуються (як правило) багаторазові вимірювання значення Х_0і зразкової міри, що приводиться до взаємодії з ЗВ. Можуть в якості дійсного значення Q_дійс вимірюваної по діапазону фізичної величини використовуватись покази зразкового ЗВ більш високого класу точності.

Отримавши ряд n результатів вимірювання X₁, X₂, X₃, ... X_n (загалом прийнято, щоб їх було не менше 20), для визначення систематичної складової похибки Δ_с, необхідно обчислити найвірогідніше значення результату вимірювання даної вибірки, вирахувавши математичне сподівання M[X] або середнє арифметичне за формулою:

M[X] = ( X_і)/n =(1/n) (X₁+X₂+X₃+...+X_n), (1.6)

та вирахувати ССП ЗВ за формулою:

Δ_с = – Х_0і . (1.7)

Таким чином, відхилення середнього значення вимірюваної величини (значення зразкової міри, що подається на вхід ЗВ) від її дійсного (істинного) значення (для цього випадку Q_дійс = Х_0і ), характеризує ССП. ССП щe

називають середньою арифметичною похибкою, або середнім арифметичним

відхиленням.

Засіб вимірювання, наприклад, інформаційно-вимірювальна система, може мати декілька складових ССП, тому для оцінки результуючої ССП .всі складові додаються алгебраїчно з урахування знаку:

= . (1.8)

Враховуючи, що точність зразкового ЗВ або міри теж має кінцеве значення, яке визначається їх класом точності, поправка на систематичну складову похибки, яка визначена за допомогою останніх, теж буде мати якусь додаткову похибку з будь-яким знак та з рівною ймовірністю. Таку додаткову похибку називають не усуненим залишком ССП .

При оцінюванні схеми вимірювання можуть бути виявлені декілька .

У загальному випадку, рахуючи не усунені залишки складової систематичної похибки взаємонезалежними, використовують для визначення сумарної систематичної похибки формулу геометричного додавання, як для випадкових похибок. Формула сумарної систематичної похибки за геометричного додавання не усунених залишків систематичної складової похибки має вигляд:

;. (1.9)

при цьому враховують, що систематичні похибки в повній мірі визначаються випадковими причинами, і для їх урахування вводять поправочний коефіцієнт , який залежить від довірчої ймовірності і декілька значень якого приведені у таблиці нижче:

	0,9	0,95	0,98	0,99
	0,95	1,1	1,3	1,4

При визначення ВСП використовують математичний апарат теорії ймовірності та поняття законів розподілу ВСП, як випадкової величини. При цьому, для практичних розрахунків ВСП використовують тільки основні числові характеристики цих законів розподілу, до яких відноситься середньоквадратичне відхилення (СКВ) σ_х розсіювання окремих результатів Х_і вимірювання відносно середнього .

При метрологічних дослідженнях в залежності від кількості n проведених вимірювань використовують різні формули для визначення СКВ ВСП, які залежать від закону її розподілу.

Для попередньої оцінки закону розподілу ВСП використовуються різні критерії, одним із яких є відносна величина середнього квадратичного відхилення – коефіцієнт варіації або у відсотках .

Якщо коефіцієнт варіації має значення 0,33...0,35, то можна рахувати, що розподіл ВСП підпорядкований нормальному закону.

Для нормального закону розподілу ВСП, який, як правило, має місце при великій кількості проведених вимірювань (n ≥ 20÷30), σ_х дорівнює:

σ_х= (при n ≥ 20÷30), (1.10)

а абсолютна ВСП Δ_р , яка відповідає довірчому інтервалу з заданою довірчою ймовірністю Р_д (індекс при Р показує вибрану довірчу ймовірність Р_д з якою проведена оцінки похибки), визначається за формулою:

Δ_р = t_н (σ_х ) = t_н σ , (1.11)

де t_н - коефіцієнт (нормована квантіль) для заданої довірчої ймовірності Р_д, який вибирають із довідника по метрології для конкретного числа n; а σ .- це дослідне середньоквадратичне відхилення при великій кількості проведених вимірювань: σ = σ_х (1.12)

При малій кількості n проведених вимірювань (2<n<20÷30) для розрахунку ВСП використовують формулу:

Δ_р = t_p(S_х ) = t_p , (1.13)

де S_х – теж СКВ σ_х, але для малої кількості проведених вимірювань, його зображують як S_х, і розраховують за формулою:

S_х = , (1.14)

а - це дослідне середньоквадратичне відхилення при малій кількості проведених вимірювань: , (1.15)

і t_р - коефіцієнт Стьюдента, значення кого в залежності від кількості проведених вимірювань n та заданою довірчою ймовірністю Р_д вибирають із метрологічних таблиць.

Вирахувана оцінка СКВ S_х при малій кількості n вимірювань є тільки деяким наближенням до істинного значення СКВ σ_х. Не можна використовува-

ти формули 1.10 та 1.11 при малій кількості n < 20,.а визначений довірчий інтервал похибки за формулами 1.13 та 1.14 з заданною ймовірністю Р_д, є тим більш ненадійним, чим менше число спостережень n. В тих випадках, коли закон розподілу не є нормальним, інколи все ж таки використовують з деяким наближенням розподіл Стьюдента для оцінки довірчого інтервалу ВСП, але степінь цього наближення залишається невідомою.

Визначення похибки засобу вимiрювань Δ_зв :

Якщо варіація відсутня або нею можна нехтувати, то основна абсолютна похибка ЗВ (при нормальних умовах його використовування), яка зображується в цьому випадку як Δ₀, в кожній точці його характеристики перетворення визначається за формулами:

■ при малому числі n дослідів (n<20): Δ₀ = |Δ_с| + t_p(S_х ); (1.16)

■ при великому числі n дослідів (n ≥ 20÷30): Δ₀ = |Δ_с| + t_н(σ_х ). (1.17)

Результатом метрологічних досліджень (атестації) нестандартних ЗВ – є теж визначення максимальної Δ_0max із основних абсолютних Δ₀ похибок ЗВ в діапазоні вимірювання D, які для всіх точок по діапазону (в спрощеному вигляді при відсутності варіації та довірчій ймовірності Р_д = 0,95) вираховують за формулою:

Δ₀ = |Δ_с | + 2 ּσ_х , (1.18)

де σ_х – середньоквадратичне відхилення ВСП.

При наявності варіації основну абсолютну похибку ЗВ в усіх точках характеристики перетворення по діапазону вимірювань визначають по формулі:

,

де g_max - коефіцієнт, який для цифрових приладів дорівнює: g_max = 2;

0,28 - це залежність, яка виражає для цифрових вимірювальних пристроїв

їх варіацію через середньо квадратичне точкове відхилення σ_н цієї варіації: σ_н = 0,28 .

Після отримання значення основної абсолютної похибки по всім точкам характеристики ЗВ, вибирають із них максимальну Δ_0max по діапазону вимірювання D (або розмаху шкали N ) і визначають максимальну приведену γ_пр.max похибку ЗВ в цьому діапазоні:

γ_пр.max = (Δ_0max / D) ∙100%= (Δ_0max / N) ∙100%. (1.19)

Така основна приведена γ_пр.max похибка ЗВ, після округлення до більшого із ряду: 6-4-2,5-2,0-1,5-1,0-0,5-0,2-0,1-0,05-0,02-0,01-0,005-0,002-0,001 і т.д., визначає його клас точності, який наносять на шкалу ЗВ.

Додаткові похибки – це похибки, які виникають при відхиленні умов використовування ЗВ від нормальних і нормуються, показуванням впливу зміни окремого фактору на зміну показів ЗВ, у вигляді певного коефіцієнта або відсотка від основної похибки. Наприклад, при зміні при зміні напруги живлення в межах +10 та -15 відсотків від номінального значення 220 В, додаткова похибка не повинна перевищувати 0,15 основної приведеної γ_пр.

У загальному вигляді сумарна (експлуатаційна) абсолютна похибка ∆ засобу вимірювання з урахуванням факторів, що впливають на ЗВ, дорівнює:

∆ = Δ₀ + , (1.20)

де Δ₀ - основна абсолютна похибка ЗВ при нормальних умовах;

Δ_і - додаткові похибки, які визиваються зміною і-го фактору, що впливає на ЗВ.

Експлуатаційна похибка ЗВ – це похибка в реальних умовах використовування ЗВ і складається із його основної похибки та всіх додаткових похибок. Вона може бути набагато більшою за основну похибку, так як додаткові похибки відповідним чином додаються до основної (формула 1.18). Всі складові експлуатаційної похибки оговорюються в технічній документації на ЗВ і визначаються при його метрологічних випробовуваннях, по розробленим у відповідності із стандартами методикам.

В техніці вимірювань використовують поняття допустимої основної похибки ЗВ, яка дозволяє проводити вимірювання за допомогою конкретного ЗВ з наперед заданою і очікуваною точністю. Допустима основна похибка ЗВ - це найбільша похибка результатів вимірювання даним ЗВ, яка допустима стандартом для його класу точності.

Запис кінцевого РВ за багаторазових вимірювань.

Визначена за формулами 1.11 або 1.13 випадкова складова похибки є похибкою Δ_рв результату вимірювання і дає змогу записати кінцевий результат вимірювання фізичної величини певним ЗВ за багаторазових вимірювань. В цьому випадку математичне сподівання M[X] або середнє арифметичне показує на найбільш вірогідне дійсне значення Q_дійс. Запис кінцевого результату вимірювання має сенс тільки тоді, коли указана похибка Δ_рв, з якою вимірювання проведені і яка повинна бути відповідним чином округлена. При цьому використовуються наступні формули:

■ при n <20: Q_дійс. = M[X] ± t_p(S_х ) ≈ ± t_p ; (1.21)

■ при n ≥ 20÷30): Q_дійс.= M[X] ± t_н(σ_х ) ≈ ± t_н σ ; (1.22).