Варіанти значень для домашнього завдання № 3 (гр..Акс-2):

№	D	К	ХВ	γS %	Rм20Ом	Rл Ом	ТСПRнест Ом	tо1 С	tо2 С	tе С	Rл0 Ом	d мм
1	0÷265	1,5	247,5	1,5	249,5	5,25	432,5	325	125	65,5	7,5	0,12
2	0÷245	3,0	237,5	2,5	314,5	6,45	617,5	345	115	57,5	10,0	0,13
3	0÷255	1,5	238,5	2,0	295,5	4,15	427,5	315	130	45,6	5,0	0,36
4	0÷285	2,5	277,5	0,5	346,5	4,55	447,5	345	140	47,8	7,5	0,24
5	0÷325	1,5	323,5	1,5	354,5	5,15	532,5	325	105	58,9	7,5	0,27
6	0÷345	2,5	333,5	2,5	364,5	8,2	576,5	270	105	55,5	10,0	0,15
7	0÷315	1,5	293,5	2,0	493,5	4,70	475.5	440	125	53,8	5.0	0,32
8	0÷325	2,5	303,5	0,5	384,5	4,75	424,5	255	105	54,4	7,5	0,23
9	0÷355	1,5	336,5	1,5	494,5	6,05	615,5	295	95	53,5	7,5	0,35
10	0÷375	2,5	371,5	2,5	484,5	5,25	515,5	265	125	58,5	7,5	0,37
11	0÷385	1,5	381,5	2,0	443,5	4,25	640,5	275	113	28,5	5,0	0,31
12	0÷265	2,5	247,5	0,5	257,5	5,45	645,5	285	114	37,5	7,5	0,40
13	+135÷-135	1,5	126,5	2,5	387,5	4,15	442,5	325	115	54,7	5,0	0,41
14	+155÷-155	1,5	143,5	1,5	577,5	6,15	594,5	343	165	46.8	7,5	0,34
15	+115÷-115	1,5	105,5	0,5	361,5	7,45	547,5	135	445	48,5	10,0	0.16
16	+125÷-125	2,5	121,5	0,5	366,5	4,65	449,5	175	260	49,5	7,5	0,15
17	+135÷-135	0,5	123,5	2,5	462,5	6,05	615,5	548	140	68,5	10,0	0,19
18	+155÷-155	0,5	128,5	2,0	344,5	5,35	510,5	445	255	61,5	7,5	0,29
19	+145÷-145	2,5	127,5	1,5	344,5	4,35	412,5	375	270	62,8	7,5	0,39
20	+135÷-115	2,5	99,5	0,5	444,5	6,25	619,5	370	175	47,5	10,0	0,42
21	+145÷-145	0,5	138,5	2,5	258,5	5,25	519,5	385	180	49,6	7,5	0,52
22	0÷455	1,5	347,5	0,5	358,5	4,25	419,5	305	195	40,6	5,0	0,61
23	0÷465	2,5	457,5	2,0	458,5	6,75	671,5	355	135	45,8	7,5	0,16
24	0÷475	0,5	438,5	1,5	271,5	5,75	571,5	455	130	44,3	7,5	0,14
25	+225÷ -125	1,5	214,5	2,5	371,5	4,95	491.5	340	125	34,5	7,5	0,12
26	+225÷ -100	2,5	213,5	1,5	471,5	5,95	591.5	395	225	37,5	10,0	0,11
27	+225÷ -220	0,5	215,5	0,5	261,5	6,55	644,5	425	105	38,8	10,0	0.32

ЗАНЯТТЯ №3

«Розрахунок похибок та запис кінцевого результату вимірювання при одноразових прямих вимірюваннях та непрямих опосередкованих вимірюваннях»

1. Мета заняття

Засвоїти визначення похибок і їх вплив на результати вимірювання за одноразових прямих та опоседкованих вимірювань.

2. Завдання на виконання роботи

3.1. Основні загальні положення

При прямому вимірюванні похибка його результату в більшості випадків

визначається класом точності використаного ЗВ, який характеризує його інструментальну похибку.

Інструментальні похибки - це складові похибки вимiрювання фізичної величини, якi залежать від похибки використаних засобів вимiрювання.

Вони визначаються конструктивними, технологічними або схемними недоліками ЗВ.

Інструментальні систематичні похибки виявляють шляхом перевірення засобу вимiрю­вання по зразковому ЗВ більш високої точності.

Методичні похибки - складові похибки вимiрювання, якi виникають через недосконалість методу вимiрювання та граничними межами точності значень використаних фізичних констант і припущень в розрахункових формулах.

Опосередковано вимірювана величина У зв’язана з величинами – аргументами X1, X2,…, Хі,…, Xn деякою функціональною залежністю F, то, в загальному, можна записати:

У = F(X1, X2,…, Хі,…, Xn).

Ця залежність є основою для розрахунку похибок при таких вимірюваннях

Похибка непрямого опоседкованого вимірювання визначається похибками результатів вимірювання кожного виконаного прямого вимірювання.

Тому із урахуванням результатів проведених прямих вимірювань величин-аргументів в певній точці характеристики перетворення, загальний результат Увим опосередкованого вимірювання має вигляд:

Увим = F(Х + ΔХ1, Х +ΔХ2, …, Х +ΔХn), (3.1)

де Х , Х , … , Х – істинні (дійсні) значення аргументів;

ΔХі – абсолютні похибки вимірювань цих аргументів.

Ураховуючи те, що значення похибки вимірювання завжди суттєво менше самої вимірюваної величини, функція F по залежності (3.1) може бути із високою точністю надана, в межах точки із координатами істинних значень аргументів, розкладом у ряд Тейлора, в якому враховані тільки складові першої степені:

У F( , ,…, ) + , (3.2)

де ΔУ – абсолютна похибка загального результату вимірювання;

- перша частинна похідна від функції F по Х -тому аргументу;

- відхилення результату вимірювання і-того аргументу від істинного його значення, тобто, абсолютна похибка вимірювання і-того аргументу.

У реальних умовах ця формула дає дещо завищене значення похибки ΔУ,

так як при додаванні складових похибок можлива їхня часткова взаємна компе-

сація. Кращі результати дає середньоквадратичне підсумовування похибок:

ΔУ , (3.3)

де - часткова похибка результату опосередкованого вимірювання.

Відносна похибка опосередкованого вимірювання:

= = (3.4)

Якщо формула зв’язку є функцією добутку змінних Х та Х з коефіцієнтом К та показниками степені a та b (будь-які цілі або дробові, додатні або від’ємні числа): У = К Х Х , то відносна похибка

= ΔУ / У = , або. (3.5)

ΔУ = У . (3.6)

Якщо в результатах прямих вимірювань аргументів були використані надійні межі загальних похибок, то похибки опосередкованих вимірювань також відображають надійні межі загальних похибок цих результатів.

Кінцевий запис РВ опосередкованого вимірювання:

У = А_У ± Δ_У, (3.8)

А_У - найбільш вірогідне значення вимірюваної величини за формулою зв’язку;

Δ_У - розрахована її похибка вимірювання.

3.2. Приклади розв’язування задач на визначення похибок одноразового опосередкованого вимірювання

В усіх прикладах результати розрахунків показувати (як мінімум) з 5-ма знаками після коми. Округлювати результати за відповідними правилами тільки для запису кінцевого РВ !!!!!!!!!!

Задача №3.1. Визначення похибок одноразового прямого вимірювання.

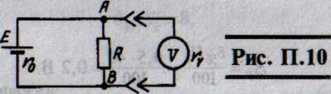Рис.1

Визначити і записати як кінцевий РВ значення абсолютної та відносної методичної систематичної складової похибки вимірювань при вимірюванні спаду напруги на опорі вольтметром V, яка виникає із-за впливу кінцевого значення його опору r_V. У схемі на рис.1: живлення Е = 15,1 В; внутрішній опір джерела живлення r₀ = 2 Ом; опір R = 100 Ом; а опір вольтметра r_V = 12 кОм.