Лекция 1

Определение 1. Матрицей размера mn называется таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются ее элементами.

– символическое обозначение матрицы с элементами .Числа m и n называются размерностями матрицы.

Матрица называется квадратной, если m = n. Число n в этом случае называют порядком квадратной матрицы. Если все элементы кв.м. стоящи вне гл.д. =0-матрица диагональная. Если в диог.м. эл-ты гл.д. =1,то-единичная. Квадратная матрица наз. верхняя треугольная, если все эл-ты столбцов ниже гл.д. =0.Если m не= n то-прямоугольная.

С матрицами связаны следующие операции и понятия:

1. Умножение матрицы на число (скаляр)

Эта операция определена для матриц любого размера (порядка).

2. Сложение (вычитание) матриц

3. Транспонирование матрицы

.

4. Произведение двух матриц.

Линейные операции над мат-ми.

А+В=В+А

(А+В)+С=А+(В+С)

α(βА)=(αβ)А

(α+β)А= αА+βА

α(А+В)= αА+ Αв

Определитель n-го порядка

есть сумма n! членов каждый из которых соответствует одному из n! упорядоченных множеств полученных r попарными перестановками элементов из множества 1,2,…,n.

Замечание 1. Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.

Замечание 2. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.

Лекция 2

Основные свойства определителей.

Сформулируем и докажем основные свойства определителей 2-го и 3-го порядка (доказательство проведем для определителей 3-го порядка).

Свойство 1. Определитель не изменяется при транспонировании, т.е.

Доказательство.

=

Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.

Свойство 2. При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

.

Доказательство.

Свойство 3. Определитель, имеющий нулевую строку, равен 0.

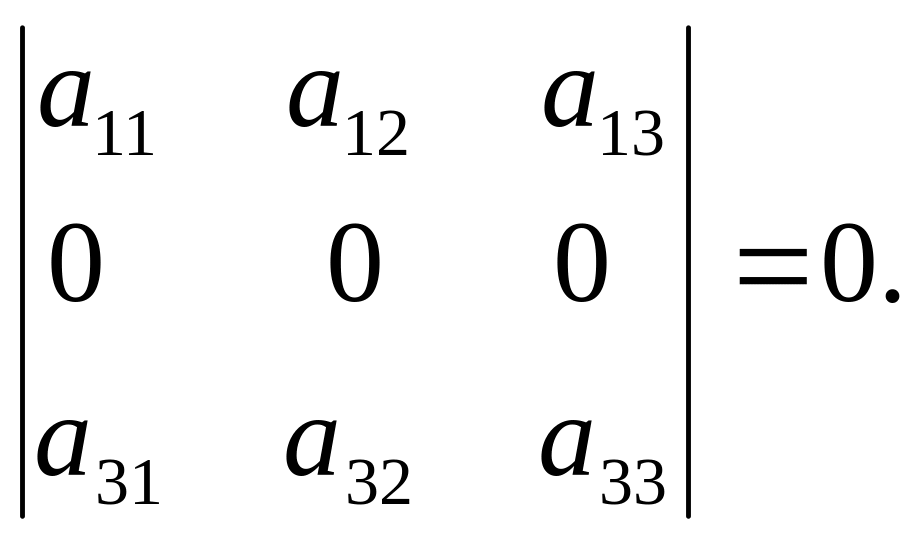
Доказательство этого свойства следует из свойства 2 при k = 0.

Свойство 4. Определитель, имеющий две равные строки, равен 0.

Доказательство.

Свойство 5. Определитель, две строки которого пропорциональны, равен 0.

Доказательство следует из свойств 2 и 4.

Свойство 6. При перестановке двух строк определителя он умножается на –1.

Доказательство.

Свойство 7.

Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5.

Свойство 8. Величина определителя не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Доказательство следует из свойств 7 и 5.

Элементарные преобразования мат-ц.

1.перестановка строк( ) местами.

2.пребавление одной строки( ) к другой.

3.умножение строки на число не=0.

Вычесление опредилителя п-го порядка.

Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.

Определителем квадратной матрицы называется число, получаемое из ее элементов по определенному правилу.

Алгебраическим дополнением элемента матрицы A n-ого порядка называется его минор, взятый со знаком (-1)^i+j :

.

Минором элемента матрицы A n-ого порядка называется определитель матрицы (n-1)-го порядка, полученной из матрицы A вычеркиванием i-ой строки и j-го столбца.

Определителем матрицы первого порядка называется элемент и обозначается .

Определитель матрицы A n-го порядка равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения

(разложение по элементам i–ой строки; i=1,2,…n);

(разложение по элементам j–го столбца; j=1,2,…n)

Метод Гаусса.

Метод Гаусса – метод последовательного исключения неизвестных. Этот метод является универсальным потому, что позволяет решать системы любого числа уравнений с любым числом неизвестных, а если система не имеет решения, то метод позволяет установить это в ходе решения.

Сущность метода в том, что посредством элементарных преобра-зований система приводится к равносильной системе ступенчатого вида, за к-шагов.

Определение 3.8. Квадратная матрица В называется обратной к квадратной матрице А того же порядка, если АВ = ВА = Е. При этом В обозначается .

Рассмотрим условие существования матрицы, обратной к данной, и способ ее вычисления.

Обратная матрица.

Теорема. Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной.

Доказательство.

1. Необходимость: так как то (теорема 3.1), поэтому

2. Достаточность: зададим матрицу в следующем виде:

.

Тогда любой элемент произведения (или ), не лежащий на главной диагонали, равен сумме произведений элементов одной строки (или столбца) матрицы А на алгебраические дополнения к элементам друго столбца и, следовательно, равен 0 (как определитель с двумя равными столбцами). Элементы, стоящие на главной диагонали, равны Таким образом,

= . Теорема доказана.

Замечание. Сформулируем еще раз способ вычисления обратной матрицы: ее элементами являются алгебраические дополнения к элементам транспонированной матрицы А, деленные на ее определитель.

Квадратная матрица А называется вырожденной, если , и невырожденной, если .

Лекция 3

СЛАУ.

Определение. Линейными операциями над какими-либо объектами называются их сложение и умножение на число.

Определение Линейной комбинацией переменных называется результат применения к ним линейных операций, т.е. где числа, переменные.

Определение Линейным уравнением называется уравнение вида

(2.1)

где и b – числа, - неизвестные.

Таким образом, в левой части линейного уравнения стоит линейная комбинация неизвестных, а в правой – число.

Определение. Линейное уравнение называется однородным, если b = 0. В противном случае уравнение называется неоднородным.

Ах=В х=А\В

1.если А=0,В не=0-решений нет.

2.А=0,В=0-бесконечное множество решений.

3.А не=0 х=А\В.

Определение. Системой линейных уравнений (линейной системой) называется система вида

(2.2)

где , - числа, - неизвестные, n – число неизвестных, m – число уравнений.

СЛАУ наз. совместн. если сущ. хотя бы одно решение этой системы, если решений нет-несовместной.

Если СЛАУ имеет 1 решение, то она наз. определенной, если больше, то неопределенной.

Определение Решением линейной системы (2.2) называется набор чисел

которые при подстановке вместо неизвестных обращают каждое уравнение системы в верное равенство.

Правило Крамера.

Рассмотрим систему : Назовем главным определителем этой системы определитель , элементами которого являются коэффициенты при неизвестных:

.

Предположим сначала, что Умножим каждое уравнение системы (2.3) на алгебраические дополнения элементов j-го столбца

Сложив затем все уравнения, получим:

. (2.5)

Отметим, что .

(j-й столбец)

(Результат получен из разложения определителя по j-му столбцу). Такой определитель равен 0 при и равен при i = j. Правая часть равенства (2.5) представляет собой определитель , в котором вместо j-го столбца стоит столбец свободных членов системы (2.3). Назовем такой определитель . Рассматривая j = 1,2,…,n, получим систему, эквивалентную исходной: (2.6) . Разделив все уравнения на , найдем единственное решение: .

Предположим теперь, что =0. Тогда система (2.6) примет вид: .

В этом случае, если все =0, система выглядит так: и имеет бесконечно много решений. Если же хотя бы один из система решений не имеет.

Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:

1. Если система (2.3) имеет единственное решение, определяемое по формулам: .

2. Если = =0, система имеет бесконечно много решений.

3. Если =0, а хотя бы один из система не имеет решений.

Решение невырожденных СЛАУс помощью обратной матрицы.

Рассмотрим линейную систему (2.3): и введем следующие обозначения:

- матрица системы, - столбец неизвестных,

- столбец свободных членов. Тогда систему (2.3) можно записать в виде матричного уравнения: АХ = В. (3.1)

Пусть матрица А – невырожденная, тогда существует обратная к ней матрица

Умножим обе части равенства (3.1) слева на Получим

Но тогда , а поскольку (3.2)

Итак, решением матричного уравнения (3.1) является произведение матрицы, обратной к А, на столбец свободных членов системы (2.3).

Ранг матрицы – это порядок ее наибольшего ненулевого минора. Обозначения: r(A), R(A), Rang A.

Базисным минором матрицы называется любой ее ненулевой минор, порядок которого равен рангу матрицы.

Строки (столбцы) матрицы называются линейно зависимыми, если существует их линейная комбинация, не все коэффициенты в которой равны 0, равная нулевой строке (столбцу).

В противном случае строки (столбцы) называются линейно независимыми.

Теорема о базисном миноре.

Теорема Строки и столбцы матрицы, элементы которых входят в базисный минор, линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией этих строк (столбцов).

Доказательство (для строк).

1. Если бы базисные строки были линейно зависимыми, то с помощью эквивалентных преобразований из них можно было бы получить нулевую строку, что противоречит условию, что базисный минор не равен 0.

2. Строка, входящая в базисный минор, является линейной комбинацией его строк, в которой коэффициент при данной строке равен 1, а остальные коэффициенты равны 0.

Докажем это свойство для строки, не входящей в базисный минор.

Добавим к базисному минору эту строку (пусть ее номер – k) и любой столбец матрицы (пусть его номер – j). Затем разложим полученный определитель, равный 0 (так как его порядок больше ранга матрицы) по j-му столбцу:

Поскольку является базисным минором, поэтому, разделив полученное равенство на , найдем, что

для всех j=1,2,…,n, где . Следовательно, выбранная строка является линейной комбинацией базисных строк. Теорема доказана.

Для нахождения ранга матрици ее приводят к ступенчатому виду( матрица А наз. ступенчатой, если под 1ым эл-том каждой строки стоят 0) с помощью элементарных преобразований(перестановка местами строк( ),умножение на число строку ( ), прибавление к строке ( ) линейной комбинации др. строк( ).

теорема Кронекера-Капелли

Линейная система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Теорема (теорема Кронекера-Капелли). Система

совместна тогда и только тогда, если ранг матрицы системы равен рангу расширенной матрицы.

Доказательство.

1. Необходимость: пусть система совместна и ее решение. Тогда

, (4.1) то есть столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добавление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, то есть

2. Достаточность: если то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации то эти числа будут решением системы т.е. эта система совместна. Теорема доказана.

Условие единственности решения слау.

Если ранг матрицы совместной сист. меньше числа неизвестных( r меньше n), то сист.имеет бесконечное множество решений. Если r = n сист. имеет единственное решение.

Лекция 4

Решение однородных СЛАУ.

, где все b=0- сист. из n ур-й, с m неиз. Ах=0.

Общие св-ва однородных систем: 1. всегда совместна (имеет тривиальное решение х=0; если х-решение однородной сист., то сх-решенее; если х1 и х2- решение, то их линейная комбинация также решение (с1х1 +с2х2)

Пусть в сист. rgА=r меньше n, базисный минор стоит в левом верхнем углу. Из теоремы о базисном миноре следует, что все ур-ия начиная с (r+1) явл. линейными комбинациями первых r уравнений и их можно отбросить. Получаем укороченную сист.

Придавая свободным неизвестным свободные решения и решая (2) по ф-лам Крамера получим не тривиальное (не0) решение сист. Отсюда следуют следующие теоремы:

- если rgA=r≤n, то однородная сист. имеет не тривиальное решение.

- квадратичная однородная сист. имеет нетривиальное решение, если detA=0.

Придадим свободным неизвестным следующие n-r наборов значений: 1) х =1, х =0; 2) х =0, х =1, х =0, х =0; n-r) х =0, х =1

Полученные частные решения запишем в виде вектор-столбцов х1,х2,…,хn-r.

Эти решения наз. нормальной фундаментальной сист. решений.

Справедливы теоремы:

Пусть х1,х2,…,хn-r- нормальной фундаментальной сист. решений, тогда:

- эта сист. линейнонезависима

- произвольное решение х явл. линейной комбинацией ФСР.

Х=с1х1+с2х2+…+сn-rxn-r,где с1,с2,сn-r- const.

Док-во: 1)(линейнонезав-ма.) Составим матрицу из столбцов х1,х2,…,хn-r. В последних n-r строк стоит минор

Отсюда следует, что х1,х2,…,хn-r линейнонезависимы(теорема о базисном миноре)

2) Пусть произвольные решения однородной сист.

с1= хr+1; c2= xr+2;...; cn-r = xn.

y = x-(c1x1+c2x2+...+cn-rxn-r)

Из св-в однородной сист. следует что Ау=0(у - явл. решением однородной сист.) С другой стороны вектор у записывается в виде:

Т.к. все свободные неизвестные – 0, то все базисные неизвестные тоже 0. Отсюда у = 0, т.е. х = с1х1+с2х2+…+сn-r*xn-r.

Определение. ФСР однородной сист. наз. произвольной набор n-r линейнонезависимых решений. Утверждение теоремы справедливо для любой ФСР.

Структура общего решения неоднородной линейной системы.

Пусть дана совместная сист. из m ур-й с n неизвестными Ах = в (1) Соответствующая однородная сист. Ах =0 (2).

Теорема: Общее решение неоднородной сист. (1) есть сумма частного решения этой сист. + общее решение однородной сист. (2).

Док-во: Пусть х4 – частное решение неоднородной сист. Ах4 = в (3); вычитая из(1) (3) получим Ах- Ах4 = 0 или А(х-х4)=0 Отсюда следует, что х-х4 является решением однородной сист.

х-х4=с1х1+…+ сn-r*xn-r, где х1,…,хn-r – ФСР однородной сист.

Из последнего равенства следует: х = х4+(с1х1+…+ сn-r*xn-r)

Лекция 5

Линейное пространство.

ОПР.: Множество L элементов произвольной природы (их обозначают как вектора) называются линейным пространством, если:

- для любых , принадлежит L определена сумма + принадлежащая L

- любое принадлежащее L и любого вещественного числа α определено α принадлежащее L

Примеры линейных пространств.

1) Арифметическое коорд. пр-во Rⁿ. Эл-ты – векторстроки длины n: = (x₁ ,x₂ ,x₃ , … ,x_n ). Операции введены след. образом:

- α = (αx₁ , αx₂ , αx₃ , … , αx_n )

- + = (x₁+y₁ , x₂+y₂ , x₃+y₃ , … , x_т+y_n )

2) Множество векторов трехмерного пространства с обычными операциями сложения, умножения на число

3) Множество прямоуг. матриц размера m×n

4) Множество многочленов степени =< n с одной переменной x.

5) Множество c[a,b] функций непрерывных на отрезке [a,b]

Простейшее свойства линейных пространств

1. + = +

2. ( + )+ = +( + )

3. Существует нулевой эл-т принадлеж. L такой, что + =

4. Для любого сущ. (- ) такой, что +(- ) =

5. 1· =

6. α(β ) = (αβ)

7. (α+β) = α + β

8. α( + ) = α + α

Линейная зависимость и независимость векторов.

ОПР.: Система эл-тов ₁ , ₂ , ₃ , … , _n принадлежащая L называется линейнозависимой, если сущ. числа α₁ ,α₂ ,α₃ , … ,α_n, из которых хотя бы одно отлично от нуля такие, что выполнено неравенство

α ₁ ,α ₂ ,α ₃ , … ,α _n = (1)

Если равенство (1) выполнено лишь при α₁=α₂=α₃ =…=α_n = 0, то система линейно независима.

Лемма.

Система элементов линейно зависима тогда и только тогда, когда один из элементов системы явл. линейн. комбинацией остальных.

Пример

Система линейно зависима

₁ = (1,1,1)

₂ = (2,3,4)

₃ = (4,5,6) т.к. x₃ = 2 ₁+ ₂

Базис и размерность линейного пространства.

ОПР.:

Линейное пространство L наз. n-мерным если в нем сущ. система из n линейно независимых эл-тов, а любые (n+1) эл-ты линейно зависимы. Число n называется размерностью пространства и обозначается dim L

ОПР.:

Базисом n-мерного пространства наз. произвольная система из n линейно независимых векторов.

Базис обычно обозначается

Разложение вектора по базису.

Теорема о разложении по базису.

Пусть – базис пр-ва L , произвольный вектор L можно разложить по базису, т.е. представить в виде x_{1 1}+x_{2 2}+…+x_{n n}= (1)

В разложении (1) числа x₁,x ₂,…,x _n называются координатами в данном базисе.

Если базис фиксирован пишут = ( x₁,x ₂,…,x _n)

Док-во:

Запишем систему из (n+1) эл-тов: , . По определению размерности эта система линейно зависима , т.е. (2)

В равенстве (2) 0, т.к. в противном случаи будут линейно зависимы. Разделив (2) на и обозначив _k= - получим (1)

Координаты в данном базисе.

Действия с координатами.

1. При сложении векторов координаты складываются

2. При умножении вектора на число координаты умножаются на это число

Исследование линейной зависимости и независимости в координатах.

Пусть в n-мерном пр-ве задано m векторов координатами в некотором базисе

………………………

Матрица из системы векторов называется матрица, по строкам которой стоят координаты векторов.

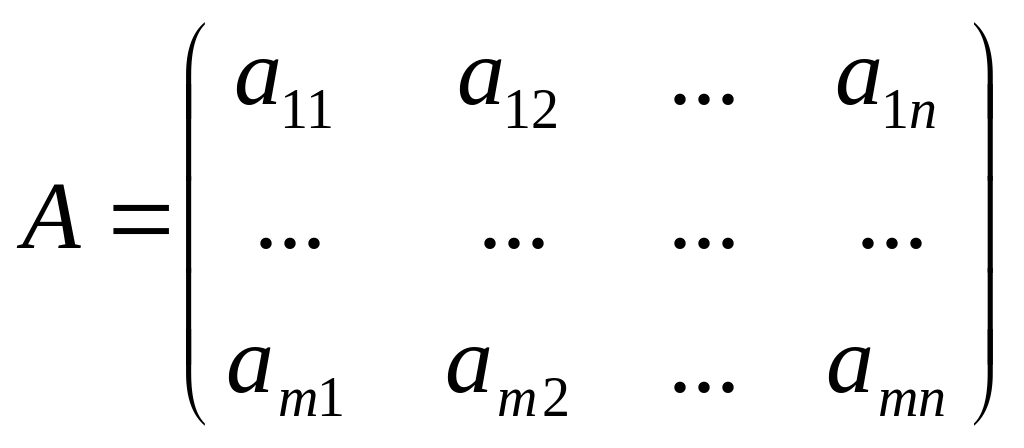
Из теоремы о базисном миноре следует теорема:

Если rg A = r < m, то система линейно зависима.

Если rg A = r = m, то система линейно независима.

Преобразование координат при переходе к новому базису.

Два базиса n-мерного пространства L

Произвольный вектор L можно разложить как по старому так и по новому базисам

Как связаны старые и новые координаты?

Разложим новый базис по старому:

…………………..................

ОПР.:

Матрицей перехода Т от базиса называется матрицей, по столбцам которой стоят координаты новых базисных векторов в старом базисе

Теорема

Пусть и коорд. вектора соответственно в базисах ₁ и ₂ тогда

; (1) (2)

Где Т – матрица перехода от к

В матричной записи последнее равенство эквивалентно формуле (1)

Лекция 6

Подпространства линейного пространства.

Множество L₁ L называется подпространством L если:

1)для любых , L₁ , + L₁

2)для любых L₁ , α L₁

Лемма

Каждое линейное подпространства само явл. линейным пространством.

Примеры:

а) Множество многочленов =< n явл. подпространством множества непрерывных функций c[a,b]

б) В множестве матриц размера n×m подпространство образуют симметричные матрицы, для которых

в) В пространстве Rⁿ подпространство образуют элементы, координаты которых удовлетворяют равенству x₁ + x₂ +…+ x_n = 0

Линейная оболочка векторов.

Самым важным примером подпространства явл. линейная оболочка векторов.

ОПР.: Линейной оболочкой векторов называется множество всех линейных комбинаций этих векторов вида где

Часто обозначают L ( )

Линейная оболочка явл. подпространством.

Справедлива теорема:

Размерность линейной оболочки векторов равна max числу линейнонезависимых векторов в системе.

Пересечение и сумма подпространств L₁ и L₂.

Суммой L₁ + L₂ подпространств L₁ и L₂ называется множество векторов вида ,

где L_1, L_2,

Пересечением L₁ L₂ называется множество векторов, принадлежащих одновременно L₁ и L₂

Прямая сумма.

Сумма L₁ + L₂ называется прямой, если L₁ L₂ = пересечение пустое множество.

Если сумма прямая, то пишут L = L₁ L₂

Если L = L₁ L₂ то произвольный вектор L единственным образом представляется в виде:

, где L_1, L_2,

Теорема о размерности суммы.

Размерной суммой 2-х пространств равна сумме их размерностей минус их пересечения.

dim (L₁ + L₂) = dim L₁ + dim L₂ – dim (L₁ L₂)

графическое пояснение:

площадь фигур равна площади фигур L₁ и L₂ минус их пересечения

L₁ L₂

Лекция 7

Линейные операторы.

Пусть L и R два линейных пространства. Оператором A , действующим из L в R называется правело, которое каждому вектору L ставит в соответствие единственный вектор R

Пишут: =A

Вектор R называется образом , а вектор называется прообразом . Операторы, действующие из L в R называются часто преобразованиями.

А из L₁ в R называются линейными если выполнено условие:

1) A(α ) = Aα

2) A( ₁+ ₂) = A ₁+ A ₂

Из этих св-в следует A(α ₁+β ₂) = Aα ₁+ Aβ ₂

Примеры линейных операторов.

Пусть L = R³

полагают:

1. А = =( ₁, ₂, ₃) – это оператор изменения на число при =0, получим нулевой оператор, при =1 – тождественный оператор E =

2. Оператор проектирования A

3. A

A

Матрица оператора.

Пусть А-линейный оператор из L в - базис в L

Вектора L поэтому их можно разложить по базису:

Матрицей оператора А в базисе называется матрица по столбцам которой :

Связь координат образа и прообраза.

Пусть =A

Найдем связь между координатами x и y

С одной стороны:

=A =A( )= =

С другой стороны:

отсюда получаем:

В матричной записи получаем формулу где А=(а_{i j}) – матрица оператора А

Вывод: координаты образа получаются из столбца координат прообраза умножения на матрицу оператора A

Изменение матрицы при переходе к другому базису.

Пусть А=(а_{i j}) матрица оператора А в базисе , а А^’=(а_{i j})^’ матрица того же оператора в базисе , тогда справедлива формула. А^’=Т^-1 ·А·Т

где Т – матрица перехода от к

Док-во

Пусть =A . Обозначим координаты векторов , в старом базисе : через , и в новом базисе , . На основании формул, связ. координаты образа и прообраза:

(1) где А=(а_{i j})

(2) матрица оператора в старом и в новом базисах

На основание формул преобразование координат при переходе к новому базису

(3) где Т- матрица перехода (4)

Подставляя (3), (4) в (1) получим (5)

Умножая (5) на Т^-1 получим (6)

Из сравнения (2) с (6) следует А^’=Т^-1 ·А·Т

ОПР.: Матрицы А и В называются подобными если существует невыраженная матрица В такая, что В=Т^-1 ·А·Т

Из доказанной формулы следует, что матрица операторов в разных базисах подобна

Св-ва подобных матриц:

1. Их ранги одинаковы

2. Их определители равны

Докажем 2

det В = det|Т^-1 ·А·Т| = det Т^-1· det А ·det Т = det А

Лекция 8