
- •Практическое занятие №4 симплексный метод
- •Цель работы:
- •Содержание работы:
- •Выполнение:
- •Методические указания:
- •Отчет должен содержать:
- •Контрольные вопросы:
- •Задания для практической работы №4 симплексный метод
- •Вариант 1.
- •Вариант 2.
- •Вариант 3.
- •Вариант 4.
- •Вариант 5.
- •Вариант 6.
- •Вариант 7.
- •Вариант 8.
- •Вариант 9.
- •Вариант 10.
- •Вариант 11.
- •Вариант 12.
- •Вариант 13.
- •Вариант 14.
- •Вариант 15.
- •Вариант 16.
Практическое занятие №4 симплексный метод
(2 часа)
Цель работы:
Формирование навыков построения моделей задач ЛП;
Формирование навыков решения задач ЛП симплексным методом без применения инструментальных сред;
Формирование навыков решения задач ЛП симплексным методом в Excel с использованием надстройки Поиск решения;
Формирование навыков решения задач ЛП симплексным методом в MathCAD с использованием функций Minimize и Maximize.
Содержание работы:
Ознакомьтесь с теоретическим материалом;
Выполните задания из пункта 4;
Ответьте на контрольные вопросы.
ПЕРЕЧЕНЬ ОБОРУДОВАНИЯ И ПО:
ПК;
MS Office 2007;
MS Excel 2007с надстройкой Поиск решения;
MathCAD
Выполнение:
Постройте математическую модель задачи линейного программирования. Установите форму полученной записи ЗЛП. Преобразуйте ее к форме основной ЗЛП. Решите ЗЛП симплексным методом без использования инструментальных средств.
Решите ЗЛП симплексным методом в MS Excel, используя надстройку «Поиск решения».
Решите ЗЛП симплексным методом в MathCAD.
Методические указания:
Общей
задачей линейного программирования
называется задача, которая состоит в
определение максимального (или
минимального) значения функции
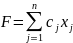 (1) при условиях
(1) при условиях
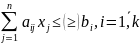 (2)
(2)
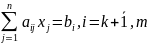 , (3)
, (3)
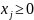 ,
(4)
,
(4)
где
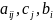 - заданные постоянные величины.
- заданные постоянные величины.
Основной или канонической задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (1) при ограничениях вида (3) и (4).
Решение задачи ЛП симплексным методом включает следующие этапы:
Находят опорный план
Составляют симплекс таблицу
Выясняют, является ли хотя бы одно число дельта, отрицательным
Находят направляющие столбец и строку
Определяю по формулам компоненты нового опорного плана
Проверяют новый план на оптимальность
Если в пакете MS Excel недоступна утилита Поиск решения, то установить ее можно выполнив последовательно: Office > Параметры Excel > Надстройки > Поиск решения > Ок.
Задание 1.
По условию задачи вашего варианта:
1. Составьте и запишите математическую модель задачи.
2. Установите форму записи полученного условия.
3. Если требуется, то внесите изменения в формулировку так, чтобы форма записи соответствовала основной ЗЛП.
4. Запишите условие задачи в векторной форме. Выделите базисные векторы.
5. Составьте и заполните исходную симплекс-таблицу.
6. Вычислите числа дельта и определите по их значениям - является ли найденный опорный план оптимальным.
7. В случае не оптимального опорного плана определите ведущие столбец и стоку, ведущий элемент. Составите новую систему базисных векторов. Вычислите коэффициенты векторов в новом базисе. Занесите все вычисления в таблицу.
8. В случае оптимального опорного плана запишите его и определите значения целевой функции при найденном опорном плане.
Задание 2.
Решите задачу ЛП симплексным методом в MS Excel, используя надстройку Поиск решения.
Замечание: Задача решается на основе изначально полученной формулировки задачи, до ее преобразования в основную форму.
В ячейку А1 введите «Практическая работа №4», в ячейку D1 введите свои фамилию и инициалы, в ячейку F1 введите свою группу.
В ячейку А2 введите номер решаемой задачи, в ячейку А3 введите «Имя», в ячейку А4 введите «Значение», в ячейку С2 введите «Переменные», в ячейку А7 введите «Коэффициенты ЦФ», в ячейку F5 введите «Целевая функция», в ячейку F6 введите «Значение», в ячейку G6 введите «Направление», в ячейки В3-Е3 введите переменные «х1», «х2», «х3» и т.д. (столько, сколько переменных в Вашей задаче). Выделите ярким цветом ячейки В4-Е4 и F7.
В ячейки В7-Е7 введите коэффициенты переменных из целевой функции.
В ячейку С9 введите «Ограничения», в ячейку А10 введите «Вид», в ячейки А11-А13 введите «Ограничение 1», «Ограничение 2», «Ограничение 3» (столько строчек, сколько ограничений в решаемой Вами задаче), в ячейку F10 введите «Левая часть», в ячейку G10 введите «Знак», в ячейку Н10 введите «Правая часть».
В ячейку Н11 введите «max» или «min», в зависимости от заданной задачи. В ячейки В11-Е13 введите коэффициенты при переменных х1-х4 из системы ограничений. В ячейки Н11-Н13 введите свободные коэффициенты из системы ограничений.
В ячейку F7 введите формулу для вычисления значения целевой функции: «=B7*B4+C7*C4+D7* D4+E7*E4» или «=СУММПРОИЗВ(B$4:E$4;B7:E7)».
В ячейки F11-F13 введите формулы «=B11*B4+C11*C4+D11* D4+E11*E4» или «=СУММПРОИЗВ(B$4:E$4;B11:E11)»; «=B12*B4+C12*C4+D12* D4+E12*E4» или «=СУММПРОИЗВ(B$4:E$4;B12:E12)»; «=B13*B4+C13*C4+D13* D4+E13*E4» или «=СУММПРОИЗВ(B$4:E$4;B13:E13)». На экране в указанных ячейках после введения соответствующих формул появятся нули.
Рабочее поле после ввода всех данных и условий задачи выглядит следующим образом:
На вкладке «Данные» нажимаем кнопку «Поиск решения».
Далее в поле «Установить целевую ячейку» вводим «$F$7», вводим направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению», в поле «Изменяя ячейки» вписываем «$B$4:$E$4».
Нажав кнопку «Добавить», вызываем окно «Добавление ограничения». В поле «Ссылка на ячейку» введите адреса ячеек переменных «$B$4:$E$4». В поле знака открываем список предлагаемых знаков и выбираем знак ≥. В поле «Ограничение» вводим ячейки нижней границы значений переменных, то есть «$B$5:$E$5». Затем нажимаем кнопку «Добавить» в окне «Добавление ограничения».
В поле «Ссылка на ячейку» вводим ячейку левой части второго ограничения «$F$11». В соответствии с условием задачи (1.1) выбираем в поле знака необходимый знак. В поле «Ограничение» вводим адрес ячейки правой части рассматриваемого ограничения «$H$11».
Аналогично вводим ограничения $F$12>=$H$12, $F$13<=$H$13.
Окно «Поиск решения» после ввода всех необходимых данных задачи (1.1) выглядит следующим образом:

Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить».
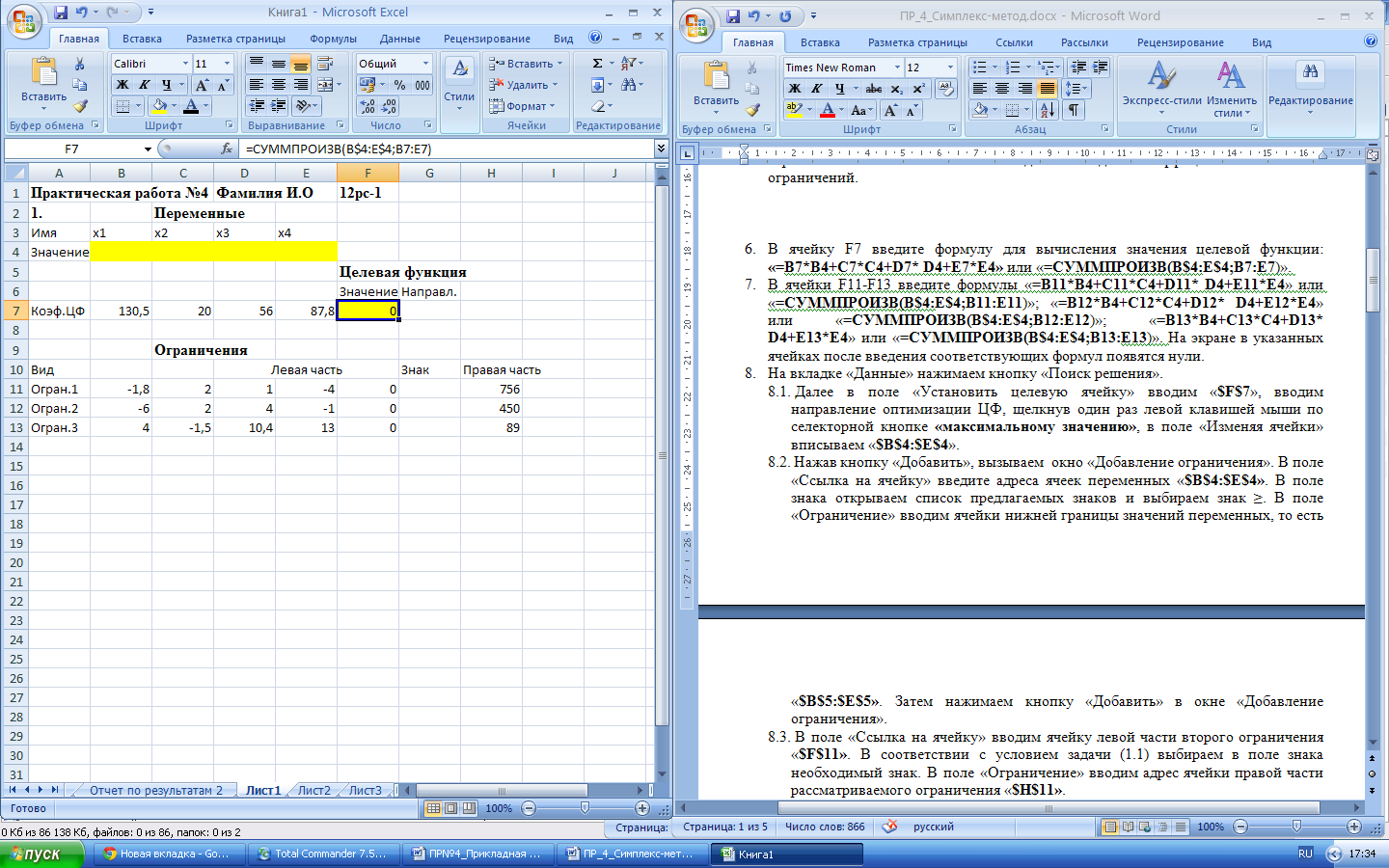
Для установления конкретных параметров решения задач оптимизации определенного класса, необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения». Подтвердите установленные параметры нажатием кнопки «OK».
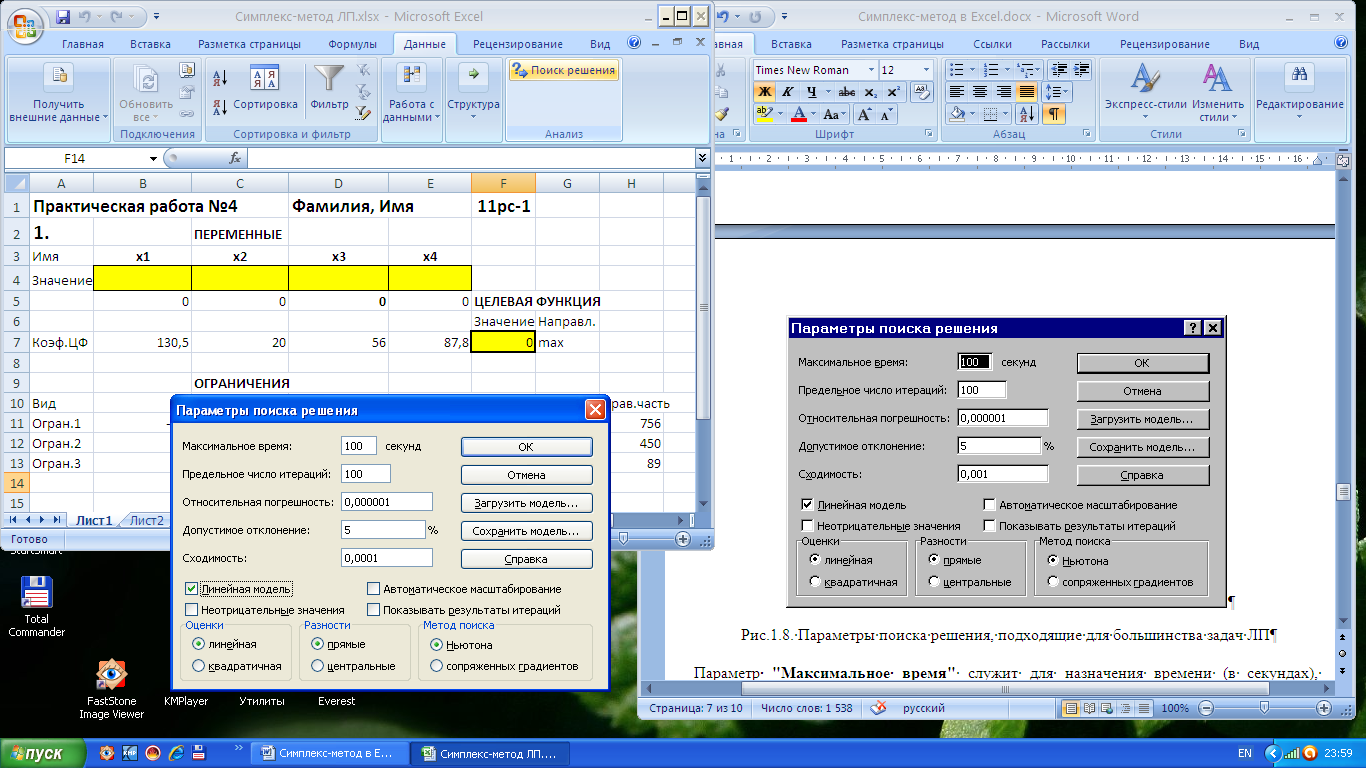
Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить». После запуска на решение задачи ЛП на экране появляется окно «Результаты поиска решения» с одним из сообщений:
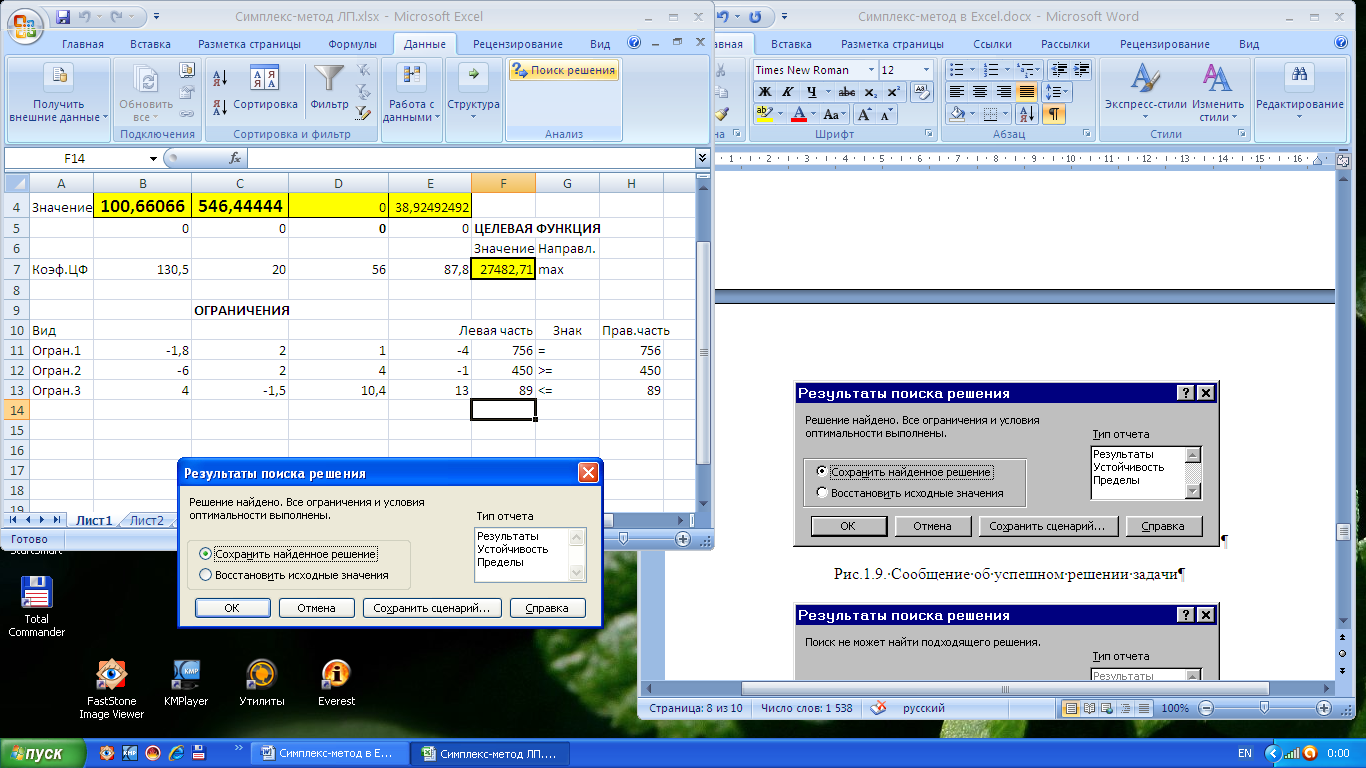
Сообщение об успешном решении задачи
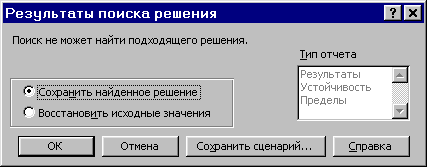
Сообщение при несовместной системе ограничений задачи
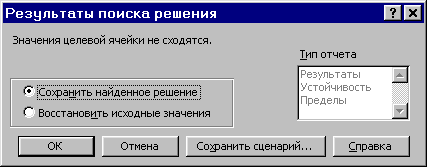
Сообщение при неограниченности ЦФ в требуемом направлении.
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Для получения ответа (значений переменных, ЦФ и левых частей ограничений) щелкните на «Результаты» и нажмите кнопку «OK».
После этого в экранной форме появляется оптимальное решение задачи:
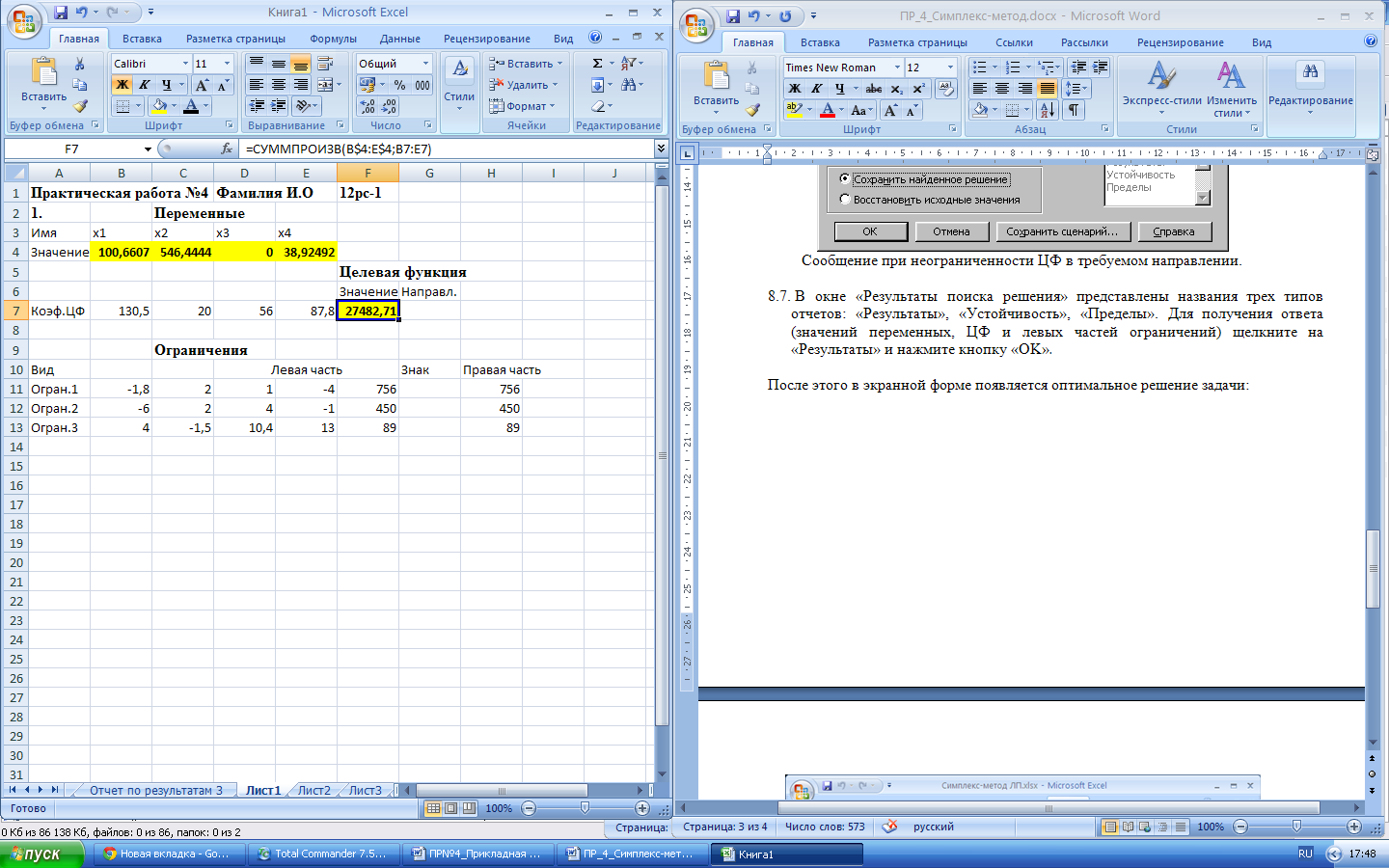
Вывести на печать результат решения задачи, включая Отчет по результатам, который появляется внизу MS Excel.
Задание 3.
Решите задачу ЛП симплексным методом в MathCAD.
1. Откройте в среде MathCAD новый документ и внесите в него математическую модель решаемой вами задачи. Для набора текста на русском языке выберите шрифт Courier New. Для создания текстового блока нажмите «.
2. Для ввода условия задачи используем ее матричное представление. Для создания матриц раскрывается панель «Матрицы», выбирается шаблон и в окне настроек задается число строк и столбцов создаваемой матрицы. Так для целевой функции записываем с:= (для этого знака нажимаем литеру :) и вызываем шаблон матрицы из одного столбца и количества строк равного количеству неизвестных в задаче. Шаблон заполняем данными по условию задачи. Для задания начального значения неизвестных записываем х:= и вызываем шаблон матрицы. Шаблон заполняем нулями. Далее записываем f(x):=c*x.
3. Для задания системы ограничений создаем матрицы а и в. Матрица а - прямоугольная, число строк - число ограничений в задаче, число столбцов - число неизвестных. Заполняется она коэффициентами при неизвестных системы ограничений задачи. Матрица в - такая же как с и х. Заполняется она свободными коэффициентами системы ограничений задачи.
4. Далее (обязательно ниже) записывается служебное слово Given за которым записывается система ограничений, а именно а*x<=b и x>=0
5. Далее вводится новая переменная y. А именно y:=Maximize(f,x) Для поиска минимального значения задается y:=Minimize(f,x)
6. Для получения результата записываем y= и выполняем щелчок ЛКМ в произвольном месте страницы.
7. Для нахождения максимального значения целевой функции записываем f(y)= и и выполняем щелчок ЛКМ в произвольном месте страницы.
