Упражнения
Решить уравнение колебания ограниченной струны:
Ответ:
.
Ответ:
.
Ответ:
Ответ:
.
Ответ:
.
Ответ:
.
Ответ:
.
Глава 3. Уравнение теплопроводности. Решение уравнения теплопроводности методом Фурье
Вывод уравнения теплопроводности
Рассмотрим однородный теплоизолированный с боков стержень конечной длины l имеющий постоянную по длине толщину, и настолько тонкий, чтобы в любой момент времени температуру тела во всех точках поперечного сечения можно было бы считать одинаковой.
Выберем
ось х
(направив ее по оси стержня) так, чтобы
стержень совпадал с отрезком
оси
х.
Обозначим
температуру стержня в сечении х
в момент времени t
через
.
Тогда функция
дает закон распределения температуры
в стержне. Выведем дифференциальное
уравнение для этой функции.
Выделим
элемент стержня
и составим для него уравнение теплового
баланса, согласно которому скорость
изменения количества тепла в
рассматриваемом объеме, обусловленная
теплоёмкосью материала, равна количеству
тепла, поступившему в этот объем в
единицу времени вследствие теплопроводности.
Скорость изменения тепла в выделенном
элементе стержня равна
,
где
– теплоемкость материала стержня,
– плотность материала,
– площадь поперечного сечения. По
теореме о среднем:
.
Теперь найдем количество тепла, поступившее в выделенный элемент стержня за единицу времени. Так как стержень теплоизолирован с боков, то тепло может поступать только через сечения, ограничивающие выделенный элемент стержня. Поэтому искомое количество тепла с учетом формулы Лагранжа равно:
,
где
- коэффициент теплопроводности.
Составим уравнение теплового баланса
.
Разделим
обе части этого уравнения на
(объем
выделенного элемента стержня) и устремим
(тогда
).
Получим
.
Это
уравнение называется уравнением
теплопроводности для однородного
стержня. Величина
называется коэффициентом
температуропроводности.
Метод Фурье для конечного стержня
Уравнение теплопроводности относится к уравнениям параболического типа.
Будем искать решение уравнения теплопроводности с начальными и граничными условиями:
Частные решения данного уравнения будем искать в виде:
где X (x) – функция только переменного x, T (t) – функция только переменного t.
Подставляя предполагаемую форму решения в уравнение, получим:
или, после деления на ,
.
Правая часть полученного равенства является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение
,
где – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций и :
Очевидно, что нас интересуют нетривиальные решения ( ).
Граничные условия дают:
Отсюда следует
.
Таким образом, мы приходим к простейшей задаче: найти те значения параметра , при которых существуют нетривиальные решения задач:
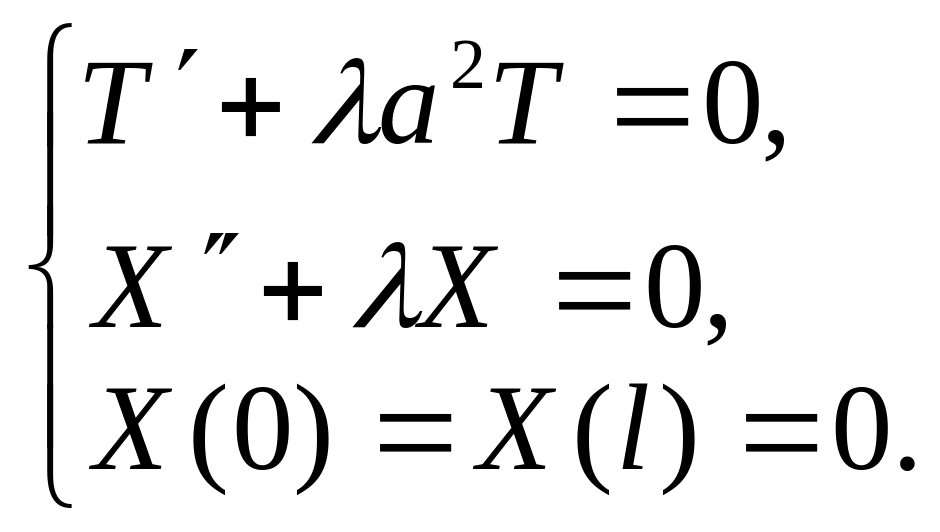
а также найти эти решения.
При
решении уравнения колебания струны
было доказано, что при
и
уравнение
имеет только тривиальные решения,
поэтому рассмотрим только случай
.
Тогда решение уравнения
с учетом граничных условий
имеет вид:
,
а
решение уравнения
имеет вид:
,
где
– неопределенный пока коэффициент.
Тогда частные решения уравнения теплопроводности
,
А общее решение
.
Начальные
условия позволяют определить
:
Для выполнения этого начального условия необходимо взять в качестве коэффициент Фурье:
.
Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.
Пример.
Найти решение
уравнения теплопроводности при граничных
условиях
и начальном условии
Решение. Общее решение уравнения имеет вид:
,
где
.
Вычисляя данный интеграл, получим
, 
.
Получим
.
Так как
,
то
.
Итак,
.