3. Классификация уравнений второго порядка в частных производных

Рассмотрим уравнение второго порядка

, (1)

где .

Обозначим . Тогда уравнение (1) принадлежит

к гиперболическому типу, при ,

к параболическому типу, при ,

к эллиптическому типу, при .

К уравнениям гиперболического типа приводят различные задачи о колебательных процессах. Уравнения параболического типа описывают процессы распространения тепла, диффузии и т.п. К уравнениям эллиптического типа обычно приводят задачи о стационарных тепловых процессах.

Упражнения

13. К какому типу относится уравнение колебания струны ?

Ответ: гиперболическому.

14. К какому типу относится уравнение теплопроводности ?

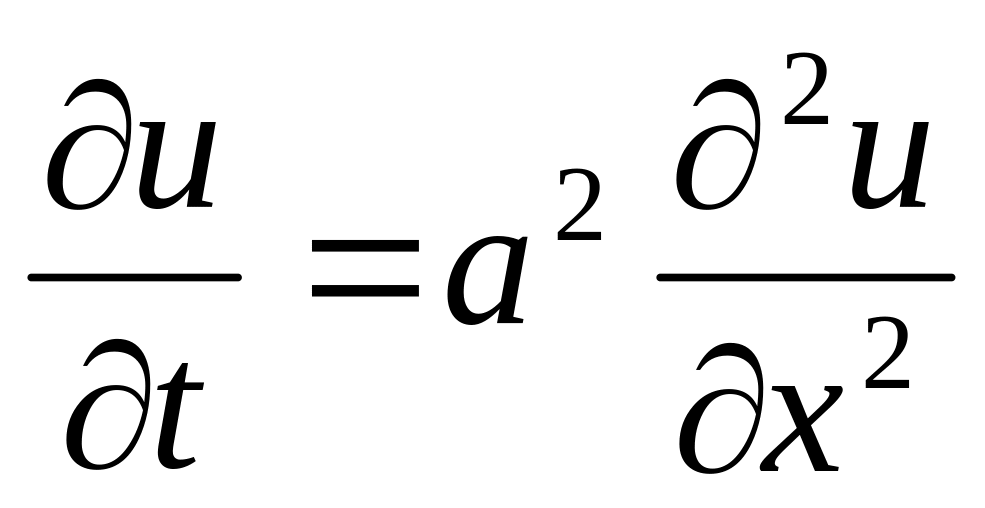Ответ: параболическому.

15. К какому типу относится уравнение Лапласа ?

Ответ: эллиптическому.

Глава 2. Уравнение колебания струны

1. Вывод уравнения колебания струны

Рассмотрим натянутую струну длины l закрепленную на концах. В положении равновесия струна направлена вдоль оси Ox. Сила натяжения T₀, действующая на струну, предполагается значительной. Каждую точку струны длины l можно охарактеризовать значением её абсциссы x и смещением этой точки в момент времени t.

Для упрощения задачи примем следующие предположения:

1.   Будем рассматривать только поперечные колебания струны, предполагая, что движение происходит в одной плоскости, и что все точки струны движутся перпендикулярно оси Ox.

Тогда процесс колебания струны может быть описан одной скалярной функцией , которая характеризует (вертикальное) смещение точки струны с координатой x в момент времени t.

2.   Будем рассматривать струну как гибкую упругую нить:

• Математической выражение понятия гибкости заключается в том, что напряжения, возникающие в струне, всегда направлены по касательной к ее мгновенному профилю (рис.1). Это условие выражает собой то, что струна не сопротивляется изгибу.

• Понятие "нить" означает, что мы пренебрегаем формой поперечного сечения и толщиной (рассматриваем линейную плотность ρ(x)).

Рис. 1. Профиль струны

3. Рассматриваем только малые колебания струны, т.е. будем считать, что смещение , а также столь малы, что квадратами этих величин по сравнению с 1 можно пренебречь, то есть , .

4.   Величина напряжений (силы натяжения) может быть вычислена с помощью закона Гука: сила натяжения, возникающая в струне, пропорциональна её относительному удлинению:

,

где - начальная длина струны, - удлинение струны, таким образом,

,

где k – коэффициент упругости.

Длина произвольного участка струны (рис.2) в любой момент времени выражается формулой:

.

Таким образом, получаем, что при условии малых отклонений длина произвольного участка струны сохраняется. А значит, можно считать, что величина сил натяжения точек струны не изменяется с течением времени, т.е. имеем .

Рис.2. Мгновенный профиль участка струны в момент времени t

Покажем также, что натяжение не зависит и от x. Найдем проекции натяжения на оси x и u (обозначим их T_x и T_u):

,

,

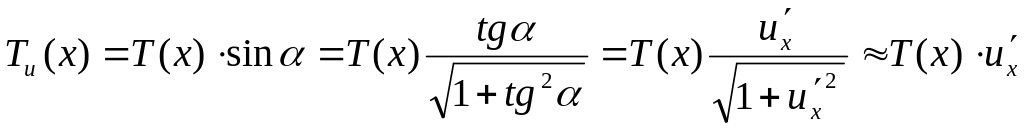где α – угол касательной к кривой) с осью x.

На участок действуют силы натяжения и внешние силы. Сумма проекции всех сил на ось x должна быть равна нулю (мы рассматриваем только поперечные колебания, т.е. струна не движется вдоль оси Ох). Так как внешние силы по предположению направлены вдоль оси u, то

или .

Отсюда в силу произвольности x и следует, что натяжение не зависит от x, т. е. для всех значений x и t:

.

Согласно второму закону Ньютона сумма сил, действующих на участок струны (рис.2) равна по величине и по направлению вектору ускорения этого участка, умноженному на его массу. Определим величины всех сил, действующих на этот участок. Обозначим через плотность распределения внешних сил, вызывающих отклонение точек струны только в вертикальном направлении. Тогда величина внешних сил, действующих на участок , при условии непрерывности функции по переменной х равна:

Далее, силы натяжения и , действующие со стороны левого (в точке ) и правого (в точке ) концов струны, направлены по касательным к мгновенному профилю струны в соответствующих точках.

Для вертикальной составляющей сил натяжения имеем выражение

.

Так как рассматриваем малые колебания, то

Таким образом, сумма сил, действующих на участок струны равна:

(2)

С другой стороны, рассматривая участок струны как совокупность материальных точек, имеем

(3)

где – линейная плотность струны. Приравнивая выражения (2) и (3) и переходя к пределу при , для искомой функции получим уравнение:

или

где .

В том случае, когда на струну не действуют внешние силы, получается уравнение свободных колебаний струны:

или

.

Волновыми эти уравнения называются потому, что они описывают распространение слабых возмущений в упругой среде (т.е. механические колебания с малыми амплитудами), которые в физике называют волнами. Волновые уравнения возникают также в задачах об электрических колебаниях, в гидродинамике и акустике, в теории упругости, при изучении электромагнитных полей.