
- •Глава 1. Дифференциальные уравнения в частных производных. Задача Коши. Типы уравнений второго порядка в частных производных.
- •Дифференциальные уравнения в частных производных.
- •Дифференциальные уравнения в частных производных второго порядка
- •Понятие об общем решении уравнения в частных производных
- •Начальные и граничные условия. Задача Коши
- •Задача Коши для дифференциальных уравнений первого порядка
- •Задача Коши для дифференциальных уравнений второго порядка
- •Классификация уравнений второго порядка в частных производных
- •Глава 2. Уравнение колебания струны
- •Вывод уравнения колебания струны
- •Методы решения уравнения колебания струны
- •Метод Даламбера (метод бегущих волн) для бесконечной струны
- •Фазовая плоскость
- •Метод продолжений для полубесконечной струны
- •Метод продолжения для конечной струны (начальная и конечная точки жёстко закреплены)
- •Метод Фурье (метод стоячих волн). Метод разделения переменных
- •Упражнения
- •Глава 3. Уравнение теплопроводности. Решение уравнения теплопроводности методом Фурье
- •Вывод уравнения теплопроводности
- •Метод Фурье для конечного стержня
- •Упражнения:
- •Приложения Практикум в среде matlab
- •Задача Коши для полуограниченной струны. Метод продолжений.
- •Создание анимации средствами matlab.
- •Фазовая плоскость. Бегущие волны.
- •Индивидуальные задания
Глава 1. Дифференциальные уравнения в частных производных. Задача Коши. Типы уравнений второго порядка в частных производных.
Дифференциальные уравнения в частных производных.
Рассмотрим функцию нескольких
независимых переменных
![]() .
.
Частные производные 1-го
порядка данной функции
по переменной
![]() вычисляются по обычным правилам и
формулам дифференцирования, при этом
все переменные, кроме
,
рассматриваются как постоянные.
вычисляются по обычным правилам и
формулам дифференцирования, при этом
все переменные, кроме
,
рассматриваются как постоянные.
Обозначение:
![]() .
.
Частными производными 2–ого порядка функции называются частные производные от ее частных производных первого порядка.
Обозначение:
![]() .
.
Пример.
Найти частные производные 1-го и 2-го
порядков функции
![]() .
.
Решение:
Считая y
постоянной, получим: ![]() .
Считая x
постоянной, получим:
.
Считая x
постоянной, получим:
![]() .
Соответственно:
.
Соответственно: ![]() ,
,
![]() ,
,
![]() .
.
Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то уравнение называется обыкновенным. Если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.
Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:
 – обыкновенное дифференциальное
уравнение 1-го порядка;
– обыкновенное дифференциальное
уравнение 1-го порядка; – обыкновенное дифференциальное
уравнение 2-го порядка;
– обыкновенное дифференциальное
уравнение 2-го порядка; – обыкновенное дифференциальное
уравнение 3-го порядка;
– обыкновенное дифференциальное
уравнение 3-го порядка;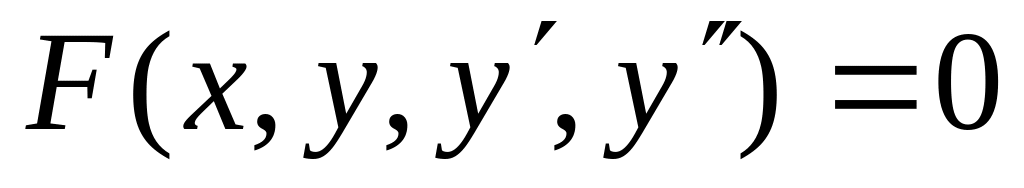 – общий вид обыкновенного дифференциального
уравнения 2-го порядка;
– общий вид обыкновенного дифференциального
уравнения 2-го порядка; – уравнение в частных производных 1-го
порядка;
– уравнение в частных производных 1-го
порядка;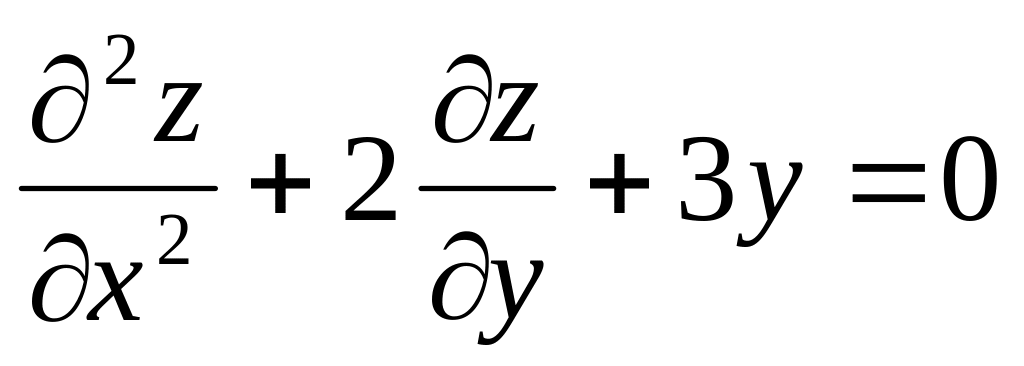 – уравнение в частных производных 2-го
порядка.
– уравнение в частных производных 2-го
порядка.
Решением дифференциального уравнения называется такая дифференцируемая функция, которая при подстановке в уравнение обращает его в тождество.
Дифференциальные уравнения в частных производных второго порядка
Многие задачи механики и физики приводят к исследованию дифференциальных уравнений с частными производными второго порядка. Так, например:
1) при изучении различных видов волн − упругих, звуковых, электромагнитных, а также других колебательных явлений мы приходим к волновому уравнению
![]() ,
,
где а − скорость распространения волн в данной среде;
2) процессы распространения тепла в однородном изотропном теле, так же как и явления диффузии, описываются уравнением теплопроводности:
![]() ,
,
3) при рассмотрении установившегося теплового состояния в однородном изотропном теле мы приходим к уравнению Пуассона
![]() .
.
При отсутствии источников тепла внутри тела уравнение данное переходит в уравнение Лапласа
![]() .
.
Потенциалы поля тяготения и стационарного электрического поля также удовлетворяют уравнению Лапласа, в котором отсутствуют массы и, соответственно, электрические заряды.
Приведенные уравнения называют основными уравнениями математической физики. Их подробное изучение дает возможность построить теорию широкого круга физических явлений и решить ряд физических и технических задач.
Функция
![]() ,
удовлетворяющая какому-либо из приведенных
уравнений, называется его решением.
,
удовлетворяющая какому-либо из приведенных
уравнений, называется его решением.
Понятие об общем решении уравнения в частных производных
Рассмотрим обыкновенное
дифференциальное уравнение n-го
порядка:
![]() .
Его общий интеграл представляет собой
некоторое семейство функций, зависящее
от n произвольных
постоянных
.
Его общий интеграл представляет собой
некоторое семейство функций, зависящее
от n произвольных
постоянных
![]() .
Любое частное решение получается из
него, если параметрам
.
Любое частное решение получается из
него, если параметрам
![]() придать определенные значения.
придать определенные значения.
Рассмотрим решения некоторых дифференциальных уравнений в частных производных.
Пример 1.
Пусть дано уравнение
![]() ,
где
,
где
![]() .
.
Решение: найдем его общий
интеграл, т.е. функцию
![]() ,
удовлетворяющую
данному уравнению. Для этого сначала
запишем это уравнение в виде:
,
удовлетворяющую
данному уравнению. Для этого сначала
запишем это уравнение в виде:
![]() .
Поскольку производная
по переменной х
от величины, стоящей в скобках, равна
нулю, то последняя является некоторой
произвольной функцией от у:
.
Поскольку производная
по переменной х
от величины, стоящей в скобках, равна
нулю, то последняя является некоторой
произвольной функцией от у:
![]() .
Поэтому
.
Поэтому
![]() .
Но интегрируя произвольную функцию
.
Но интегрируя произвольную функцию
![]() ,
получим новую, также
произвольную функцию, скажем
,
получим новую, также
произвольную функцию, скажем
![]() ,
плюс произвольная функция
,
плюс произвольная функция
![]() (
играет роль произвольной постоянной
интегрирования в теории обыкновенных
дифференциальных уравнений). Таким
образом, общий интеграл уравнения
второго порядка
(
играет роль произвольной постоянной
интегрирования в теории обыкновенных
дифференциальных уравнений). Таким
образом, общий интеграл уравнения
второго порядка
![]() содержит две произвольные функции.
содержит две произвольные функции.
Пример 2.
Решить уравнение
![]() ,
где
,
где
![]() .
.
Решение: проинтегрируем обе части уравнения по х:
![]() ,
,
где – произвольная функция.
Пример 3.
Решить уравнение
![]() ,
где
.
,
где
.
Решение: проинтегрируем обе части уравнения по у:
![]() .
.
Получаем
![]() ,
где
–
произвольная функция. Интегрируем
повторно по у
полученное равенство:
,
где
–
произвольная функция. Интегрируем
повторно по у
полученное равенство:
![]() ,
,
где
![]() –
произвольные функции.
–
произвольные функции.
Пример 4.
Решить уравнение
![]() ,
где
.
,
где
.
Решение: проинтегрируем обе части уравнения сначала по х, а затем по у:
![]() ,
,
тогда
![]() ,
,
где – произвольные функции.
Замечание: в отличие от общего решения обыкновенного дифференциального уравнения, зависящего от произвольных постоянных, общее решение уравнения с частными производными зависит от произвольных функций, количество которых равно порядку уравнения.
Упражнения
Найти общее решение следующих дифференциальных уравнений с частными производными. Выполнить проверку.
 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
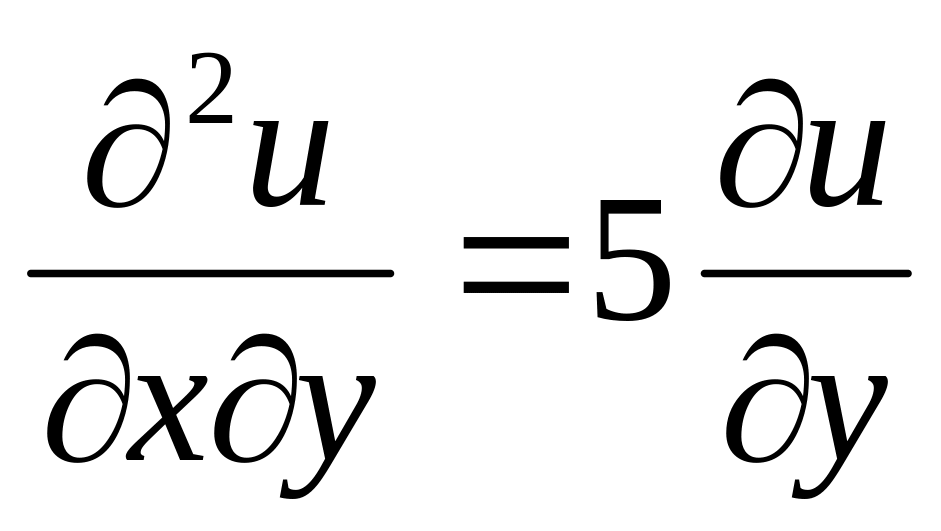 .
.
Ответ:
![]() .
.
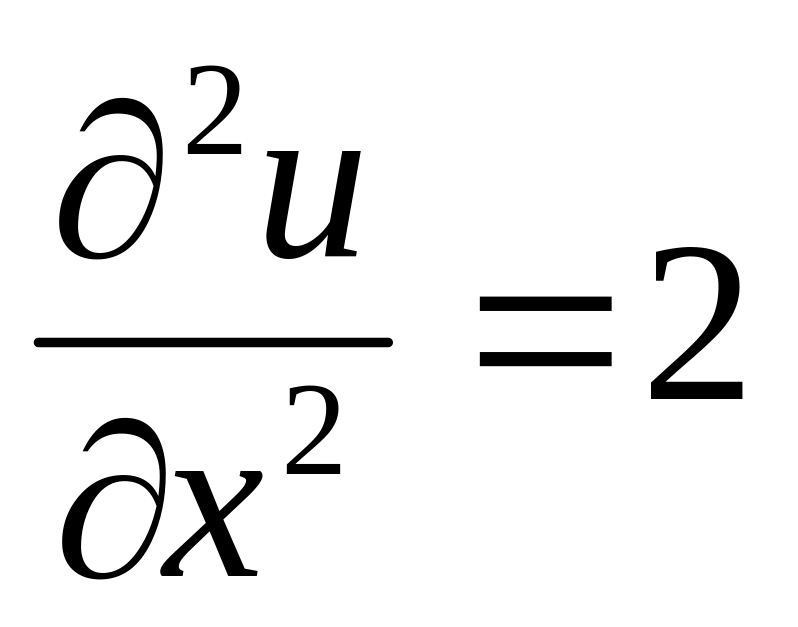 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
 .
.
Ответ:
![]() .
.
Ответ:
![]() .
.
