Справочный материал
Соотношение между тригонометрическими функциями
одного аргумента.
Правило применения формул приведения.
Знак правой части определяется знаком левой части, считая
Если приводимая функция имеет аргумент
то название приводимой функции
сохраняется.Если приводимая функция имеет аргумент
то название приводимой функции меняется
синус на косинус, тангенс на котангенс
и обратно.
Формулы приведения
Для синусa
Для косинуса
Для тангенса и котангенса
.
Формулы сложения
Формулы двойного угла
Формулы половинного аргумента
Формулы преобразования суммы в произведение
Формулы преобразования произведения в сумму
Обратные тригонометрические функции
=b,
b
,
b
[0;
]
,
b
,
b
(0;
)
Имеет место равенство:
,
,
или по таблице значений,
или по таблице значений.
Решение простейших тригонометрических уравнений
Уравнение cos t = a.
Если, |а|>1, то уравнение соs t = а не имеет решений.
Если, |а|1, то,
t = ± агссоs а + 2n, п .
Частные случаи:
cos t = 1, t =2n, n
cos t = -1, t = + 2n, n
cos t = 0, t = + n, n.
Уравнение sin t = a.
Если,
|а|>1, то уравнение
не
имеет решений.
Если, |а|1, то,
Частные случаи:
Уравнение tg t = a, ctg t = a.
Формула корней уравнения tg t = a:
.
Формула корней уравнения ctg t = a:
Тригонометрические неравенства
Неравенства вида Sin t < a |
|
0<a<1 |
-1<a<0 |
t t2 = - П - arcSin a
t2 < t < t1
-П- arcSin a<t<arcSin a |
t t2 = - П + arcSin a
t2 < t < t1
-П+arcSin a<t<-arcSin a |
Учитывая, что arcSin(-|a|) = - arcSin |a| и периодичность функции получаем для любого |a|≤1 решение: -П-arcSin a + 2Пn < t < arcSin a + 2Пn, nZ. |
|
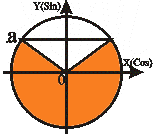
Неравенства вида Sin t ≥ a |
|
t t2 = П - arcSin a
t1 ≤ t ≤ t2 |
t t2 = П + arcSin a
t1 ≤ t ≤ t2 |
Аналогично объединяем два решения: arcSin a + 2Пn ≤ t ≤ П - arcSin a +2Пn, nZ. |
|
1
= arcSin a
1
= - arcSin a
1
= arcSin a
1
= - arcSin aНеравенства вида Cos t ≤ a |
|
0<a<1 |
-1<a<0 |
t t2 = 2П - arcCos a
t1 ≤ t ≤ t2
arcCosa≤t≤2П-arcCosa |
t t2 = П + arcCos a
t1 ≤ t ≤ t2
П-arcCosa≤t≤П+arcCosa |
Учитывая, что arcCos(-|a|) = П - arcCos |a| и периодичность функции получаем для любого |a|≤1 решение: arcCos a + 2Пn ≤ t ≤ 2П - arcCos a + 2Пn, nZ. |
|
Неравенства вида Cos t > a |
|
t t2 = - arcCos a
t2 < t < t1 |
t t2 = - П + arcCos a
t2 < t < t1 |
Аналогично объединяем два решения: - arcCos a + 2Пn < t < П - arcCos a +2Пn, nZ. |
|
1
= arcCos a
1
= П
- arcCos a
1
= arcCos a
1
= П
- arcCos aНеравенства вида tg t < a |
|
0<a<1 |
-1<a<0 |
t t2 = - П/2
t2 < t < t1
-П/2 < t < arctg a |
t t2 = - П/2
t2 < t < t1
-П/2 < t < -arctg a |
Учитывая, что arctg(-|a|) = - arctg |a| и периодичность функции получаем решение: -П/2 + Пn < t < arctg a + Пn, nZ. |
|
Неравенства вида tg t ≥ a |
|
t t2 = П/2
t1 ≤ t < t2 |
t t2 = П/2
t1 ≤ t < t2 |
Аналогично объединяем два решения: arctg a + Пn ≤ t < П/2 +Пn, nZ. |
|
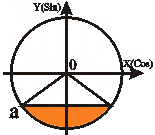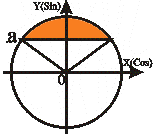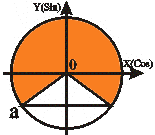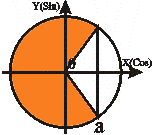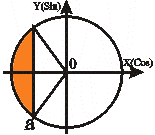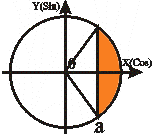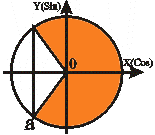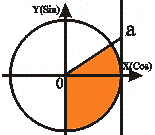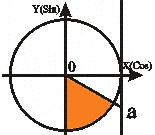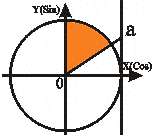1
= arctg a
1
= - arctg a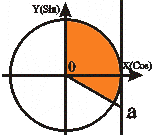
1
= arctg a
1
= - arctg a