Сложные зубчатые механизмы
Одноступенчатые передача, состоящие из двух сопряженных зубчатых колес не позволяют осуществлять большое передаточное отношение. Оно может колебаться от 3 до 7. С точки зрения уменьшения габаритов, повышения долговечности и улучшения условий непринудительной смазки , делать в одной паре колес передаточное отношение больше 6-8 нецелесообразно.
В таких случаях используют сложные зубчатые механизмы, состоящие из нескольких параллельно или последовательно соединенных друг с другом зубчатых колес.
Различают два таких механизма: сложные зубчатые механизмы с неподвижными осями (многократные зубчатые передачи) и планетарные (эпициклические механизмы) оси отдельных зубчатых колес в которых могут перемещаться относительно стойки.
ТЕОРЕМА О ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ ЗУБЧАТЫХ МЕХАНИЗМОВ.
Общее передаточное число любого сложного зубчатого механизма, включающего несколько последовательно соединенных друг с другом простых механизмов (не планетарных ступеней, планетарных или их комбинаций) равно произведению передаточных отношений простых механизмов ( ступеней).
Рассмотрим несколько последовательно соединенных ступеней зубчатых механизмов . Их число q-1.
Докажем, что общее передаточное отношение то есть от звена 1 к звену q равно произведению передаточных отношений ступеней.
u1q=u12*u23*u34*u45…uq-1q
По определению передаточного отношения
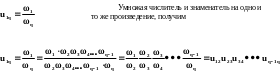
Что и требовалось доказать
СЛОЖНЫЕ ЗУБЧАТЫЕ МЕХАНИЗМЫ
Последовательные ряды зубчатых колес
Последовательный, паразитный ряд это такой ряд в котором выполнено соединение зубчатых колес, при котором каждое ведомое колесо одновременно является ведущим по отношению к следующему, т.е. каждое промежуточное колесо ряда одновременно входит в два зацепления.
1
2
3
4
z2
z1
z4
z3
1
2
3
4
n1
n2
n3
n4
А
В
С
z1
z2
z3
z4
Есть четыре способа показать направления вращения зубчатых колес
Если задано вращение первого колеса ряда (круглая стрелка), то можно расставить стрелки вращения других колес и звеньев по правилу что внешнее зацепление меняет направление вращения, внутреннее нет.
Вращение можно показать и на другой проекции прямыми стрелками, обозначающими скорость движения точек на периферии зубчатых колес. Точки первой пары входят внутрь, у второй пары выходят, у следующей пары снова входят.
Третий способ показать вращение это перечеркивание стрелкой валов. Стрелка показывает направление скоростей видимых наружных волокон.
Четвертый способ показа направления вращения на второй проекции с помощью векторов оборотов или угловых скоростей.
На первой проекции схемы показана также картина скоростей различных точек зубчатых колес. Построение картины скоростей начинается с построения скорости точки А. Скорость точек одинаковы. Изменение скоростей по радиусу линейно. Скорости точек также одинаковы. Аналогично в точке С. Разный наклон эпюр скоростей соответствует разному направлению вращения валов или колес. Тангенсы углов наклона эпюр пропорциональны угловым скоростям.
Это плоский механизм . Для него по определению передаточное отношение имеет знак.
В общем случае передаточное отношение последовательного ряда можно выразить как
Где n -номер колеса последнего в ряду
k - число внешних зацеплений
Если сформулировать словами то передаточное отношение паразитного ряда равно отношению числа зубьев последнего колеса к первому и знак будет определяться числом внешних зацеплений.
Эта формула показывает, что не величину передаточного отношения в таком ряду промежуточные зубчатые колеса влияния не оказывают. Они называются поэтому паразитными. Но на направление вращения они влияют.
Такие ряды применяются : а) для передачи движения между удаленными валами и в) в реверсивных механизмах.
Ступенчатые ряды зубчатых механизмов.
Ступенчатым рядом называется такой, когда ведомый вал предыдущего зубчатого механизма становится ведущим валом последующего механизма.
1
2
3
4
z2
z1
1
2
3
4
А
В
С
z3
z4
z5
z6
z1
z2
z3
z4
z5
z6
VA
VB
VC
+
На рис. Изображен трехступенчатый ряд. В первой ступени движение передается от вала 1 к валу 2 посредством зубчатых колес Z1 u Z2. Во второй ступени передача движения от звена 2 к звену 3 (валам) осуществляется парой колес Z3 u Z4. В третей ступени передача движения от звена 3 к звену 4 (валам) осуществляется парой колес Z5 u Z6.
О
бщее
передаточное отношение есть произведение
передаточных отношений ступеней.
Записывая каждое передаточное отношение
через числа зубьев получим:
Как видим, в определении передаточного отношения участвуют числа зубьев всех колес.
Такие механизмы имеют широкое применение. Например, редуктор механизма поворота крана МКГ-25 использует редуктор, составленный из трех ступеней и открытую передачу.
Общее передаточное число редуктора 11(6,3 3,3 5,9) . Открытая передача имеет передаточное число 14.3 . Общее передаточное отношение 1590.
Последовательно , в виде ступенчатого ряда можно соединять любые трехзвенные зубчатые механизмы.
Решим задачу : соединить последовательно 1 цилиндрическую зубчатую передачу внешнего зацепления; 2 цилиндрическую передачу внутреннего зацепления ; 3 червячную передачу; 4 коническую передачу; 5 цилиндрическую передачу внешнего зацепления.
Общее передаточное отношение равно
