5.4. Расчет деревянных ферм

Расчетные нагрузки, действующие на ферму, состоят из постоянных и временных. Постоянная нагрузка g включает в себя нагрузку от собственного веса всех элементов покрытия и собственного веса фермы, который может быть определен по эмпирической формуле. При этом должны быть учтены коэффи­циенты надежности у и шаг расстановки ферм В. Постоянная нагрузка считается равномерно распределенной по длине проле­та фермы. Временная снеговая нагрузка s определяется по СНиПу и является равномерно распределенной по длине про­лета или по длинам полупролетов фермы. На сегментную ферму может действовать также треугольная снеговая нагрузка Si с максимальными значениями над опорами и нулевым значением в половине пролета фермы (см. расчет сегментных арок).

Ветровая нагрузка w при расчете большинства ферм не учи­тывается, так как она действует в виде отсоса и уменьшает усилия в стержнях ферм от основных нагрузок. При наличии подвесного потолка, чердачного перекрытия или подвесного обо­рудования нагрузки от них сосредоточиваются в узлах нижнего пояса фермы.

Геометрический расчет заключается в определении длин осей всех стержней фермы и углов их наклона к горизон­тальной проекции и между собой в узлах. В сегментной ферме необходимо определить радиус и длину верхнего пояса, длины хорд его стержней, их горизонтальные проекции и стрелы выгиба. При этом можно использовать геометрический расчет сегмент­ной арки.

Статический расчет заключается в определении уси­лий, действующих в стержнях фермы от всех расчетных нагру­зок и их сочетаний. Продольные силы N определяются во всех стержнях фермы. Для этого распределенные нагрузки, действую­щие в верхнем поясе, условно считают сосредоточенными в его узлах. Гнутые оси стержней верхнего пояса сегментной фермы условно заменяют их хордами. Затем определяют продольные силы методами построения диаграммы усилий Максвелла — Кре­мона, вырезания узлов или методом сечений. Примеры построе­ния диаграммы усилий показаны на рис. 8.6.

Продольные силы в стержнях симметричных ферм можно определять только в одной, например, левой половине фермы в следующем порядке. Сначала определяют усилия от равномерно распределенной снеговой нагрузки на одном, например, левом полупролете фермы, затем на одном правом полупролете. Это можно сделать при помощи построения одной диаграммы от левосторонней нагрузки. Усилия от правосторонней нагрузки будут равны усилиям в стержнях незагруженной половины фермы

Рис. 8.6. Нагрузки и усилия в стержнях ферм: ^s а — треугольной; б—сегментной; / — схемы и нагрузки; // — диаграммы усилий Максвелла — Кремона

Продольные силы от равномерно распределенной снеговой нагрузки на всем пролете фермы определяют как сумму сил от нагрузок на полупролетах. Продольные силы от собственного веса определяют путем умножения сил от снеговой нагрузки на всем пролете на отношение значений постоянной нагрузки к снеговой — g/s. Продольные силы можно определять только от треугольной снеговой нагрузки с наибольшим значением на опо­ре, расположенной на левом или правом полупролете фермы.

В верхних поясах всех ферм действуют только сжимающие силы N_c, в нижних поясах — только растягивающие силы N_p, в нисходящих раскосах треугольных ферм — только сжимающие силы N_c и в стойках решетки — только растягивающие силы N_p. В решетке сегментных и многоугольных ферм могут возни­кать как сжимающие, так и растягивающие силы при односто­ронних снеговых нагрузках. Полученные величины продольных сил от отдельных нагрузок и их сочетаний записываются в таб­лицу, форма которой приведена в примере 8,1.

Изгибающие моменты возникают только в сечениях верхних поясов при наличии на них межузловой нагрузки. Их определяют следующим способом. Стержни верхнего пояса рас­сматривают как элементы, шарнирно опертые в узлах, на кото­рые действует межузловая, например равномерно распределенная нагрузка и продольные сжимающие силы, определенные ранее. Силы N действуют вдоль расчетных осей прямых стержней или вдоль хорд гнутых стержней верхнего пояса (рис. 8.7). При равномерно распределенной нагрузке q эти изгибающие моменты

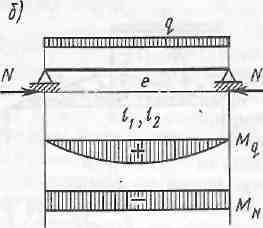
а)

Рис. 8.7. Расчетные схемы работы верхних поясов клеедеревянных ферм:

а — гнутого пояса сегментной фермы; б — прямого пояса треугольной и пяти­угольной фермы

в прямых М_пр и гнутых М_гн стержнях определяют по формулам М_пр = ql²/% - Ne, М_гн = ql²/8 - Nf,

где / — горизонтальная проекция прямого стержня или хорды гнутого; е = (h — ho)/2 — эксцентриситет продольных сил в пря­мом стержне с высотой сечения /г и в концах его /г₀; / = /²/8г) — стрела выгиба гнутого стержня.

В верхнем поясе сегментной фермы максимальный изгибаю­щий момент возникает в опорных стержнях верхнего пояса при треугольной снеговой нагрузке с максимальным значением на опоре фермы. Максимальные поперечные силы Q возникают там же.

Подбор сечений стержней производится с учетом пре­дельно допускаемых их гибкостей X: для стержней верхнего поя­са— 120, для сжатых стержней решетки—150, для стальных стержней нижнего пояса — 400. Расчетные длины поясов в плос­кости фермы принимают равными расстояниям между их узлами. Расчетные длины поясов из плоскости фермы принимают рав­ными расстояниям между закрепленными их связями или между креплениями настилов или прогонов покрытия.

Ширина сечений стержней клеедеревянных ферм принимает­ся, как правило, не больше 17 см, для того чтобы их можно было склеивать из цельных досок без поперечных стыков.

Сечение верхних поясов клеедеревянных ферм подбирают с учетом того, что в них действуют изгибающие моменты М и про­дольные силы N.

Высота сечения верхнего пояса может определяться предва­рительно, приближенно с учетом только продольных сил или только изгибающих моментов по следующим выражениям:

Л_тр = 0,7 N/R_c; h_T, = A/b-₁_ W_Tp = Af/0,8 #„; Ы_Р = ^j6W/b

Проверка напряжении в сечении верхнего пояса производит­ся при сжатии с изгибом по формулам расчета цельнодеревян-ных элементов. При этом определяют его расчетную длину /_р, площадь сечения А, момент сопротивления W и радиус инерции i сечения, гибкость стержня А, коэффициент его устойчивости ф, коэффициент учета деформации |, изгибающий момент с учетом деформаций М_л и максимальное напряжение сжатия о, которое не должно превышать расчетного сопротивления древесины сжатию Re, определяемого с учетом ширины сечения b и коэф­фициентов условий работы — высоты сечения т_в и толщины сло­ев досок, из которых склеен стержень.

Сечения деревянных стержней верхнего пояса и решетки, в которых действуют только сжимающие продольные силы, под­бирают с учетом того, чтобы их ширина была одинаковой, их гибкость не превышала допускаемой. Их рассчитывают на сжа­тие с учетом устойчивости по формулам расчета цельнодере-вянных элементов. Сечения растянутых деревянных стержней подбирают и рассчитывают по формуле расчета цельнодеревян-ных элементов. Сечения растянутых стальных элементов подби­рают и рассчитывают по нормам проектирования стальных кон­струкций. При этом ширина нижнего пояса из стальных уголков должна быть, как правило, равна ширине сечений стержней решетки для удобства решений узлов.

Расчет узлов деревянных ферм. Лобовые упоры узлов деревянных ферм на смятие при действии продольных сжимающих сил вдоль, поперек или под углом к волокнам древесины -определяют! по формулам расчета на смятие цельно-деревянных элементов.

Расчет узлов деревянных ферм обычно производится на действие максимальных усилий соединяемых в них стержней с учетом углов между их осями. Лобовые упоры деревянных эле­ментов в узлах рассчитывают на смятие с учетом того, действуют ли продольные сжимающие силы вдоль, поперек или под углом к волокнам древесины. Число болтов, соединяющих элементы в узлах, определяют с учетом того, работают они вдоль или поперек волокон древесины. Стальные элементы узловых крепле­ний и их сварные соединения рассчитывают по нормам проекти­рования металлических конструкций.

В лобовых врубках проверяют напряжение смятия древеси­ны с под углом к волокнам древесины нижнего бруса под дей­ствием сжимающей силы торца верхнего бруса и напряжение скалывания древесины конца нижнего бруса под действием скалывающей силы Т, равной силе растяжения N нижнего бруса. Этот расчет производится по формуле т= Т/А ^ R_CKXp, где пло­щадь скалывания А = Ы_СК; R_CK._cp = R_CK/{\ + 0,25/_ск/?); e = h/2.

Кроме этого, проверяется напряжение растяжения в ослаб­ленном врубкой сечении нижнего бруса. Расчет ферм по второму предельному состоянию (по про­гибам нижнего пояса) в большинстве случаев, когда фермы имеют рекомендуемые высоты, не требуется. При отношении вы­соты к пролету не менее '/7 фермы имеют вполне достаточную жесткость. Однако в процессе эксплуатации, в основном в ре­зультате податливости их узлов, фермы могут получить не­большие, но заметные на глаз прогибы нижнего пояса. Для исключения таких прогибов нижним поясам ферм рекомендуется придавать дак называемый строительный подъем, равный 1/200 их пролета. Этот подъем учитывается при геометрическом расче­те фермы. При статическом расчете его учитывать не обязатель­но, поскольку он незначительно влияет, на усилия в стержнях фермы.

Расчет по прогибам ферм пониженной против рекомендуемой относительной высоты ' /₇ должен производиться с учетом деформаций всех стержней от действия в них усилий от норма­тивных нагрузок.

Связевые фермы обеспечивают устойчивость основных несу­щих конструкций каркаса, их элементов и воспринимают гори­зонтальные нагрузки, действующие на здание. Они бывают по­перечными и продольными, скатными, вертикальными и наклон­ными.

Скатные поперечные связи (рис. 8.8) являются основными. Они состоят из связевых ферм, которые соединяют верхние пояса или зоны основных несущих конструкций покрытия по­парно. Эти связи располагаются наклонно поперек покрытия в плоскости. Опорами их служат конструкции каркаса стен. Пояса­ми связей служат верхние пояса⁽\ основных конструкций, стой­ками — горизонтальные брусья или прогоны и плиты настила. Решетка бывает перекрестная или раскосная и выполняется из брусьев или стальных тяжей.

а) ^б) 4 р р р р

Рис. 8.8. Связевые фермы: о — профиль связей; б — план связей; в — схема работы связей