Алгебраїчні способи розв’язування систем рівнянь.
1). Спосіб підстановки.
Полягає в тому, що з одного з рівнянь визначають одну змінну через іншу і отриманий вираз для цієї змінної підставляють в друге рівняння, внаслідок чого отримують рівняння з однією змінною. Розв’язавши це рівняння, отримане значення змінної підставляють у вираз для іншої змінної. Отриману пару чисел записують у строгому порядку .
.
2). Спосіб алгебраїчного додавання.
Полягає в тому, що знаходять НСК коефіцієнтів при одній змінній та додаткові множники до кожного з рівнянь, помноживши на які в отриманих рівняннях коефіцієнти при вибраній змінній будуть однакові за модулем і рівні НСК коефіцієнтів при цій змінній у даних рівняннях. Виконавши по членне додавання або віднімання цих рівнянь дістанемо рівняння з однією змінною. Розв’язавши його, отримане значення підставляють в одне з даних рівнянь і дістають рівняння з однією змінною відносно другої змінної. Розв’язавши його. Записують розв’язок системи у вигляді пари .
3). Спосіб порівнювання невідомих.
Полягає в тому, що з кожного з рівнянь виражають одну й ту саму змінну через іншу змінну. Після цього вирази прирівнюють і дістають рівняння з однією змінною. Розв’язують отримане рівняння і знайдене значення підставляють у вираз для іншої змінної. Записують розв’язок у вигляді пари .
4). Спосіб введення нових змінних.
Замість виразів, у які входять змінні x та y вводять нові змінні для спрощення рівнянь системи. Розв’язавши систему відносно нових змінних, повертаються до попередніх змінних.
Іноді, для розв’язування систем рівнянь доводиться комбінувати різні способи.
Приклад.
Розв’язати систему рівнянь різними
способами:
.
1). Спосіб підстановки:
2). Спосіб додавання:
.
.
3). Спосіб порівнювання невідомих:
.
Геометрично множину розв’язків системи рівнянь з двома змінними можна знайти так: будуємо графіки рівнянь
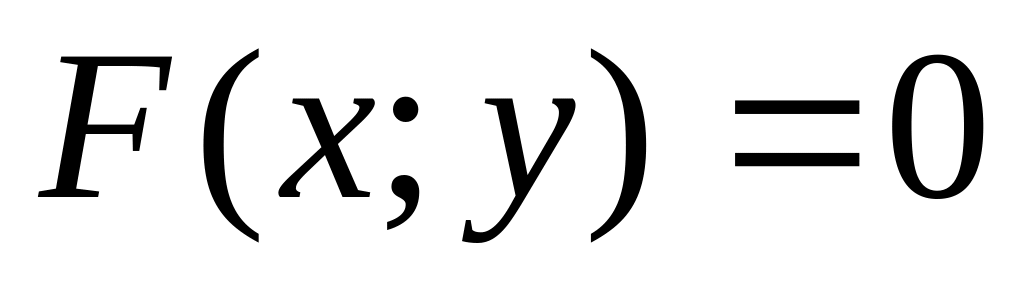і
.
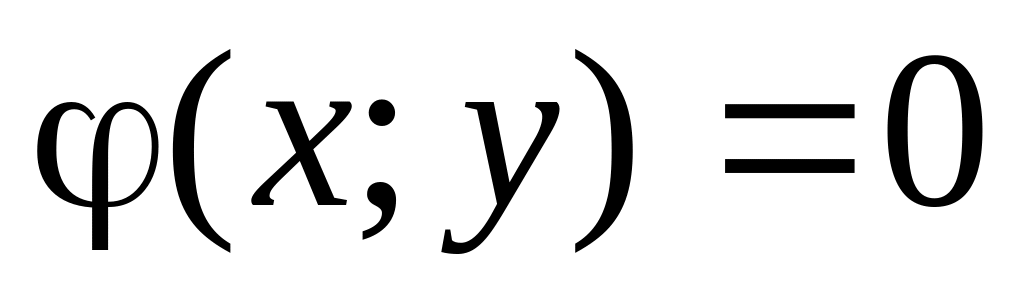Оскільки множина розв’язків системних
рівнянь є перетином множин розв’язків
кожного з рівнянь системи, то знаходимо
точки перетину цих графіків. Якщо такі
точки існують, то координати кожної з
них є розв’язком системи рівнянь. Якщо
таких точок не існує, то система рівнянь
розв’язків не має, тобто множина її
розв’язків є Ø.
Описаний спосіб розв’язування системи
рівнянь називається графічним.
Наприклад. Розв’язати графічно систему рівнянь: .
1).
.
При
:
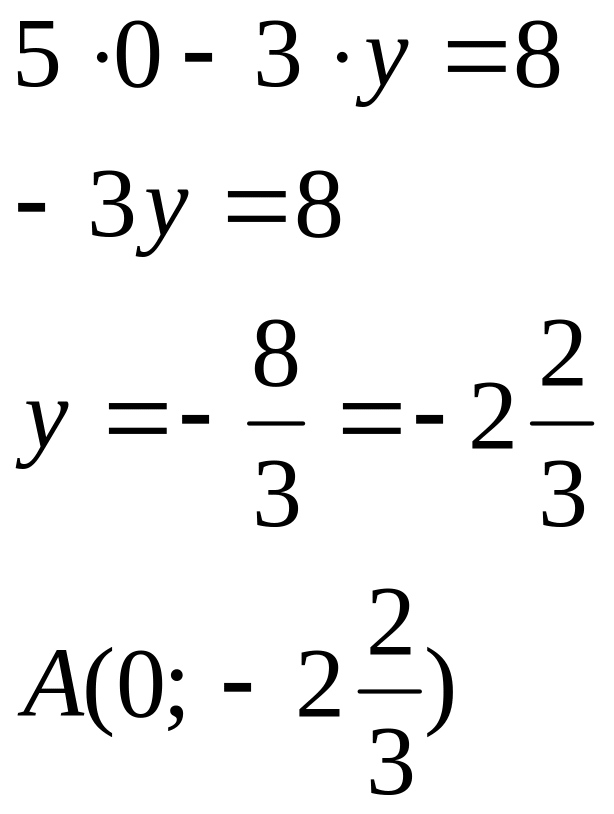
2). При
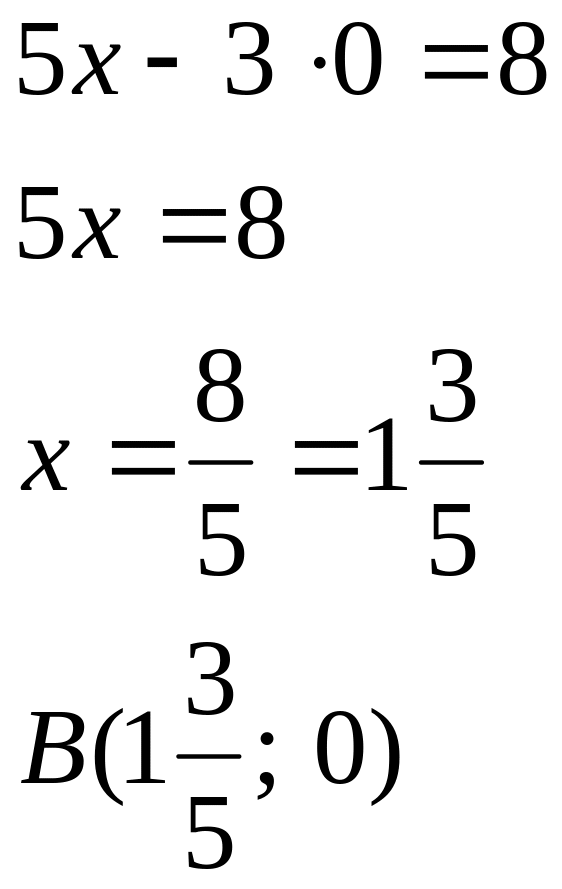
3).
При:
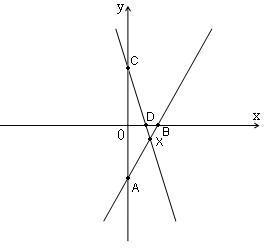
Точка
- єдиний розв’язок.
Відповідь :
Тема 6: Нерівності з двома змінними
План
1. Нерівності з двома змінними, їх системи та сукупності.
2. Графічний спосіб розвязування нерівності систем, та сукупностей нерівностей з двома змінними.
« 1 »
Означення 1 Нерівністю з двома змінними називається двомісний предикат виду
f(x,y) < g(x,y); f(x,y) > g(x,y), де х та у довільні змінні, що набувають числових значень з множини Х.
Означення 2 Пара чисел (х,у) називається розв’язком нерівностей з двома змінними, якщо при підстановці у нерівність одержимо істину числову нерівність.
Кожній нерівності відповідає певна множина розв’язків. Множина розв’язків нерівності, зображена на координатній площині, дає деяку її підмножину. Її називають графіком нерівностей. Будують графік нерівності, використовують геометричний спосіб опису.
Означення 3 Дві нерівності, що мають однакові множини розв’язків, або однакові графіки, називаються рівносильними.
Теореми про рівносильність нерівностей з однією зміною та їх наслідки переносяться на нерівності з двома змінними.
Означення 4 Системою нерівностей з двома змінними називається кон’юнкція двох предикатів. f1 (x,y) > g1 (x,y) ٨ f2 (x,y) > g2 (x,y) і позначається
f1
(x,y)
> g1
(x,y)
f2 (x,y) > g2 (x,y)
Означення 5 Сукупністю нерівностей з двома змінними називається диз’юнкція двох предикатів. f1 (x,y) > g1 (x,y) ٧ f2 (x,y) > g2 (x,y) і позначається
f1
(x,y)
> g1
(x,y)
f2 (x,y) > g2 (x,y)
Означення 6 Розв’язком системи (сукупностей) нерівностей з двома змінними називається пара чисел (х,у) є х2, яка задовольняє кожну (хоча б одну) нерівність системи (сукупностей).
« 2 »
У математиці справедливі такі твердження:
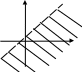
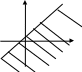
1. Графіком нерівності у<кх+в (у≤кх+в) є нижня півплощина (включаючи пряму у=кх+в) серед півплощин, на які пряма у=кх+в розбиває площину.
у
у
у≤кх+в
у<кх+в
х х
2. Графіком нерівності у>кх+в (у≥кх+в) є верхня півплощина (включаючи пряму у=кх+в) серед півплощин, на які пряма у=кх+в розбиває площину.
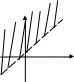
у у
у>кх+в у<кх+в
х х
3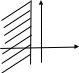
.
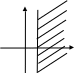Графіком нерівності
х>а
(х<а) є права (ліва) півплощина серед
півплощин, на які пряма х=а розбиває
площину.
у
у
х≥а х≤а
х х
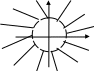
4. Графіком нерівності (х-а)2+(у-в)2<R2((х-а)2+(у-в)2>R2), в якій R>0, є внутрішність (зовнішність) кола з центром т.С (а,в) і радіусом R.
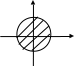
у
у
(х-а)2+(у-в)2 ≤R2 (х-а)2+(у-в)2>R2
х х
Приклад 1
Побудувати графік нерівності:
х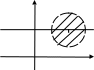
2+у2<8х+6у-21;
у
х2+у2-8х-6у+21<0;
(х2-8х+16)+( у2-6у+9)<-21+16+9; 3
(х-4)2+(у-3)2<4
4 х
П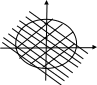
риклад
2
у
Розв’язати графічно систему нерівностей:
х
2+у2-4у-21<0;
4
4х+5у-20<0; 2
х 2+у2-4у+4-25<0; х
5у<20-4х;
х 2+(у-2)2<25;
у<4-0.8х;
Елементи геометрії