Алгоритм розв’язування систем нерівностей

1. Встановити, чи область визначення обох нерівностей однакова.

2. Знайти множини розв’язків кожної з нерівностей і .

3. Знайти множину

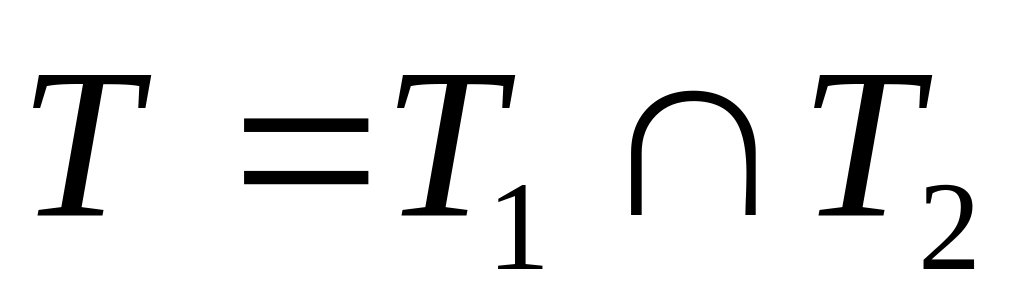
Приклад.

Відповідь: .

Означення 7. Диз’юнкція нерівностей називається сукупність нерівностей з однією змінною і позначається .

Розв’язати сукупність нерівностей означає знайти множину тих значень змінної х з множини Х, при яких хоча б одна з нерівностей перетворювалася в істинну числову нерівність. Множина розв’язків сукупності нерівностей є об’єднання множин розв’язків обох нерівностей.

Алгоритм розв’язування сукупності нерівностей.

1.Встановити чи область визначення обох нерівностей однакова.

2. Знайти множини розв’язків кожної з нерівностей і .

3. Знайти множину

До систем і сукупностей нерівностей приводять окремі види нерівностей:

1. .

З означення

Отже, отримаємо подвійну нерівність або систему нерівностей:

2.

Отримаємо сукупність нерівностей:

3. Дробово – раціональні нерівності:

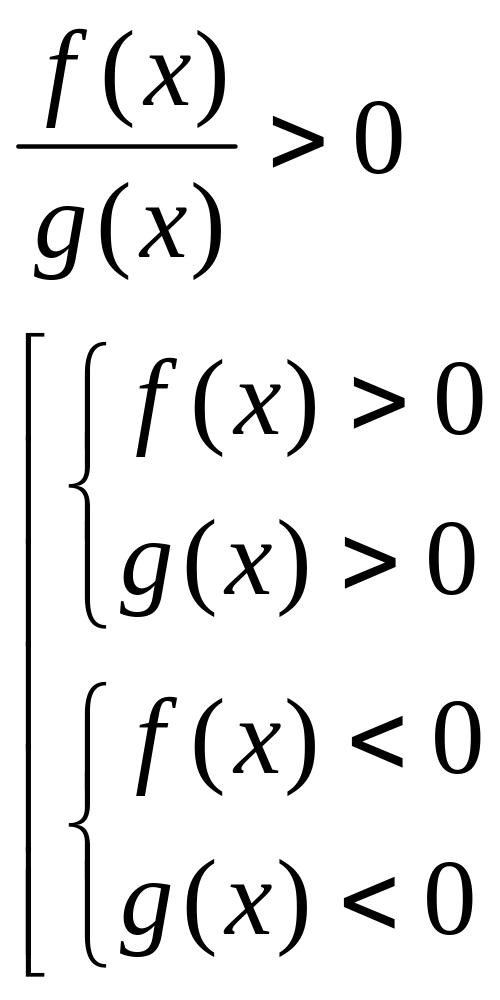
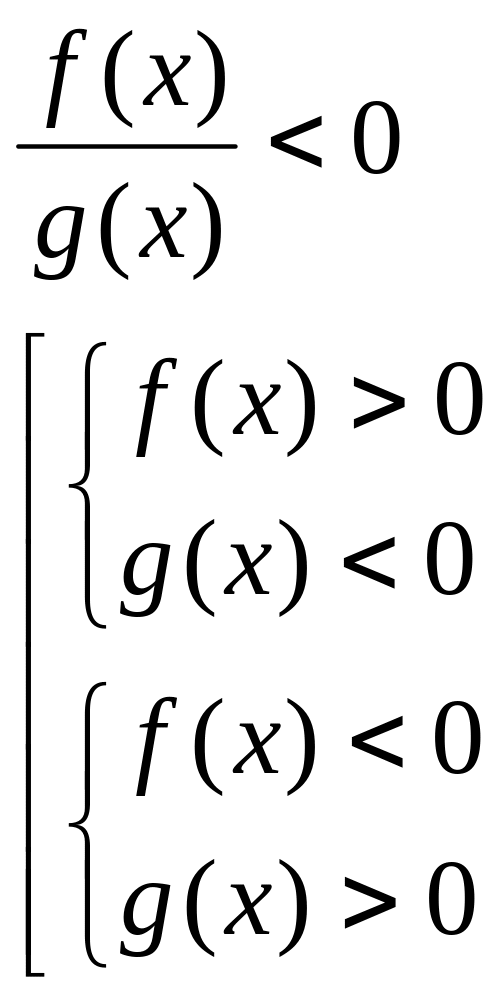
Кожна із нерівностей замінюється сукупністю двох систем при цьому враховуються правила ділення чисел з однаковими ірраціональними знаками.

Тема 5 Рівняння з двома змінними

1. Рівняння з двома змінними.

2. Рівняння лінії та кола.

3. Системи рівнянь з двома змінними. Алгебраїчні способи розв’язування систем рівнянь з двома змінними.

4. Графічний спосіб розв’язування систем рівнянь з двома змінними.

1. Означення 1. Рівняння з двома змінними називається двомісний предикат виду де та довільні змінні, що можуть приймати певні числові значення з множини .

Наприклад:

Множина називається областю визначення предиката . Найчастіше областю визначення є множина . Якщо не вказано область визначення необхідно її встановити, з’ясувавши при яких значеннях змінних та вирази, які входять у рівняння мають зміст.

Будь-яка пара чисел , при підстановці якої у рівняння одержуємо істинну числову рівність називається розв’язком цього рівняння , а множину всіх таких пар – множиною розв’язків рівняння.

Рівняння з двома змінними може мати один розв’язок, кілька, жодного, або нескінченну кількість.

Приклад. 1) , має 4 розв’язки.

2) Т=Ø

3) - один розв’язок.

4) - безліч.

Якщо розглядається одне рівняння з двома змінними, то для того, щоб знайти його розв’язок необхідно:

1. Одній змінній надати довільного значення.

2. Підставити це значення у дане рівняння внаслідок чого отримаємо рівняння з однією змінною.

3. Розв’язати отримане рівняння відносно другої змінної.

4. Записати пару чисел та які є розв’язком рівняння.

Якщо розв’язки рівняння з двома змінними зобразити точками на координатній площині, то ми одержимо на площині деяку множину точок,тобто певну лінію.

Означення 2. Графіком рівняння з двома змінними називається підмножиною точок координатної підмножини, координати яких є розв’язками даного рівняння.

Оскільки рівняння з двома змінними як правило має безліч розв’язків, то графік рівняння з двома змінними містить безліч точок і для його зображення користуються геометричним способом опису.

Означення 3. Два рівняння з двома змінними називаються рівносильними, якщо множини їх розв’язків співпадають.

Теореми про рівносильність рівнянь з однією змінною та наслідки з них переносяться на рівняння з двома змінними.

2. Означення 4. Рівнянням множини точок називаються такі алгебраїчні умови, яким задовольняють координати всіх точок даної множини і не задовольняють координати точок, що не належать цій множині.

Серед геометричних фігур важливе місце займають лінії, наприклад пряма, коло, парабола, гіпербола.

Означення 5. Рівнянням лінії називають рівнянням виду або таке, що виконуються такі умови:

1. Координати будь-якої точки 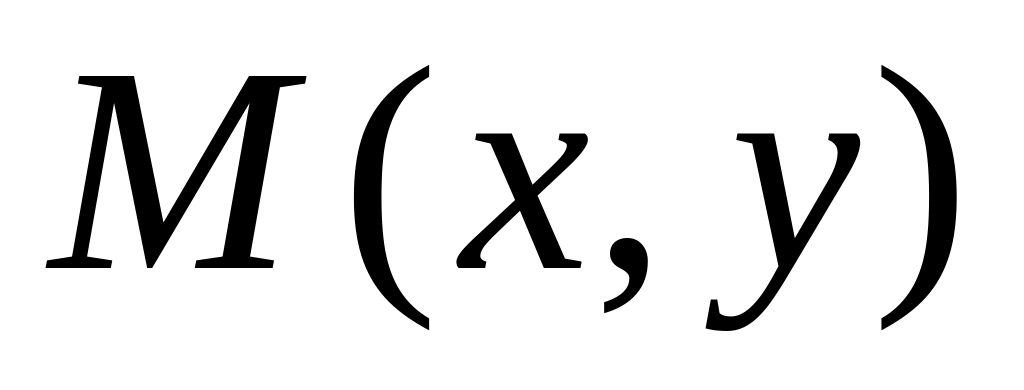, яка належить лінії , задовольняють це рівняння.

2. Будь-яка пара чисел , яка задовольняє рівняння , визначає точку, яка належить лінії :

Будь-яку лінію на площині можна задати:

а) геометричною властивістю;

б) рівнянням.

Розглянемо задачу: Скласти рівняння кола з центром у точці і радіусом R.

Означення 6. Колом називається множина точок площини рівновіддалених від однієї точки, яка називається центром кола.

Р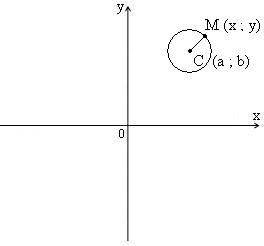 адіус кола – це відрізок, який сполучає центр кола і будь-яку точку кола. Радіус величина стала і задана.

Розглянемо коло в системі координат. т. - центр кола. т. - довільна бігуча точка кола, тоді . Довжина відрізка знаходиться за формулою відстані між двома точками площини .

Отже, - канонічне рівняння кола з центром в т. і радіусом R.

За цим рівнянням можна безпосередньо назвати координати центра кола і радіус. Якщо центр кола співпадає з початком координат, то і рівняння має вигляд .

Розкриємо у рівнянні дужки. Отримаємо: . Позначимо:

- загальне рівняння кола

Будь-яке загальне рівняння кола можна звести до канонічного виду. Це потрібно зробити, щоб визначити центр кола і радіус. Для цього потрібно виділити повні квадрати.

Приклад. Звести загальне рівняння кола до канонічного вигляду: .

Центр кола т. .

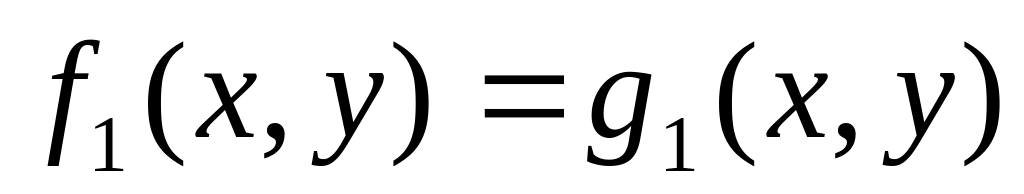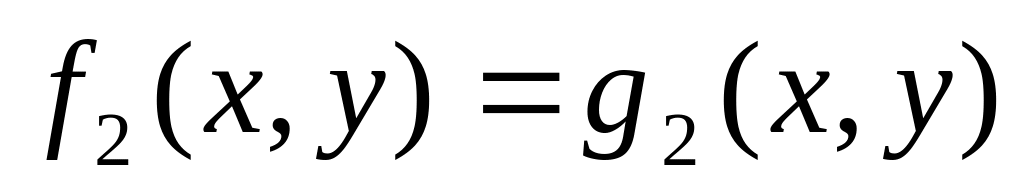3. Нехай дано два рівняння з двома змінними і , які задані на одній і тій самій області визначення. Говорять, що вони утворюють систему, якщо потрібно знайти всі пари чисел, при підстановці яких в кожне рівняння системи, ми отримаємо істинні числові рівності.

В загальному вигляді система записується так:

або

Якщо кожне рівняння розглядати як двомірний предикат, то система рівнянь – це кон’юнкція двох предикатів, для якої необхідно знайти область істинності

Розв’язком системи рівнянь називається пара чисел при підстановці яких в кожне рівняння системи ми одержимо правильні числові рівності. Множина всіх таких пар називається множиною розв’язків даної системи. Множина розв’язків системи є перетином множин розв’язків обох рівнянь системи.

Означення 7. Дві системи рівнянь називаються рівносильними, якщо всі розв’язки однієї системи рівнянь є розв’язками другої і навпаки.

Існують алгебраїчні та геометричні способи розв’язування системи рівнянь.