Тема 3 Рівняння, їх системи та сукупності

1. Рівняння з однією змінною.

2. Рівносильні рівняння.

3. Теореми про рівносильні рівняння та наслідки з них.

4. Система та сукупність рівнянь з однією змінною.

1. Розглянемо на множині Х два вирази із змінними і , які при деяких значеннях змінної можуть мати однакові значення.

Означення.1. Рівняння з однією змінною називається помісний предикат виду заданий на області визначення Х , для якого вимагається знайти ті значення змінної х , при якій предикат перетворюється в істинну числову рівність.

Розв’язати рівняння означає знайти значення змінної х , при якому предикат (тобто рівняння) перетворюється в числову рівність.

Оскільки рівняння є предикатом то з ним задано дві множини: 1) область визначення предиката – множина допустимих значень змінної; 2) область істинності предиката - множина коренів (або розв’язків ) рівняння. Причому множина коренів рівняння є підмножиною множини допустимих значень змінної, тобто .

2. Нехай на множині Х задано два рівняння і , нехай - відповідно множини їх розв’язків. Для множин і можливі такі співвідношення .

Означення 2. Два рівняння і задані на одній і тій самій області визначення Х називаються рівносильними, якщо всі розв’язки першого рівняння є розв’язками другого рівняння і навпаки, тобто множини їх розв’язків співпадають.

Рівняння, множини розв’язків яких порожні, також прийнято вважати рівносильними.

Означення 3. Якщо множини розв’язків рівняння є підмножиною множини розв’язків рівняння , то друге рівняння є наслідком першого(тобто, якщо кожен корінь першого рівняння задовольняє друге рівняння).

Інше означення рівносильних рівнянь:два рівняння називаються рівносильними тоді і тільки тоді, коли кожне з них є наслідком іншого.

При розв’язування рівнянь виконують заміну попереднього рівняння рівносильним йому, але простішого виду. Інколи доводиться переходити до нерівносильного рівняння, тобто його наслідна тоді множина розв’язків розширюється і потрібна перевірка коренів.

2. Теорема 1. Якщо до обох частин рівняння додати один і той самий вираз , який визначений на тій же області визначення Х, то дістанемо рівняння 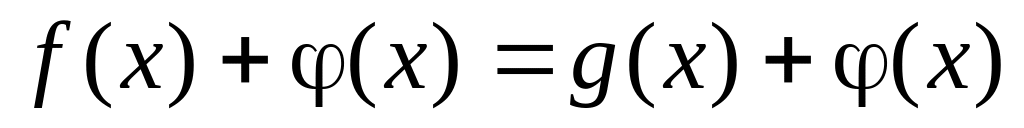яке рівносильне даному.

Доведення. Для доведення потрібно показати, що множина розв’язків обох рівнянь збігається . Позначимо - множина розв’язків рівняння (1); - множина розв’язків рівняння (2). Щоб показати, що , треба показати, що .

1) Нехай а довільний корінь рівняння (1), тоді - істинна рівність. Додамо до обох частин істинної рівності число і отримаємо істинну рівність , яка свідчить про те, що число а є коренем і другого рівняння. Оскільки а вибрано довільно, то .

2) Нехай b – довільний корінь рівняння (2), тому істинна рівність. Додамо до обох частин рівності число і отримаємо істинну рівність , свідчить, що число є коренем першого рівняння. Оскільки вибрано довільно, то . Отже, . Множини розв’язків рівнянь співпадають, тому рівняння рівносильні.

Наслідок 1. Члени рівняння можна переносити з однієї частини в іншу, змінивши при цьому їх знаки на протилежні.

Наслідок 2. Якщо у рівнянні в обох частинах є однакові вирази, то їх можна опустити.

Теорема 2. Якщо обидві частини рівняння заданого на множині Х помножити на однин і той самий вираз визначений на області визначення рівняння і який не перетворюється в нуль, то одержимо рівняння рівносильне даному.

Доведення. Аналогічне теоремі 1 (провести самостійно).

Наслідок 1. Якщо всі члени рівняння мають спільний множник, то на нього можна поділити всі члени (скоротити).

Приклад.

Наслідок 2. Якщо деякі члени рівняння є дробово-раціональними виразами, то помноживши рівняння на спільний знаменник цих дробів дістанемо рівняння з цими коефіцієнтами

Приклад 1) 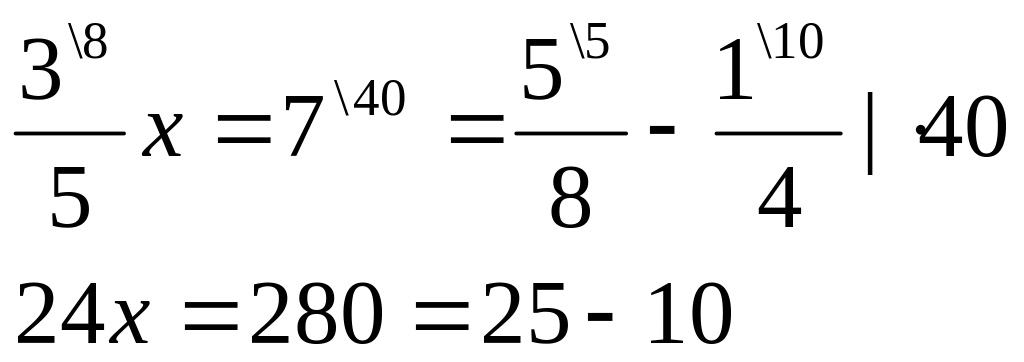2)

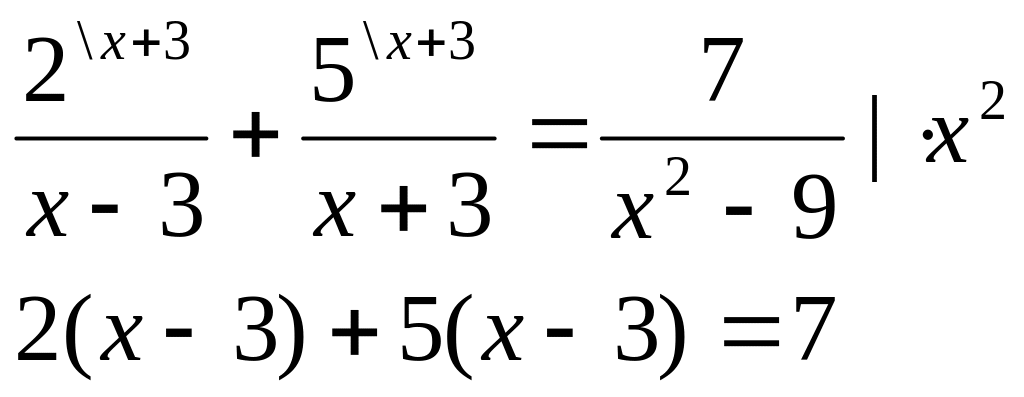
Якщо рівняння має вигляд , то множина розв’язків рівняння є об’єднанням множин розв’язків рівнянь

4. Означення 4. Системою 2-х рівнянь з однією змінною називають кон’юнкцію двох предикатів, задану на деякій області визначення , для якої вимагається знайти такі значення змінної , які перетворюють кожне з рівнянь в істину рівність.

Системи рівнянь з однією змінною розглядаються рідко, в основному з кількома змінними.

Означення 5. Сукупністю двох рівнянь з однією змінною називається диз’юнкція предикатів заданих на множині для якої вимагається знайти значення змінної , при яких хоча б одне з рівнянь перетворюється в істинну числову рівність.

Множина розв’язків системи – спільний розв’язок сукупності – об’єднання розв’язків.