
- •Тема1 Вирази
- •Властивості істинних числових рівностей
- •Властивості числових нерівностей
- •Тема 2 Функції
- •Властивості числових функцій
- •Властивості
- •Обернена пропорційність
- •Властивості
- •Геометричні зміни коефіцієнтів k та b лінійної функції
- •Різні способи задання прямої
- •Властивості
- •Перетворення графіків квадратної функції
- •Тема 3 Рівняння, їх системи та сукупності
- •Тема 4 Нерівності з однією змінною, їх системи та сукупності
- •Алгоритм розв’язування систем нерівностей
- •Алгоритм розв’язування сукупності нерівностей.
- •Тема 5 Рівняння з двома змінними
- •Алгебраїчні способи розв’язування систем рівнянь.
- •Тема 6: Нерівності з двома змінними
- •Тема 1: Геометричні побудови на площині
- •Тема 2: Многогранники та тіла обертання.
- •Тема 2: Величини та їх вимірювання.
Геометричні зміни коефіцієнтів k та b лінійної функції
1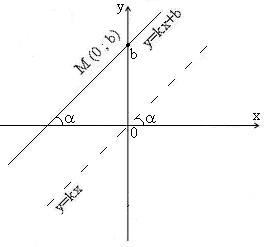 .У
формулі
.У
формулі
![]() значення
значення
![]() означає ординату точки перетину прямої
з віссю OY.
означає ординату точки перетину прямої
з віссю OY.
2. Для функції
число
![]() називається
кутовим коефіцієнтом
і виражає
називається
кутовим коефіцієнтом
і виражає
![]() кута нахилу прямої
до додаткового нахилу осі OX
. Оскільки прямі
і
паралельні, то кут нахилу до додатного
напряму осі OX
рівні як відповідні кути при перетину
перпендикулярних прямих січною. Отже,
кута нахилу прямої
до додаткового нахилу осі OX
. Оскільки прямі
і
паралельні, то кут нахилу до додатного
напряму осі OX
рівні як відповідні кути при перетину
перпендикулярних прямих січною. Отже,
![]() .
.
Означення.
Рівняння виду
![]() ,
де А, В, С – довільні числа називається
загальним рівнянням прямої (А,В,С –
коефіцієнти рівняння прямої).
,
де А, В, С – довільні числа називається
загальним рівнянням прямої (А,В,С –
коефіцієнти рівняння прямої).
Розглянемо різні випадки значень коефіцієнтів:
1).
![]() ;
;
![]() . Позначимо
. Позначимо
![]() отримаємо рівняння
.
отримаємо рівняння
.
Якщо коефіцієнт при х
і у
![]() 0,
а вільні члени дорівнюють 0, рівняння
виражає
пряму, яка проходить через початок
координат.
0,
а вільні члени дорівнюють 0, рівняння
виражає
пряму, яка проходить через початок
координат.
2).
![]()
![]() .
Позначимо
.
Позначимо
![]() ,
отримаємо
,
отримаємо
.
Якщо жоден з коефіцієнтів
![]() ,
то це рівняння виражає пряму, яка
перетинає обидві осі координат.
,
то це рівняння виражає пряму, яка
перетинає обидві осі координат.
3).![]() Позначимо
Позначимо
![]() .
.
Якщо коефіцієнт А=0, а інші не дорівнюють нулю, то це рівняння виражає пряму паралельну осі OX.
4).
![]()
![]()
Якщо коефіцієнт В=0, а інші не дорівнюють нуль, то загальне рівняння прямої виражає пряму паралельну осі OY.
5).
![]() - вісь OX.
- вісь OX.
6)![]() -
вісь OY.
-
вісь OY.
Легко бачити, що коефіцієнти А і В одночасно рівні нулю бути не можуть, бо тоді С=0 (одночасно).
Різні способи задання прямої
1. За даним кутовим коефіцієнтом і точкою, що належить прямій.
![]()
Оскільки точка належить
прямій, то її координати задовольняють
рівнянню пряма
![]() .
Звідси
.
Звідси
![]() .
Підставимо
в
(1)
.
Підставимо
в
(1)
![]() (2)
(2)
2. За двома точками, що належать
прямій
![]()
![]() .
.
Оскільки точки![]() і
і
![]() належать прямій, то координати
задовольняють рівнянню прямої:
.
належать прямій, то координати
задовольняють рівнянню прямої:
.
![]() .Отже,
.Отже,
![]() .
.
Підставимо у формулу (2) значення k:
![]() .
.
![]() -
рівняння прямої, що проходить через дві
точки.
-
рівняння прямої, що проходить через дві
точки.
5. Означення.
Квадратною називають функцію виду![]() ,
де a,b,c
деякі числа, причому
,
де a,b,c
деякі числа, причому
![]() .
Розглянемо властивості квадратної
функції на прикладі
.
Розглянемо властивості квадратної
функції на прикладі
![]() .
.
Властивості
Область визначення функції множина всіх дійсних чисел.
Область значень при а>0
 ,
при
,
при
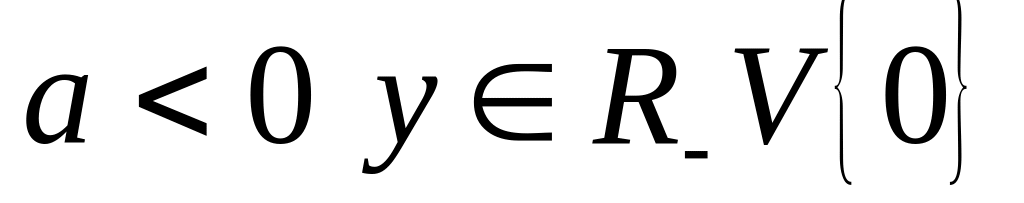 .
.Графіком функції є крива, яка називається параболою, вершина якої знаходиться в початку координат.
Функція є парною
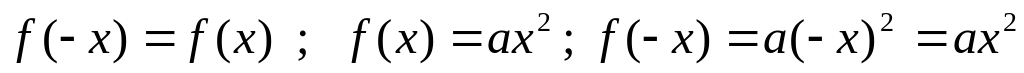 .
Парабола розташована симетрично
відносно осі OY.
.
Парабола розташована симетрично
відносно осі OY.П
 ри
а>0
функція спадає на проміжку
ри
а>0
функція спадає на проміжку
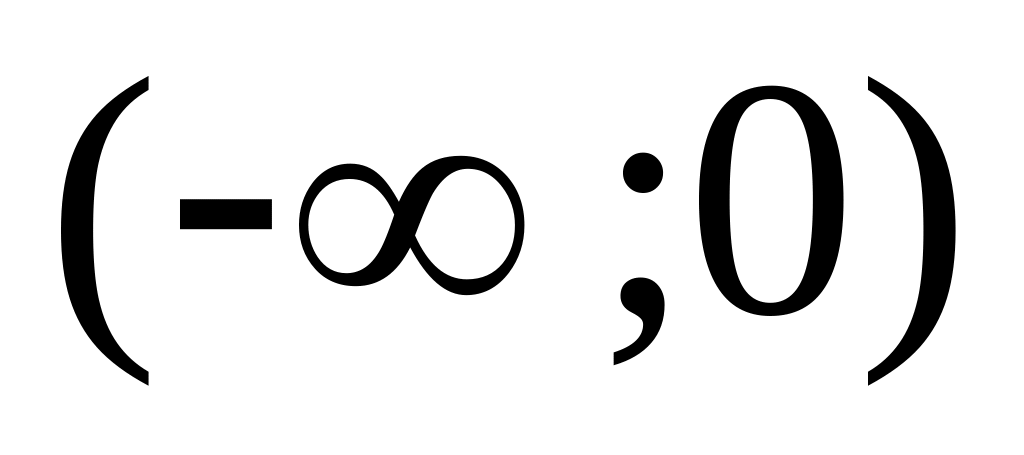 і
зростає на проміжку
і
зростає на проміжку
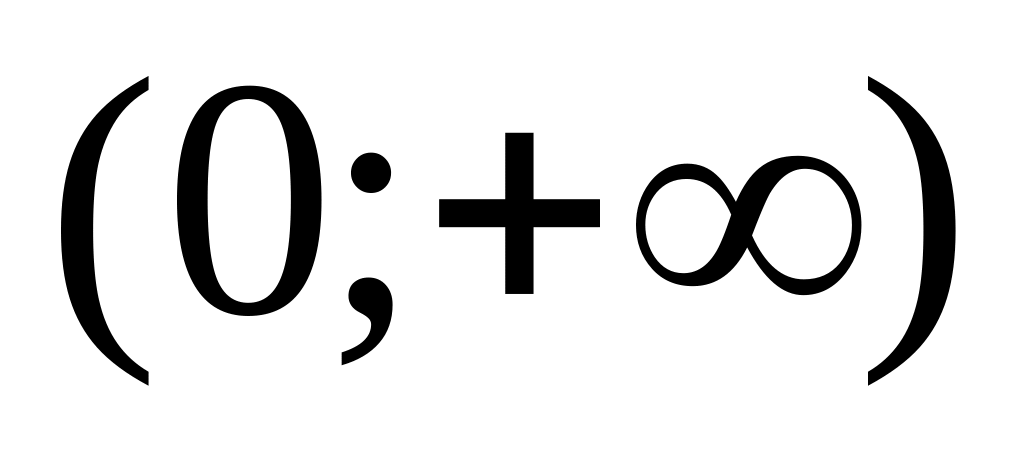 .
При
.
При
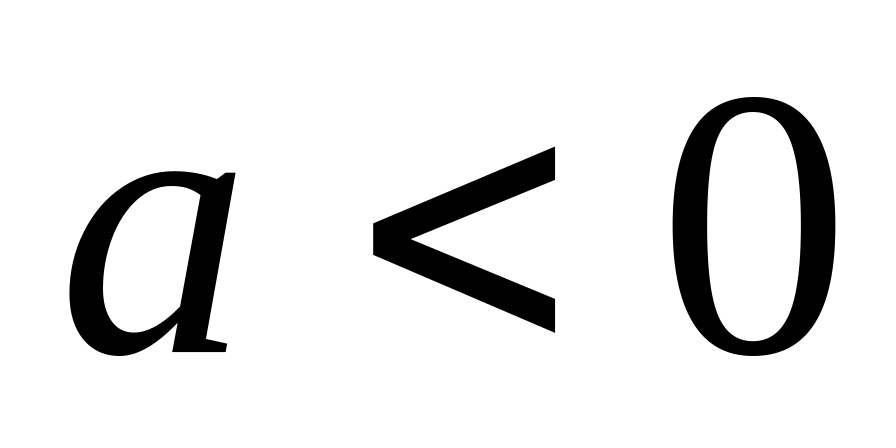 функція спадає на проміжку
функція спадає на проміжку
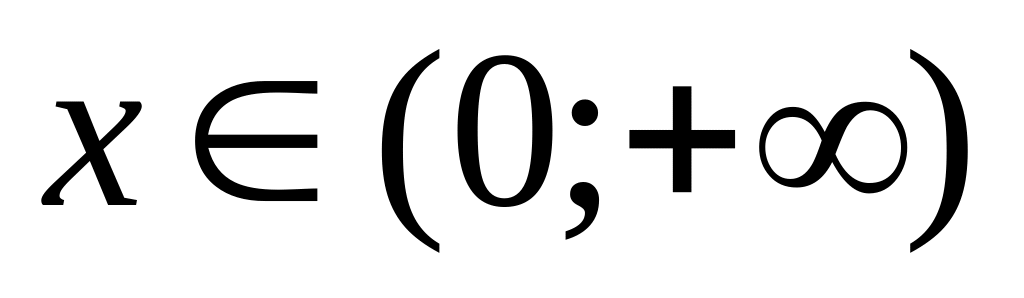 і
зростає
і
зростає
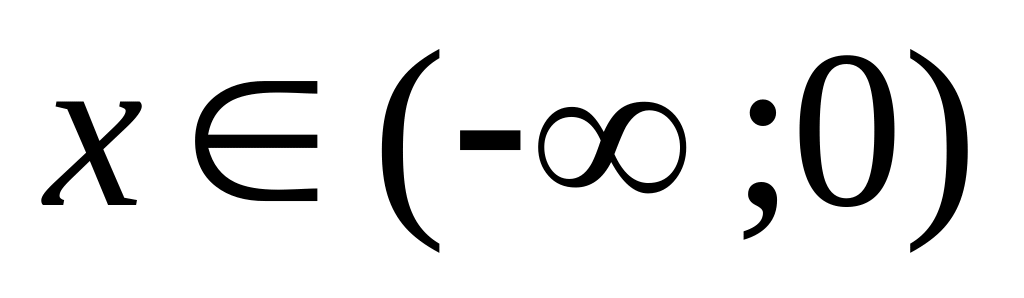 .
.При а>0 парабола розташована у верхній півплощині, при a<0– у нижній.
При а>0 функція обмежена знизу віссю OX , при a<0- зверху віссю ОХ.
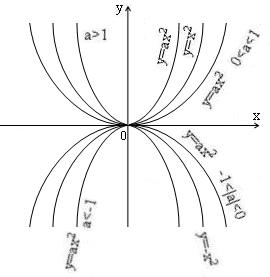
При
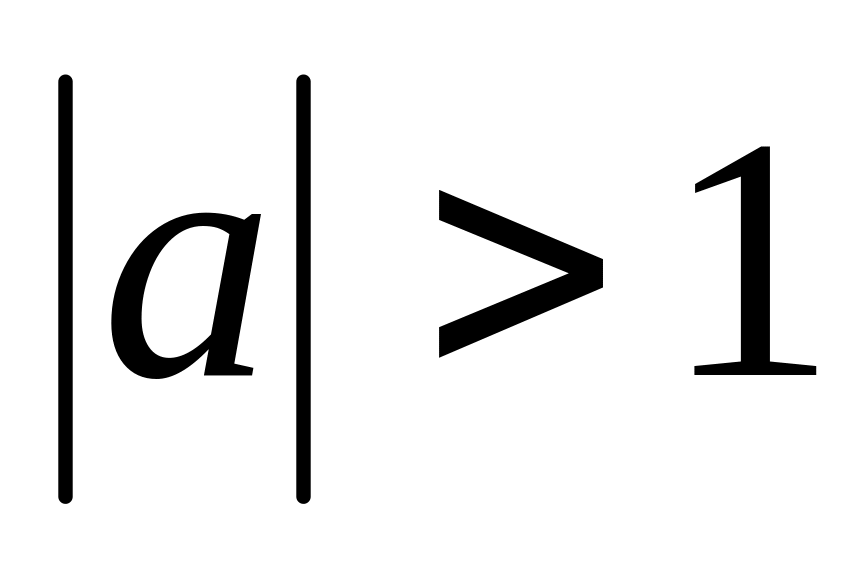 вітки параболи розташовані ближче до
осі OY,
при
вітки параболи розташовані ближче до
осі OY,
при
 вітки
розташовані ближче до осі OX.
вітки
розташовані ближче до осі OX.
9. Квадратна функція виду
має найбільше чи найменше значення,
якого досягає у вершині параболи
![]() .
При а>0
– найменше, a<0
– найбільше.
.
При а>0
– найменше, a<0
– найбільше.
Перетворення графіків квадратної функції
0. Графік функції
можна
отримати з графіка функції
![]() при
a>1
при
a>1
розтягом від осі OX,
при
![]() стиском
до осі OX.
стиском
до осі OX.
Легко бачити, що графік функції , при a<0 можна отримати з графіка функції при а>0 виконавши симетричне відображення відносно осі.
Графік функції
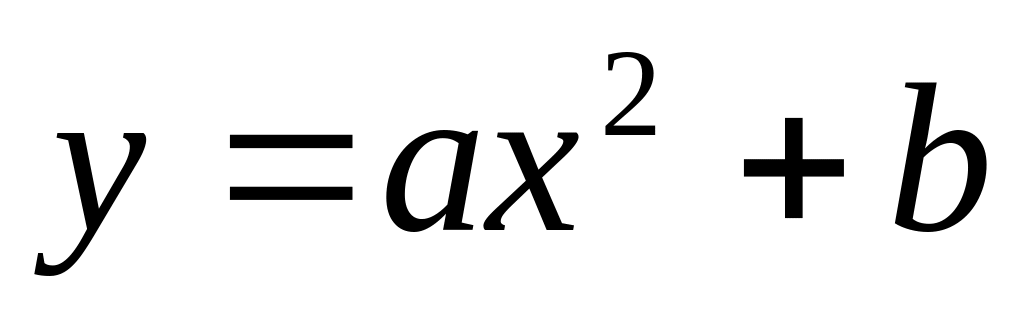 можна отримати з графіка функції
паралельним перенесенням вздовж осі
OY на b
одиниць вверх чи вниз залежно від знака
b (якщо
b>0↑,
b<0↓).
можна отримати з графіка функції
паралельним перенесенням вздовж осі
OY на b
одиниць вверх чи вниз залежно від знака
b (якщо
b>0↑,
b<0↓).Графік функції
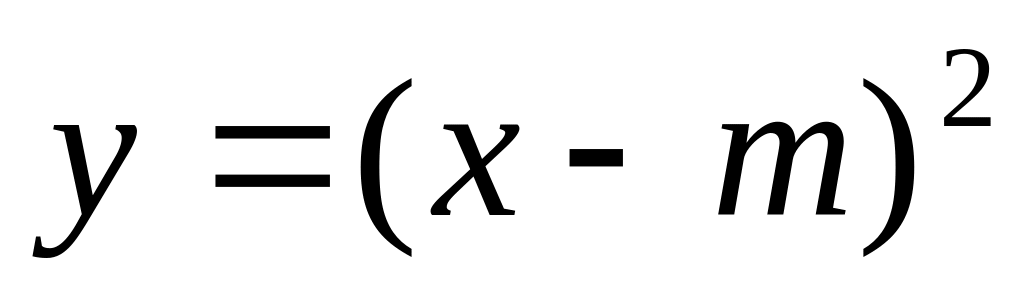 можна отримати з графіка функції
змістивши його вздовж осі OX
на m
одиниць вправо, якщо а>0
, вліво , якщо a<0.
можна отримати з графіка функції
змістивши його вздовж осі OX
на m
одиниць вправо, якщо а>0
, вліво , якщо a<0.Графік функції може бути отриманий з графіка функції , якщо її подати у вигляді
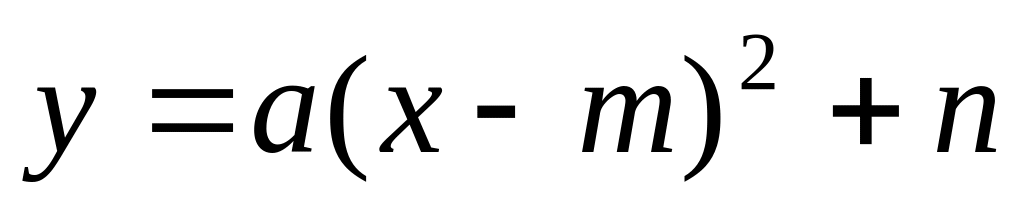 і
виконавши перетворення 1, 2, 3, 4.
і
виконавши перетворення 1, 2, 3, 4.
