Властивості числових функцій

Означення 5. Функція називається парною, якщо її область визначення симетрична відносно початку координат і для будь – якого х з області визначення виконується рівність .

Означення 6. Функція називається непарною, якщо її область визначення симетрична відносно початку координат і для будь-якого х з області визначення виконується рівність .

Графіки непарних функцій симетричні відносно осі координат, а непарних функцій – відносно початку координат.

Означення 7. Функція називається зростаючою, якщо більшому значенню аргумента відповідає більше значення функції: .

Означення 8. Функція називається спадною, якщо більшому значенню аргумента відповідає менше значення функції: .

2. Означення 9. Дві величини називаються прямо пропорційними, якщо збільшенням (зменшенням) однієї величини у кілька разів у стільки ж разів збільшується (зменшується) інша величина при сталій третій величині.

Приклад: υ і S при сталій t. Кількість і вартість при сталій ціні.

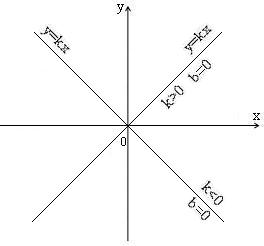
Означення 10. Прямо пропорційною називають функцію виду , де k – стала величина, , а х – незалежна змінна.

Графіком прямо пропорційності є пряма, яка проходить через початок координат.

Властивості

1. Область визначення

2. При k>0 функція зростає на всій області визначення, при k<0 спадає.

3. Положення в системі координат залежить від:

при k>0 в I і III чверті;

при k<0 в II і IV чверті.

4. Функція є непарна: . Її графік симетричний відносно початку координат.

5. Графік функції проходить через точку (1; k)

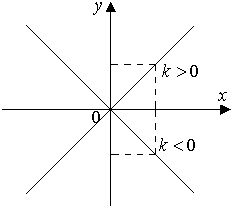
6. При 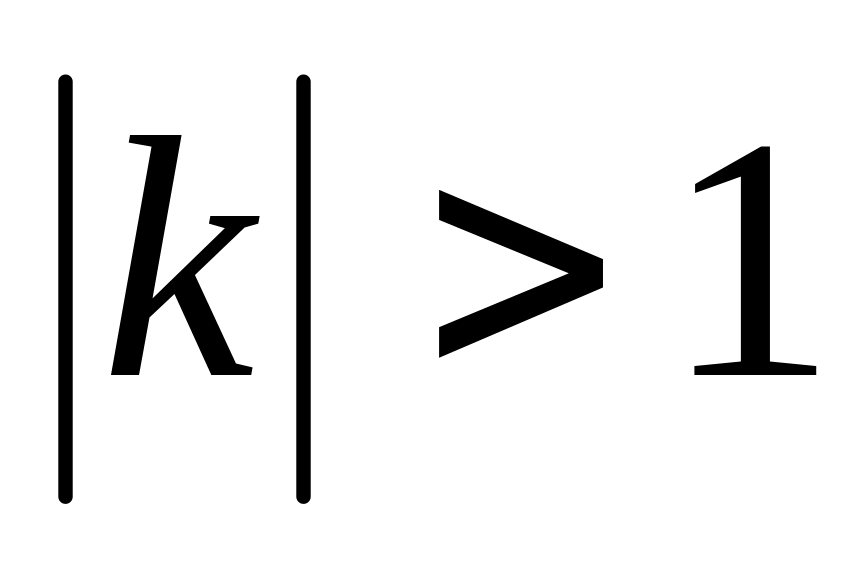наближається графік до осі OY;

графік наближається до осі OX

Обернена пропорційність

Означення. Дві величини x та y перебувають в обернено пропорційній залежності тоді, коли із збільшенням (зменшенням) значення однієї з них у кілька разів значення другої величини зменшується (збільшується у стільки ж разів) при сталій третій величині.

Приклад: υ і t при при сталій відстані. Ціна і кількість при сталій вартості.

Означення. Обернено пропорційністю називається функція виду , де k – стала величина, і називається коефіцієнтом оберненої пропорційності, х – незалежна змінна, де - залежна змінна, де .

Отже, область визначення і область значень оберненої пропорційності є множина всіх дійсних чисел, крім нуля.

Розглянемо властивості функції на прикладі :

х	-8	-4	-2	-1	1	2	4	8
y	-1	-2	-4	-8	8	4	2	1

Графіком функції є крива, що складається з двох віток і називається гіперболою.

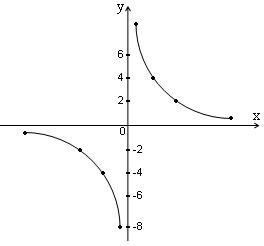
Властивості

1.Функція розривна в точці х=0.

2. Положення гіперболи в системі координат залежить від k : при k>0 графік розміщений в І і ІІІ чверті; при k<0 вітки розміщені в II i IV чверті.

3. Графік розміщено симетрично відносно початку координат. Функція є непарною: . Отже, .

4. При вітки гіперболи глибше вгнуті до початку координат, чим більше k ; при вітки більше віддалені від початку координат.

5. При функція спадна ;

При функція є зростаючою .

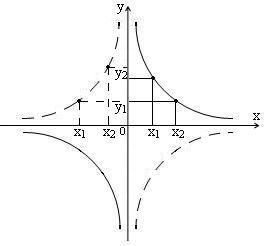
6. Функція неперіодична, бо не існує такого числа Т , що .

7. Функція обмежена: при ліва вітка обмежена зверху, а права знизу; при ліва вітка обмежена знизу, а права зверху. В обох випадках вітки обмежені прямої (віссю ОХ) і х=0 (віссю OY). Отже осі координат є асимптотами даної функції.

Означення. Асимптотою деякої функції називають пряму, до якої як завгодно близько підходить графік функції але піком її не перетинає та не дотикається.

4. Означення. Лінійною функцією називають функцію виду y = kx+b, де k i b – сталі, х- незалежна змінна. При b=0, отримаємо функцію y=kx – пряму пропорційність. Отже, пряма пропорційність є частковий випадок лінійної функції.

Графік лінійної функції є пряма, яка утворена з прямої паралельним перенесенням на b одиниць вздовж осі OY вверх, якщо і вниз, якщо .

Положення графіка функції визначається числами k i b.

а) б)

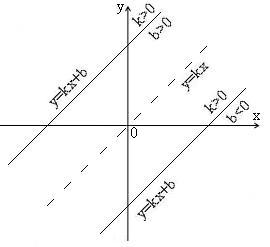
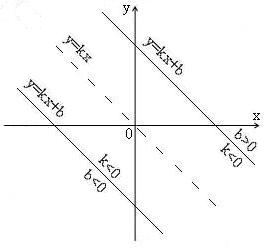
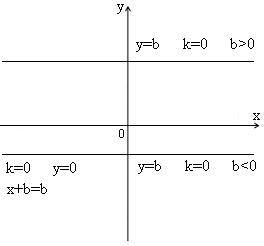в) г)

Якщо , а , то графіком лінійної функції є пряма , яка паралельна осі абсцис ОХ, причому, якщо , то пряма розташована у верхній півплощині, якщо - нижній півплощині. Всі точки прямої мають одну і ту ж саму ординату.

Якщо пряма паралельна до осі OY то всі її точки мають однакові абсциси, а ординати різні. Рівняння прямої паралельної до осі OY має вигляд х=а.