Тема 2: Величини та їх вимірювання.

План

1. Поняття величини як відображення властивостей реального світу.

2. Основні види величин. Основні властивості скалярних величин.

3. Поняття про вимірювання величин.

4. Поняття довжини відрізка, способів її вимірювання, одиниць вимірювання та співвідношень між ними.

5. Поняття площі плоскої фігури, її властивості, способів вимірювання, одиниць вимірювання та співвідношень між ними.

6. Площа прямокутника та деяких інших многокутників. Рівновеликі та рівноскладені многокутники.

7. Площі поверхонь тіл.

8. Поняття об’єму тіла, його властивостей, способів вимірювання, одиниць вимірювання та співвідношень між ними.

9. Об’єм многогранників та тіл обертання.

« 1 »

Величини відображають різноманітні властивості реального світу. Поняття величини, виникло в результаті абстрагування від якісних особливостей, властивостей реальних об’єктів, щоб виділити тільки кількісні відношення. У процесі абстракції властивості об’єктів і явищ ідеалізуються, відбувається деяке віддалення від дійсності. У природі величини не існують відірвано від матеріальних об’єктів. Наприклад, не існує довжини, площі, сили, швидкості. Ці величини вводяться в процесі пізнання для опису явищ природи. Тому Величина – це не сама реальність, а лише її відображення. Поняття величини тісно пов’язане з поняттям вимірювання. Результат вимірювання виражається числовим значенням величини при певній одиниці вимірювання. Величини є складовою частиною змісту багатьох наук – математики, фізики, хімії, біології та ін. Без величин вивчення природи обмежилось би тільки спостереженнями і залишилося б на описовому рівні. Величини дають можливість перейти від описового до кількісного вивчення властивостей об’єктів.

« 2 »

До ХVІІ ст. предметом вивчення математики були сталі величини, після ХVII ст. – змінні величини. Усю сукупність величин за певними характеристичними властивостями поділяють на такі величини: скалярні, векторні, латентні та ін. В математиці і фізиці розглядають скалярні і векторні величини.

Скалярні величини – це величини, які повністю характеризуються числом.

Приклад: довжина, маса, площа, об’єм, густина та ін.

Векторні величини – це величини, які характеризуються не тільки числом, але й напрямком. Приклад: швидкість, прискорення, сила та ін.

Геометрично векторні величини зображуються напрямними відрізками, які не можна виміряти називаються латентними. Приклад: горе, воля, щастя, радість, гнів тощо. Далі будемо розглядати лише скалярні величини.

Означення 1 Однорідними величинами називається величини, які характеризують ту саму якість об’єктів.

Властивоті однорідних величин:

1) Еквівалентності (рефлексивність, симетричність, транзитивність).

2) Порядку Будь-які дві величини одного роду можна порівнювати, тобто для

будь-яких однорідних величин a і b справедливе одне і тільки одне співвідношення а<b, а=b, а>b.

3) Величини одного роду можна додавати, одержуючи в результаті величину того ж роду.

4) Величину можна множити на дійсне число, одержуючи в результаті того ж роду.

5) Величини одного роду можна віднімати.

6) Величини одного роду ділять, отримуючи в результаті дійсне число а/b=х, хєR.

« 3 »

Одним із важливих завдань при вивчені величини є завдання вимірювання величин. Спільним при вимірюванні будь-яких величин є те, що вимірювання завжди є порівняння величини даного роду з певною величиною цього ж роду, взятого за одиницю вимірювання, і вираження результату порівняння числом.

Нехай маємо величину Ф певного роду. Візьмемо величину е цього ж роду за одиницю вимірювання. Якщо величину Ф можна розбити на n рівних частин, кожна з яких дорівнює е, то кажуть, що число n є мірою величини Ф і позначається M_e(Ф)=n або Ф=n·е.

Число n може бути не лише цілим, а й дробовим.

Означення 2 Мірою величини Ф називають число m(Ф), поставлене у відповідність величині Ф так, що виконуються такі вимоги:

1) міра будь-якої величини Ф невід’ємна: m(Ф)≥0;

2) рівні величини мають рівні міри: Ф₁=Ф₂→m(Ф₁)=m(Ф₂);

3) міра величини Ф дорівнює сумі мір величин, на які можна розбити дану величину: Ф=Ф₁+Ф₂+...+Ф_n→m(Ф)=m(Ф₁)+m(Ф₂)+...+m(Ф_n).

4) деяка величина е того самого роду, що й величина Ф, має міру, яка дорівнює одиниці: m(е)=1. Величина е називають одиницею вимірювання величин Ф.

Наведені вимоги називають аксіомами міри величини Ф.

Наслідок Більша величина має більшу міру.

« 4 »

Означення 3 Довжиною відрізка називається додатна величина, визначена для кожного відрізка так, що:

1) рівні відрізки мають рівні довжини;

2) якщо відрізок складається із скінченого числа відрізків, то його довжина дорівнює сумі довжин цих відрізків;

3) існує відрізок, довжина якого дорівнює одиниці.

Наведені умови називають властивостями або аксіомами довжини. Визначена таким чином довжина відрізка задовольняє властивості рефлексивності, симетричності та транзитивності, тому розбиває множину всіх відрізків на класи рівних відрізків.

Завдання вимірювання довжини відрізка полягає у послідовному відкладанні одиничного відрізка і його частин на даному відрізку, довжину якого треба виміряти. Процес вимірювання довжини відрізка грунтується на аксіомі Архімеда:

Нехай маємо два відрізка АВ і РМ, причому АВ>РМ. Який би не був великий відрізок АВ і який би не був малий відрізок РМ, завжди знайдеться таке натуральне число n, що n РМ>АВ.

На основі аксіоми Архімеда кожному відрізку АВ при вибраній одиниці довжини е можна поставити у відповідність певне невід’ємне число, яке є його довжиною. Для доведення оберненого твердження необхідна аксіома Кантора.

Нехай на довільній прямій МК дано нескінчену послідовність відрізків

А₁В₁, А₂В₂, ... ,А_nВ_n, ... таку, що: 1) кожний наступний відрізок є частиною попереднього; 2) для будь-якого попереднього заданого відрізка СD знайдеться натуральне число n таке, що А_nВ_n<CD.

Тоді на прямій МК існує єдина точка Р, що належить усім відрізкам послідовності.

Розглянуті аксіоми дають можливість довести твердження про те, що між множиною відрізків і множиною невід’ємних дійсних чисел існує взаємооднозначна відповідність.

Основою встановлення системи вимірювання довжин відрізків, як і інших величин, є вибір зручних, чітко визначених одиниць вимірювання та точність виготовлення еталонів цих одиниць. Основою для міжнародної системи мір стала система одиниць вимірювання величин створена у Франції у ХVIII ст. За основну одиницю довжини в ній було взято метр – одна сорокамільйонна частиеа довжини земного меридіана, який проходить через Париж.

Еталон 1м виготовлений із сплаву платини та у вигляді лінійки з штрихами і зберігається у Міжнародному бюро міри і ваги Національного архіву Франції. Були також введені похідні одиниці довжини: 1см=1/100м; 1дм=1/10м; 1мм=1/1000м; 1км=1000м. Нову систему мір назвали Метричною.

Наведемо приклади неметричних одиниць довжини:

1миля=7верств;

1верства=500саженів=1,0668км;

1сажень=3аршини=7футів=2,1336м;

1аршин=16вершнів=71,12см;

1фут=12дюймів=0,3048м;

1дюйм=1/12 фута=2,54см;

1вершок=1^3/4дюйма=4,45см.

« 5 »

Візьмемо на площині прямокутну систему координат хОу з одиничним відрізком е на осях ОХ і ОУ. Через точки поділу проведемо прямі, паралельні осям координат. При цьому координатна площина покриється сіткою квадратів зі стороною е. Площа кожного такого квадрата дорівнює 1. Кажуть, що площина покрита сіткою квадратів нульового рангу.

Поділимо далі одиничні відрізки на 10 рівних частин і достанемо відрізки е₁=1/10е.

Провівши через нові поділки прямі, паралельні осям ОХ і ОУ, покриємо координатну площину сіткою квадратів першого рангу. У кожному квадраті нульового рангу міститься 100 квадратів першого рангу. Аналогічно можна одержати сітку квадратів 2-го, 3-го,..., n-го рангів зі сторонами е₂=е₁/10=е/10²; е₃=е₂/10=е/10³; .... , е_n=е_n-1/10=е/10ⁿ. Приклад, такої сітки – міліметровий папір.

Означення 4 Фігура F називається квадратною, якщо вона повністю покривається ступінчастою фігурою, утвореною з квадратів сітки, і якщо існує хоча б один як, завгодно малий квадрат з покриття, який повністю складається з внутрішніх точок фігури F.

Якщо ці умови не виконуються, то площа фігури дорівнює нулю.

С тупічаста фігура Ф, утворена з квадратів сітки, яка у

повністю покриває фігуру F, називається фігурою Ф

покриття фігури F. F

О х

Квадрати фігури покриття Ф поділяють на дві групи:

1) квадрати, утворені тільки внутрішніми точками фігури F і точками її контура;

2) квадрати, які містять як внутрішні, так і зовнішні точки фігури F.

Площу фігури F можна знайти, порахувавши квадрати. Якщо внутрішні квадрати нульового рангу не вичерпують фігури F, то переходимо до квадратів першого рангу і т.д.

Означення 5 Площею фігури називається невід’ємна скалярна величина, яка характеризує міру квадратності і має такі властивості:

1) Існує квадрат, площа якого дорівнює 1; це квадрат, сторона якого є одиницею довжини.

2) Рівні фігури мають рівні площі.

3) Якщо фігура складається з кількох частин без спільних внутрішніх точок, то їх площа дорівнює сумі площ цих частин.

Прилад, з допомогою якого таким способом вимірюють площу фігури, називається палеткою – прозора пластина з нанесеною на ній сіткою квадратів.

Метричні міри площі та співвідношення між ними:

1м²; 1дм²=0,01м²; 1а=100м²;

1см²=0,0001м²; 1ге=10000м²;

1мм²=0,000001м²; 1км²=1000000м².

Означення 6 Два многокутники, які мають рівні площі, називаються рівновеликими.

Зауважимо, що рівновеликі многокутники можуть бути й не рівними. Наприклад, прямокутники зі сторонами 4·6=24см², 2·12=24см² нерівні, але рівновеликі.

Означення 7 Два многокутники називаються рівноскладеними, якщо їх можна розкласти на одне й те саме число попарно рівних многокутників. Відношення рівноскладеності многокутників має властивості рефлексивності, симетричності і транзитивності, тобто є відношенням еквівалентності.

Теорема 1 Будь-які два рівноскладені многокутники рівновеликі і навпаки.

Т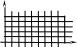 еорема 2 Площа прямокутника дорівнює добутку довжин його суміжних сторін; S=ab. у

Доведення: Розглянемо прямокутник у системі координат, А С

яка вибрана так, щоб осі ОХ і ОУ проходили через суміжні b

сторони прямокутника. Нехай АВ=b·а, АD=a·e. x

Прямокутник складається з а вертикальних стовпців, A a D

у кожному з яких b квадратів нульового рангу. Отже, число квадратів = а·b; S=ab

Якщо довжини сторін не виражаються цілими числами, то перейшовши до квадратів 2-го, 3-го і т.д. рангу отримаємо S=a·b.

Т еорема 3 Площа прямокутного трикутника дорівнює А D

півдобутку катетів.

Доведення: Добудуємо ΔАВС до прямокутника b

ADBC: ΔABD=ΔABC→S_ΔABD=S_ΔABC

S_ADBC=2S_ΔABC S_ΔABC=1/2S_ADBC=1/2ab. C B

Теорема 4 Площа паралелограма дорівнює добутку

с торони на висоту, яка проведена до цієї сторони. B C

Доведення: Паралелограм ABCD рівноскладений з h

прямокутником НВСК (ΔАВН=ΔDCK)

S_ABCD=S_HBCK=BH·BC; S=a·h.

A H a D K

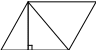
Теорема 5 Площа трикутника дорівнює половині B D

добутка основи на висоту.

Доведення: Добудуємо ΔАВС до паралелограма ABDC. h

ΔАВС=ΔDCB; S_ΔABC=1/2 S_ABDC=1/2 a·h

A a C

Т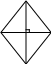 еорема 6 Площа ромба дорівнює половині B

добутку діагоналей.

Доведення: ΔАВС=ΔADC;

S_ABCD=2S_ΔABC=2·1/2AC·BO=AC·BO=AC·1/2BD=1/2d₁·d₂ A O C

D

Теорема 7 Площа трапеції дорівнює добутку

півсуми її основ на висоту. B b C

Д оведення: S_ABCD=S_ΔABC+S_ΔACD

S_ΔABC=1/2BC·h; S_ΔACD=1/2AD·h; h

S_ABCD=1/2BC·h+1/2AD·h=1/2h(BC+AD)

S=a+b/2·h A a n D

Наведемо деякі формули для обчислення площ плоских фігур.

Площа трикутника: S=1/2ah; S=1/2ab·sinγ

S=√p(p-a)(p-b)(p-c) (Ф – ла Герона) p=a+b+c/2

S=abc/4R; S=1/2Pr

Площа паралелограма: S=ah; S =ab sinI;

S=1/2d₁·d₂·sinφ

Площа круга: ПR²

Площа ромба: S=ah; S=1/2d₁d₂

Площа трапеції: S a+b/2·h; S=m·h, m-середня лінія.

« 7 »

Площею поверхні многогранника називається сума площ усіх його граней. Площею бічної поверхні призми і піраміди називають суму площ всіх їх бічних граней.

Теорема 8 Площа бічної поверхні довільної призми дорівнює добутку периметра перпендикулярного перерізу призми на її бічне ребро.

Наслідок Площа бічної поверхні прямої призми дорівнює добутку периметра її основи на довжину бічного ребра. S_б.пр=P·H

Площа бічної поверхні піраміди дорівнює сумі площ її бічних граней.

Теорема 9 Площа бічної поверхні правельної піраміди дорівнює половині добутку периметра її основи на довжину апофеми. S_б.пір=1/2P·l

Теорема 10 Площа бічної поверхні циліндра дорівнює добутку довжини кола його основи на висоту, тобто S_б.ц=2ПRH

S_п.ц=S_б+2S_o=2ПRH+2ПR²=2ПR(H+R)

Теорема 11 Площа бічної поверхні конуса дорівнює половині добутку довжини кола основи на довжину твірної, тобто S_б.к=ПRL, L-твірна конуса S_п.к=S_б+S_o=ПRl+ПR²=ПR(l+R)

Теорема 12 Площа поверхні кулі дорівнює почетвертій площі її великого круга: S_кр=4ПR²

« 8 »

Означення 8 Об’ємом геометричного тіла називають величина обмеженої частини простору, займає тіла. Аналогічно, як і для поняття площі, вводиться система координат, одиничний відрізок і простір розбивається на куби, ребро кожного з яких дорівнює одиниці довжини. Об’єм такого куба приймається за одиницю. Тоді об’єм тіла виражається числом одиничних кубів, на які розбите дане тіло.

Властивості об’єму тіла:

1) Рівні тіла мають рівні об’єми.

2) Якщо тіло розбито площиною на частини, то об’єм цього тіла дорівнює сумі об’ємів утворених частин.

3) Існує тіло, об’єм якого дорівнює одиниці.

Ці властивості називають аксіомами об’єму тіла. За одиницю об’єму приймають об’єм куба, ребро якого дорівнює одиниці довжини.

Одиниці вимірювання об’єму:

1м³=1000дм³; 1см³=1000мм³;

1дм³=1000см³; 1л=1дм³.

Означення 9 Два тіла називаються рівноскладеними, якщо з усіх частин одного тіла можна скласти друге тіло.

Означення 10 Тіла, які мають рівні об’єми, називаються рівновеликими.

Рівноскладені тіла є одночасно і рівновеликими. Обернене твердження не виконується.

« 9»

Теорема 13 Об’єм прямокутного паралелепіпеда дорівнює добутку трьох його вимірів. V=abc

Наслідок 1 Об’єм куба дорівнює кубу його ребра.

Наслідок 2 Об’єм прямокутного паралелепіпеда дорівнює добутку площі основи паралелепіпеда на висоту. V=S_o·H.

Наслідок 3 У прямокутного паралелепіпеда будь-яку грань можна прийняти за основу.

Теорема 14 Об’єм призми дорівнює добутку площі її основи на висоту. V_пр=S_o·H

Наслідок 1 Призми, які мають рівновеликі основи і рівні висоти – рівновеликі.

Теорема 15 Об’єм піраміди дорівнює третині добутку площі її основи на висоту. V_пір=1/3S_o·H

Теорема 16 Об’єм циліндра дорівнює добутку площі його основи на висоту. V_ц=S_o·H=ПR²H

Теорема 17 Об’єм конуса дорівнює одній третій добутку площі його основи на висоту. V_к=1/3 S_о·H=1/3ПR²H

Теорема 18 Об’єм кулі дорівнює добутку однієї третини поверхні кулі на її радіус.

V_кулі=1/3 S_сер·R=4/3 ПR³

Наслідок Об’єми куль відносяться як куби їх радіусів.