Тема1 Вирази

1. Числові вирази, їх види. Значення числового виразу та порядок обчислення значення числового виразу.

2. Числові рівності та нерівності, їх властивості.

3. Вираз із змінною, область визначення. Тотожності, тотожні перетворення виразів.

1. У математиці під числовою алгеброю розуміють таку алгебру, основною множиною якої є числа і букви, основними операціями якої є додавання, віднімання множення і ділення З елементів основної множини за допомогою операцій утворюють інші елементи числової алгебри.

Мова будь-якої алгебри складається з множини знаків, яку називають алфавітом цієї мови. Числова алгебра містить десять цифр 0,1,2,3,4,5,6,7,8,9. За допомогою цифр утворюють назви будь-яких чисел. Для позначення числових змінних використовують букви латинського алфавіту або букви з індексами .Початкові букви використовуються для позначення чисел, а останні букви алфавіту для позначення змінних. Для позначення операцій використовують знаки “+”, “-”, “∙”, “:”, а також використовують дужки.

Отже, алфавіт мови будь-якої числової алгебри вимагає таку множину . Із елементів множини А утворюють скінченні послідовності цифр, букв, які над виразами. Однак, не кожна послідовність цифр і букв алфавіту А є виразом. Наприклад 5-) не є виразом.

Означення 1.1. Кожна окрема цифра або буква латинського алфавіту є виразом. Такі вирази називаються елементарними.

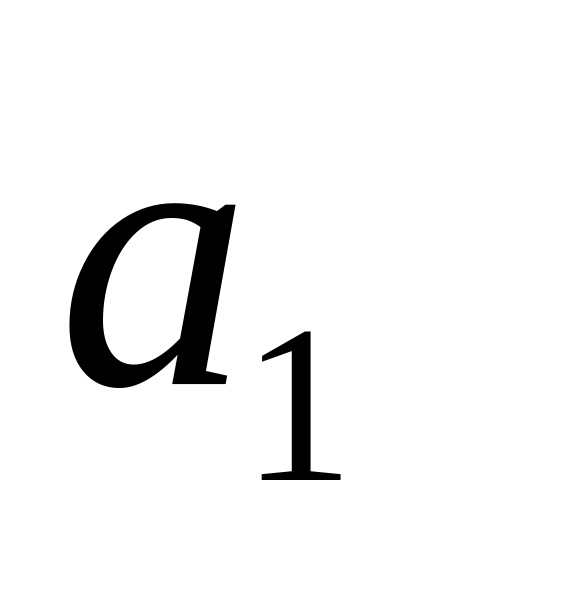2. Якщо і 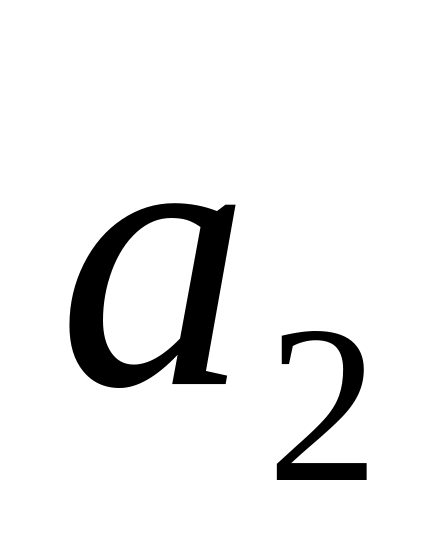вирази, то також вирази.

3. Інших виразів, крім тих, що у п.1і 2 не існує.

Для спрощення запису виразів прийняли такі домовленості:

а) опускати зовнішні дужки;

б) у виразі повинна бути однакова кількість правих і лівих дужок;

в) вважати, що знак множення пов’язує сильніше ніж знак додавання.

Наприклад . Чи є виразом послідовність букв . Має бути

Вирази поділяють на числові і не числові.

Означення 2. Вираз, який не містить змінних, тобто складається тільки з цифр, знаків операції і дужок, називається числовим виразом.

Приклад: 7; (2+8)∙7-5.

Якщо виконати відповідні функції у виразі, ми отримаємо число, яке називається значенням числового виразу. Існують числові вирази, які у певній множині не мають числового значення. Наприклад (5-3):3 у множині натуральних чисел не має числового значення, але в множині раціональних чисел його числове значення .

2. Означення 3. Два числових вирази сполучені знаком рівності називається числовою рівністю.

Числова рівність може бути істинною і хибною, залежно від того чи рівні їх числові значення.

Властивості істинних числових рівностей

Властивість 1.Якщо , істинна числова рівність , а с – будь-яке дійсне число, то також числова рівність.

Якщо до обох частин істинної числової рівності додати одне й те ж саме дійсне число, то знову одержимо істинну числову рівність. Ця властивість дозволяє перемістити числа з однієї частини рівності в іншу, змінивши їх знак на протилежний.

Властивість 2. Якщо - істинна числова рівність і с – будь-яке дійсне число, крім 0, то також істинна числова рівність.

Якщо обидві частини істинної числової рівності помножити на одне й теж саме, відмінне від нуля дійсне число, то одержимо істинну числову рівність.

Означення 4. Два числових вирази, сполучені одним із знаків утворюють висловлення , яке називається числовою нерівністю.

Приклад: 27-14>4:3.

Числові нерівності бувають, так як і висловлення, істинними або хибними.

Нерівності a>b i c>d (або a<b i c<d…) називаються нерівностями одного знаку. Нерівності a>b i c<d – нерівностями протилежного знаку. Нерівності a>b, c<d називаються строгими нерівностями, нерівності нестрогими. Кажуть a>b, якщо ; , якщо ; , якщо