16 Применение позиционного регулирования пид-регуляторов. Способы технической реализации систем регулирования
ПИД – регулятор вырабатывает выходной сигнал равный сумме трех составляющих П(пропорционального регулирования) + И(регулирование по интегралу) + Д(регулирование по производной). Уравнение классического ПИД-регулятора:
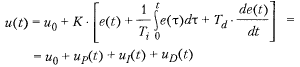
up(t) – разность между выходной величиной опорным значением, uI(t) – интеграл по времени ошибки выходной величины, uD(t) – производная ошибки. К – коэффициент усиления регулятора, Ti – постоянная времени интегрирования, Td – постоянная времени дифференцирования, u0 – поправочное значение (или смещение), настраивающий средний уровень выходного сигнала регулятора. Параметры К, Ti, Td – можно настроить с помощью ручек на панели управления регулятора. К – может быть безразмерным (но иногда в технических единицах; например, расход – м3 *с-1).
Классический регулятор – теоретическая конструкция, которую точно нельзя воспроизвести на практике. С математической точки зрения, выходной сигнал такого регулятора не ограничен, а выход реального регулятора будет ограничен некоторыми пределами umin, umax (рисунок).
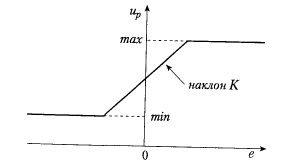
Интегральная часть используется для устранения стационарных ошибок. Если замкнутая система, состоящая из физического процесса и регулятора, достигла стационарного состояния, все ее сигналы e(t), u(t) постоянны. Стационарное состояние может сохранятся лишь при условии, что интегральная часть u(t) постоянна, а иначе будет изменятся. Соответственно интегральная часть остается постоянной лишь при e(t)=0.
Т.к. ПИД-регулятор представляет систему второго порядка, то его можно применять для управления процессами с динамикой второго порядка.
В некоторых системах управления процессами опорное значение время от времени резко изменяется, а между скачками остается постоянным. Скачек опорного значения приводит к резкому изменению выходного сигнала регулятора, этот эффект «всплеском производной».
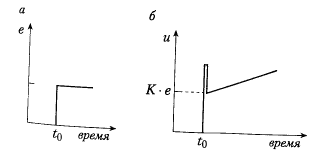
Переходная характеристика ПИД – регулятора: а - скачок ошибки происходит в момент t0; б -дифференциальная часть регулятора – причина всплеска в величине выходного сигнала;
При реализации регулятора необходимо принимать много различных факторов. Нужно разработать дискретную модель регулятора должна быть «реалистичной», т.е. находится между минимальным и максимальными значениями. Кроме этого должен быть ограничен не только выходной сигнал, но и скорость его изменения из-за физических возможностей исполнительных механизмов и черезмерного износа. Изменение настроек параметров и переключение с автоматического режима работы на ручной или другие изменения условий эксплуатации не должны приводить к возмущениям регулируемого процесса.
Регуляторы можно создать по аналоговой технологии на базе операционных усилителей или как цифровые устройства на основе микропроцессоров. Несмотря на то что цифровая технология имеет много преимуществ, аналогового подход по прежнему сохраняет свои позиции, т.к. он является основой для цифровых решений.
Существует два типа алгоритма регулятора – позиционный и приращений.
В позиционном алгоритме выходной сигнал представляет собой абсолютное значение управляющей переменной исполнительного механизма. Дискретный ПИД – регулятор имеет вид:
Интеграл аппроксимируется конечными разностями:
с постоянной
.
Величина второго слогаемого при малых
h и больших Ti
может стать очень мальнькой, поэтому
нужно позаботиться о том, чтобы обеспечить
необходимую точность его машинного
представления.
Дифференциальная часть ПИД-регулятора:
Если постоянная времени дифференциального члена Td = 0, следовательно дифференцирование описывается простой разностной аппроксимацией выходного сигнала dy/dt.
Системы двухпозиционного регулирования
Они имеют в своем составе двухпозиционный или Пз-регулятор, выходная величина которого может принимать только два значения, максимальной хmax и минимальной xmin величинам регулирующего воздействия. Такие системы относятся к нелинейным. Структурная схема системы двухпозиционного регулирования может быть представлена в виде последовательного соединения Пз-регулятора и линейные части системы, охваченных отрицательной обратной связью.
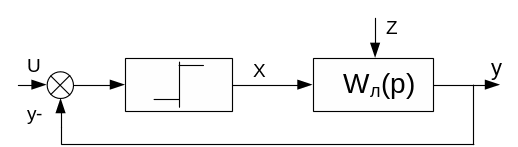
Для работоспособности системы
двухпозиционного регулирования нужно,
чтобы при равенстве передаточных функций
Wx(p) и Wz(p)
по каналам
и
текущие значения эквивалентного
возмущения объекта zэкв.
лежали бы в пределах
.
Это условие соответствует случаю, когда
основным возмущением z
является нагрузка объекта, изменение
которой компенсируется регулирующим
воздействием.
Пз-регулятор вырабатывает регулирующее воздействие, равное xmax, если текущее значение регулируемой величины у ниже ее заданного значения u, в этом случае регулируемая величина возрастает. При достижении текущим значением заданного, регулирующее воздействие х мгновенно уменьшается до хmin. Но т.к. у объект обладает инерционностью, то регулируемая величина еще продолжает возрастать в течении некоторого времени и затем понижается. При последующем пересечении регулируемой величиной заданного значения регулятор снова сформирует регулирующее воздействие xmax, что через некоторое время вновь перейдет к очередному повышению регулируемой величины. Следовательно при использовании Пз-регулятора регулируемая величина совершает колебания относительно заданного значения. Эти колебания с амплитудой А и периодом колебания T - автоколебания.
ПИД-регуляторы успешно применяются для решения многих задач управления промышленными процессами. Основная причина их широкого распространения связана с тем, что динамические свойства большинства технических процессов можно удовлетворительно аппроксиморовать динамическими моделями второго порядка. Но ПИД – регулятор не подходит для управления процессами в которых значительную роль играют следующие факторы: 1) временные задержки, 2) колебательных характер динамики системы, 3) изменения параметров, как предсказуемые, так и не предсказуемые.