Тема 17 Затухающие и вынужденные колебания

1. Найти логарифмический декремент затухания математического маятника, если за 1 минуту амплитуда уменьшилась в 2 раза. Длина маятника 1 м.

2. Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась в 2 раза. Во сколько раз она уменьшится за 3 мин? Ln2=0,69∙ e2,1=8.

3. Найти число колебаний, за время которых амплитуда колебаний уменьшится в е раз, если логарифмический декремент колебаний равен 0,01. (е – основание натуральных логарифмов).

4. За сколько секунд амплитуда затухающих колебаний уменьшится в е раз, если коэффициент затуханий равен 0,01. (е – основание натуральных логарифмов).

5. Найдите логарифмический декремент затухания, если за 200 секунд после начала колебаний амплитуда уменьшилась в е раз. (е – основание натуральных логарифмов).

6. Период вертикальных колебаний шарика на легкой пружине в воздухе равен 1 с. При погружении шарика в вязкую жидкость период колебаний уменьшился в 2 раза. Найдите по этим данным коэффициент затухания колебаний.

7. В колебательной системе под действием периодически изменяющейся внешней силы установились вынужденные колебания по закону: х=5∙ sin(π∙t + π! 3) (см.) Какова частота ( в Гц) изменения внешней силы?

8. Чему равна длина математического маятника, если через 1 минуту после начала колебаний амплитуда колебаний уменьшилась в 10 раз, а логарифмический декремент затухания равен 0,05? ln10=2,3

Найти логарифмический декремент затухания для математического маятника длиной 80 см, если через 5 минут после начала колебаний амплитуда колебаний уменьшилась в 2 раза.

10. Логарифмический декремент затухания математического маятника равен 0,003. Найдите число колебаний, за время которых амплитуда колебаний уменьшится в 2 раза. ln2=0,69

11 .Доска совершает гармонические колебания в горизонтальном направлении с периодом 5 с. Лежащее на доске тело начинает скользить, когда амплитуда колебаний достигает 0,6 м. Найдите по этим данным коэффициент трения между доской и телом.

12.3атухающие колебания совершаются по закону: х = А∙ехр(-βt)∙ cos(ωt), A = 10 см, β = 0,2 с,-1 ω= 8π∙с.-1 Найдите период колебаний, логарифмический декремент затухания и амплитуду после 10 колебаний.

13.Груз, подвешенный к невесомой пружине, растягивает ее на 10 см. Найдите период вертикальных колебаний груза на этой пружине, если логарифмический декремент затухания равен 3.

14. Определите коэффициент затухания математического маятника, если за время τ его энергия уменьшается в к раз.

Тема 18 Электромагнитные колебания

1. В контуре, состоящем из конденсатора емкости С и катушки индуктивности L, совершаются свободные незатухающие колебания, при которых амплитуда напряжения на конденсаторе равна Um . Найти связь между током I в контуре и напряжением U на конденсаторе.

2. Колебательный контур состоит из конденсатора емкости С, катушки индуктивности L с пренебрежимо малым сопротивлением и ключа. При разомкнутом ключе конденсатор разряжается до напряжения Um ,и затем в момент t=0 замкнули ключ. Найти: а) ток в контуре как функцию времени; б) ЭДС самоиндукции в катушке в моменты, когда электрическая энергия конденсатора равна энергии тока в катушке.

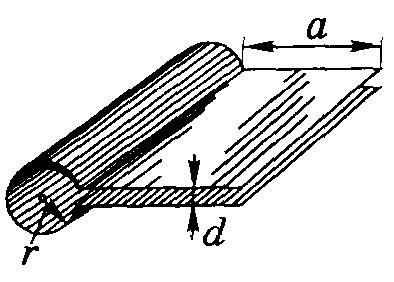
3. Найти собственную частоту ω0 резонатора, считая что его плоская часть является конденсатором, а цилиндрическая – индуктивностью. Необходимые размеры указаны на рисунке.

4. В колебательном контуре индуктивность катушки L=2,5 мГн, а емкости конденсаторов С1 = 2,0 мкФ и С2 =3,0 мкФ. Конденсаторы зарядили до напряжения U=120 B и замкнули ключ К. Найти: а) период собственных колебаний; б) амплитудное значение тока через катушку.

5. Электрическая цепь имеет пренебрежительно малое активное сопротивление. Левый конденсатор зарядили до напряжения U0 и затем в момент t=0 замкнули ключ К. Найти зависимость от времени t напряжений на обоих конденсаторах.

6. В контуре совершаются свободные затухающие колебания, при которых напряжение на конденсаторе меняется во времени по закону U=Um ∙e-βt ∙ cos(ωt). Найти моменты времени, когда модуль напряжения на конденсаторе достигает: а) амплитудных значений; б) максимальных (экстремальных) значений.

7. Контур содержит конденсатор емкости С, катушку с индуктивностью L, и активным сопротивлением R, а также ключ. При замкнутом ключе конденсатор зарядили, после чего ключ замкнули и начались колебания. Найти отношение напряжения на конденсаторе к его амплитудному значению в момент непосредственно после замыкания ключа.

8. В колебательном контуре с индуктивностью L происходят свободные затухающие колебания, при которых ток меняется во времени по закону I = Im ∙e-βt ∙sin(ωt). Найти напряжение на конденсаторе в зависимости от времени и в момент t = 0.

9. Контур состоит из конденсатора емкости С = 4,0 мкФ и катушки с индуктивностью L = 2,0 мГн и активным сопротивление R = 10 Ом. Найти отношение магнитного поля катушки к энергии электрического поля конденсатора в момент максимума тока.

10. Контур содержит две последовательно соединённые катушки с активными сопротивлениями R1 и R2 и индуктивностями L1 и L2, причем взаимная индуктивность их пренебрежительно мала. Эти катушки надо заменить так, чтобы частота и добротность контура не изменилась. Найти индуктивность и активное сопротивление такой катушки.

11. Найти время, за которое амплитуда колебаний тока в контуре с добротностью Q = 5000 уменьшилась в η = 2,0 раза, если частота колебаний ν = 2,2 МГц.

12. Колебательный контур имеет емкость С = 10 мкФ, индуктивность L=25 мГн и активное сопротивление R =1,0 Ом. Через сколько колебаний амплитуда в этом контуре уменьшится в е раз?

13. На сколько процентов отличается частота ω свободных колебаний контура с добротностью Q = 5,0 от собственной частоты ω0 колебаний этого контура?

14. Колебательный контур содержит конденсатор с утечкой. Емкость конденсатора С, его активное сопротивление R. Индуктивность катушки L. Сопротивление катушки и проводов пренебрежимо мало. Найти: а) частоту затухающих колебаний такого контура; б) его добротность.

15. Найти добротность контура с емкость С =2,0 мкФ и индуктивностью L = 5,0 мГн, если на поддержание в нем незатухающих колебаний с амплитудой напряжения на конденсаторе Um = 1,0 В необходимо подводить мощность < Р > = 0,10 мВт. Затухание колебаний в контуре достаточно мало.

16. Какую среднюю мощность должен потреблять колебательный контур с активным сопротивлением R = 0,45 Ом, чтобы в нем поддерживались незатухающие гармонические колебания с амплитудой тока I m = 30 мА? Колебательный контур содержит конденсатор емкостью С = 1,2 нФ и катушку с индуктивностью L = 6,0 мкГн и активным сопротивлением R = 0,50 Ом. Какую среднюю мощность нужно подводить к контуру, чтобы поддерживать в нем незатухающие гармонические колебания с амплитудой напряжения на конденсаторе Um = 10 В? Найти частоту затухающих колебаний контура, показанного на рисунке. Емкость С, индуктивность L и активное сопротивление R предполагаются известными.

1 7. Имеются два колебательных контура с конденсаторами одинаковой емкости. При каком соотношении между индуктивностями и активными сопротивлениями катушек частоты и затухания свободных колебаний в обоих контурах будут одинаковы? Взаимная индуктивность левого контура пренебрежимо мала.

18. Контур состоит из последовательно включенных конденсатора емкости С, катушки индуктивности L, ключа и сопротивления, равного критическому для данного контура. При разомкнутом ключе конденсатор зарядили до напряжения U0 и в момент t = 0 ключ замкнули. Найти ток I в контуре как функцию времени t. Чему равен Iмакс?

19. Катушку с активным сопротивлением R и индуктивностью L подключили в момент t = 0 к источнику напряжения U = Um∙ cos(ωt). Найти ток в катушке I (t).

20. Цепь, состоящую из последовательно соединенных конденсатора емкости С и сопротивления R, подключили к переменному напряжению U =Um ∙cos(ωt) в момент t = 0. Найти ток в цепи как функцию времени t .

21. Концы цепи, состоящей из последовательно включенных конденсатора и активного сопротивления R = 110 Oм, подключили к переменному напряжению с амплитудой Um = 110 В. При этом амплитуда установившегося тока в цепи Im = 0,50 A. Найти разность фаз между током и подаваемым напряжением.

22. На рисунке показана простейшая схема сглаживания фильтра. На вход подают напряжение U . Найти: а) выходное напряжение U’ (t); б) значение RC, при котором амплитуда переменной составляющей напряжения при выходе будет в η = 7,0 раз меньше постоянной составляющей, если ω = 314∙ с-1

23. Колебательный контур с индуктивностью L подключен последовательно к внешнему синусоидальному напряжению с амплитудой Um . Контур настроен в резонанс, при котором амплитуда установившегося тока равна Im. Найти промежуток времени τ, за который амплитуда тока уменьшится в е раз, если процесс будет происходить в режиме свободных затухающих колебаний.

24. Цепь из последовательно соединенных конденсатора емкости С = 22 мкФ и катушки с активным сопротивлением R = 20 Ом и индуктивностью L = 0,35 Гн подключена к сети переменного напряжения с амплитудой U = 180 В и частотой ω = 314 с-1. Найти: a) амплитуду тока в цепи; б) разность фаз между током и внешним напряжением; с) амплитуды напряжения на конденсаторе и катушке.

25. Цепь из последовательно соединенных конденсатора емкости С, катушки индуктивности L (без активного сопротивления) и резистора с сопротивлением R подключили к источнику гармоничного напряжения, частоту которого можно менять, не изменяя амплитуды. Найти частоту ω, при которой становится максимальным напряжение: а) на конденсаторе б) на катушке. Убедиться, что эти частоты связаны соотношениями: ω Срез < ωLрез и ωСрез· ωLрез = ω02 .

26. Переменное напряжение с частотой ω = 314 с -1 и амплитудой Um = 180 В подключено к концам цепи, состоящей из последовательно соединенных конденсатора и катушки с активным сопротивлением R = 40 Ом и индуктивностью L = 0,36 Гн. При каком значении емкости конденсатора амплитуда напряжения на катушке будет максимальной? Чему равна эта амплитуда и соответствующая амплитуда напряжения на конденсаторе?

27. Конденсатор емкости С, пространство между обкладками которого заполнено слабо проводящей средой с активным сопротивлением R, подключили к источнику переменного напряжения U = Um ∙cos(ωt). Найти установившийся ток в подводящих проводах в зависимости от времени. Сопротивление проводов пренебрежимо мало. Колебательный контур содержит конденсатор емкости С и соленоид с индуктивностью L1. Соленоид индуктивно связан с короткозамкнутой катушкой, имеющей индуктивность L2 и пренебрежимо малое активное сопротивление. Их взаимная индуктивность L12. Найти собственную частоту данного колебательного контура.

28. Найти добротность колебательного контура, в которой последовательно включен источник переменной ЭДС, если при резонансе тока напряжение на конденсаторе в n раз превышает напряжение на источнике.

29. Цепь переменного тока, состоящая из последовательно соединенных катушки и конденсатора, подключена к источнику переменной ЭДС, причем индуктивность катушки подобрана так, что ток в цепи максимален. Найти добротность системы, если известно, что при увеличении индуктивности в n раз ток в цепи уменьшается в η раз.

30. Последовательно соединенные конденсатор емкости С = 45 мкФ и катушка с активным сопротивлением подключены к источнику гармонического напряжения, частоту которого можно менять, не изменяя его амплитуды. При частотах ν1 = 1,50 кГц и ν2 = 2,50 кГц амплитуда тока оказалась одинаковой. Найти индуктивность катушки.

31. Показать, что при малом затухании добротность контура, в котором совершаются вынужденные колебания, Q ≈ ω /∆ ω , где ω0 ─ cсобственная частота колебаний, ∆ω ─ ширина резонансной кривой I (t) на высоте, в √2 раз меньшей амплитуды тока при резонансе.

32.К концам цепи, состоящей из последовательно соединенных конденсатора и катушки, подают поочередно два переменных напряжения одинаковой амплитуды, но разной частоты. Частота одного напряжения равна собственной частоте ω0, другого η в раз больше. Найти отношение амплитуд токов I0/I, возбуждаемых обоими напряжениями, если добротность системы равна Q. Вычислить это отношение для Q = 10 и 100, если η = 1,10.

33. Соленоид с индуктивностью L = 7мГн и активным сопротивлением R = 44 Ом, подключили сначала к источнику постоянного напряжения U0, а затем к генератору синусоидального напряжения с действующим значением U = U0. При какой частоте генератора мощность, потребляемая соленоидом, будет в η = 5,0 раз меньше, чем в первом случае?

34. К сети с действующим напряжением U = 100 В подключили катушку, индуктивное сопротивление которой XL = 30 Ом и импеданс Z = 50 Ом. Найти разность фаз между током и напряжением, а также тепловую мощность, выделяемую в катушке.

35. Катушка с индуктивностью L = 0,70 Гн и активным сопротивлением

R = 20 Ом, соединена последовательно с безындукционным сопротивлением R, и между концами этой цепи приложено переменное напряжение с действующим значением U = 220 В и частотой ω = 314 с-1. При каком значении сопротивления R в цепи будет выделяться максимальная тепловая мощность? Чему она равна?