Основные физические свойства жидкости

Основными физическими свойствами жидкости являются плотность, вязкость, поверхностное натяжение, удельный вес.

1) Плотность - масса жидкости приходящейся на единицу объёма

ρ = m/V, (кг/м³)

плотность несжимаемых жидкостей незначительно увеличивается с повышением давления и уменьшается с повышением температуры.

ρ _Н2О= 1000 кг/м³

ρ _возд.= 1,293 кг/м³

Плотность газовых смесей может быть определена из уравнения Менделеева-Клайперона:

ρ = m/V = PM/RT , (кг/м³)

2) Удельный вес γ - вес в единице объёма

γ = G/V , (Н/м³)

G = mg ; γ = mg/V = pg

3) Поверхностное натяжение:

на межфазовой поверхности жидкости существует тонкий слой (в несколько молекул), в которых возникает натяжение, т.к. молекулы жидкости находятся на поверхности, сильнее притягиваются молекулами внутренних слоёв, чем молекулами другой фазы на межфазной поверхности.

Действие сил поверхностного натяжения проявляются в стремлении жидкости уменьшать свою поверхность. На создание новой поверхности необходимо затратить некоторую работу.

Величина этой работы, т.е. для создания единицы поверхности при постоянной температуре, называется поверхностным натяжением:

= А/F, (Дж/м²)

4). При движении жидкостей и газов между отдельными их слоями происходит молекулярный обмен количеством движения, и возникают силы внутреннего трения.

С

dv_х/dy – называется градиентом скорости

Величина касательных напряжений внутреннего трения выражается законом Ньютона-Петрова: t = ± μ dν/dy

μ – коэффициент динамической вязкости.

войство жидкости оказывать сопротивление перемещению отдельных её слоёв вследствие существования внутренних касательных напряжений называется вязкостью.

y

dy

x

Закон Ньютона-Петрова гласит: при движении вязкой жидкости параллельными слоями действует касательное напряжение внутреннего трения, равное произведению динамического коэффициента вязкости на градиент скорости.

μ = (Н*сек/м²) = (Па*с) = Пз = 10пз = 10⁸ спз (сантипуаз)

γ = μ/ρ (м²/с) = 10⁴ ст (стокс)

У капельных жидкостей вязкость с увеличением температуры уменьшается, у упругих увеличивается.

Неньютоновские жидкости не подчиняются закону Ньютона-Петрова.

Ньютоновские жидкости: спирт, ртуть, вода, бензин.

Неньютоновские: суспензии, растворы и расплавы полимеров, коллоидные растворы, консистентные смазки.

Описывается степенными законами: τ = μ_эф.γ (dυ_x/dу)^n-1 dυ_x/dу

Основной закон гидростатики

О

На жидкость, находящуюся в неподвижном сосуде действует сила тяжести.

Выделим в жидкости элементарную площадку на глубине Z от межфазной поверхности и построим параллелепипед. Тогда на верхнюю его площадку будет действовать давление газа Р₀. Сила давления газа будет равна dP = P_o dF

На нижнюю площадку кроме того будет действовать еще и вес находящийся над площадкой dF жидкости, равной:

пределяет распределение давления в покоящейся жидкости, которая всегда действует по нормали к выделенной площадке по направлению внутрь.

P₀

Z

ddddddF

dmg = ρg dV

Общая сила, действующая на нижнюю площадку, равна:

dP = P_odF + ρg dV

Очевидно, что V столба жидкости равен:

dV = dF Z , тогда давление жидкости на глубине Z, определяется как:

р = dP/dF = P_o + ρg Z (*)

Уравнение (*) выражает основной закон гидростатики: давление в любой точке покоящейся жидкости равно сумме внешнего давления на свободной межфазной поверхности и веса столба жидкости над данной точкой. Если разделить все члены уравнения (*) на ρg - удельный вес, то получим:

ρ/ ρg = Р_о/ ρg + Z, где

Z-геометрическая высота

Р_о/ ρg – пьезометрическая высота.

Пьезометрический напор – высота столбца жидкости, которая создает в данной точке жидкости давление, равное Р. Значит, давление можно измерять в единицах высоты столбца жидкости.

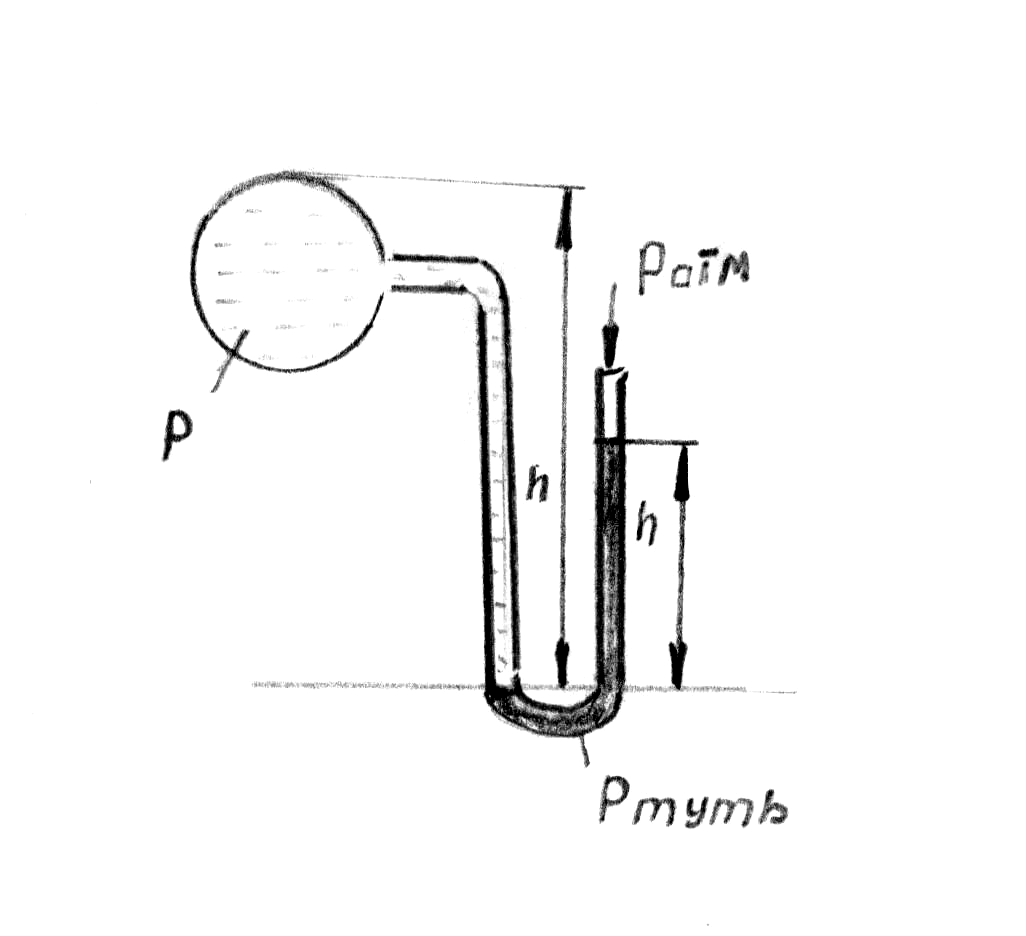
Давление в жидкостях определяется с помощью приборов, называемых манометрами.

П

Р_изб.= Р - Р_атм.

Р + ph₀g = Р_атм * p_рт hg, отсюда Р_изб = g(p_Ртh - ph₀), где

p_Рт - это плотность ртути,

p - плотность жидкости в сосуде.

Если давление на свободной поверхности жидкости Р₀ изменить на величину ΔP₀, то на основании уравнения (*), получим:

P = p₀ + pqh + Δp₀ (1)

ростейшим является U-образная трубка, заполненная ртутью.

Следовательно, на эту величину изменяется давление в любой точке покоящейся жидкости; это уравнение выражает закон Паскаля: давление на поверхность жидкости, покоящееся в состоянии равновесия, передается без изменения величины одинаково по всем направлениям.

_P2

P1 3

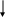
4

2

1

5

1, 2 - цилиндры;

3, 4 - поршни (плунжеры);

5 - соединительный канал.

Сила давления, действующая на малый плунжер, создает давление р в жидкости, находящейся в цилиндре 2.

Давление создается торцевой поверхностью плунжера малого диаметра:

р=Р₁/F₁,

где F₁=πd²/4 - площадь поперечного сечения плунжера

Это давление, согласно закону Паскаля, передается на трубке 5 в цилиндр 1 и действует на торец плунжера 3 с помощью поперечного сечения F₂=πD²/4.

Сила, с которой плунжер 3 действует на изделие, находится следующим образом:

Р₂ = рF₂ = P₁F₂/F₁ = P₁ *D₂²/d₂²

Таким образом, сила прессования в жидкости прямо пропорциональна отношению D²/d₂ и может достигать очень высоких значений.