
- •Раздел 1. Линейная алгебра
- •Тема 1.1. Матрицы и определители
- •1) Написание рефератов, докладов
- •2)Создание презентаций
- •Тема 1.2. Система линейных уравнений
- •1)Исследовательская работа. Решение задач
- •Раздел 2. Дифференциальное исчисление функцции
- •Основные положения теории пределов
- •7. При решении многих задач используются следующие эквивалентности, верные при X→0:
- •8. Операции над пределами функций
- •Тема 2.1. Функции, пределы, непрерывность
- •1) Написание рефератов, докладов
- •Исследовательская работа. Решение задач
- •Тема 2.2 Дифференциальное исчисление
- •1)Написание рефератов, докладов
- •2)Исследовательская работа. Решение задач
- •Тема 2.3 Применение дифференциального исчисления к исследованию функций
- •Разработка алгоритма построения графиков функций
- •?Вопросы для самопроверки
- •Раздел 3. Интегральное исчисление функции одной действительной переменной
- •1.Непосредственное интегрирование
- •2.Метод подстановки
- •3.Метод интегрирования по частям
- •Тема 3.1. Неопределенный интеграл
- •1)Исследовательская работа, решение задач
- •Тема 3.2 Определенный интеграл
- •1)Написание рефератов, докладов.
- •2)Исследовательская работа, решение задач.
- •Контрольные задачи к разделу
- •Раздел 4. Комплексные числа
- •Тема 4.1 Алгебраическая и тригонометрическая форма записи комплексных чисел
- •1) Создание презентаций
- •2) Исследовательская работа. Решение задач
- •Раздел 5. Теория вероятностей и математическая
- •Случайные события. Вероятность события
- •Теорема сложения вероятности
- •Теорема умножения вероятностей
- •Формула полной вероятности. Формула Байеса
- •Повторение испытаний. Формула Бернулли
- •Тема 5.1 Основы теории вероятностей
- •1) Исследовательская работа. Решение задач
- •Контрольные задачи к разделу
Тема 4.1 Алгебраическая и тригонометрическая форма записи комплексных чисел
1) Создание презентаций
- Показательная форма записи комплексных чисел
- История становления комплексных чисел
2) Исследовательская работа. Решение задач
Упражнения
1. Постройте радиусы - векторы, соответствующие комплексным числам:
1)z=2
3i;
2)z
=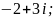 3) z =
3) z =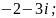 4)z =
4)z =
5)z
=2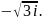
2.
Даны
числа: 1)z
=3+i;
2)
z
=3
i;
3)
z
=
3+i;
4)
z
=
3
i;
5)3;
6)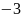 ;
7)
;
7)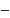 i;
8)
i.
Назовите
числа, сопряженные и противоположные
данным.
i;
8)
i.
Назовите
числа, сопряженные и противоположные
данным.
3.
На координатной плоскости дан круг с
центром в начале координат и радиусом,
равным 1 (рис.4).
Какие
числа соответствую точкам
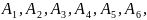 лежащим
в вершинах правильного шестиугольника,
вписанного в этот круг?
лежащим
в вершинах правильного шестиугольника,
вписанного в этот круг?
4. Дана точка, изображающая число 3+2i. Какие числа изображают точки, симметричные данной относительно: 1) действительной оси; 2)мнимой оси; 3) начала координат?
5.
Найдите
действительные числа x
и y
из условия равенства двух комплексных
чисел: 1)
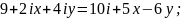 2)
2)
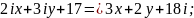 3)
3)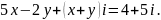
6.
Пользуясь
условием равенства двух комплексных
чисел, найдите
x
и y
из
соотношений: 1)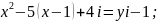 2)
2)
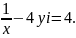
7.
Найдите
действительные значения х,
при
которых справедливо равенство
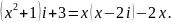
8. Найдите модуль и главное значение аргумента комплексных чисел:
1)
z
=3; 2)
z
=
;
3)
z =3i; 4)
z =
i;
5)
z
=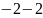 i;
6)
z =1
i;
6)
z =1 i
;
i
;
7)
z
=1
i
;
8)
z
=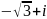 .
.
9. Чему равен аргумент: 1) чисто мнимого числа; 2) любого отрицательного числа; 3) любого положительного числа; 4)нуля?
10.
Аргумент
комплексного числа a+bi
равен
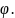 Чему равен аргумент числа a
bi?
Чему равен аргумент числа a
bi?
11.
Найдите
множество точек координатной плоскости:1)
модуль которых равен 2; 2) аргумент
которых равен

12.
Найдите все значения аргумента
комплексных чисел: 1) z
=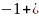 i;
i;
2)
z
=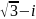 .
.
13. Вычислите:
1)
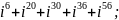 2)
2)
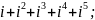
3)
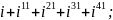 4)
4)
 ;
5)
;
5)
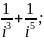 6)
6)
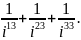
14. Выполните действия:
1)
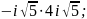 2)
2)
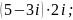 3)
3)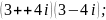
4)
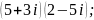 5)
5)
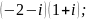 6)
6)
 7)
7)
 8)
8)
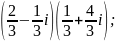
9)
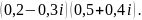
15. Выполните действия:
1)
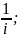 2)
2)
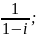 3)
3)
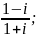 4)
4)
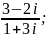 5)
5)
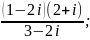
6)
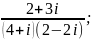 7)
7)
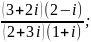 8)
8)
 9)
9)
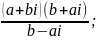
10)
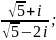 11)
11)
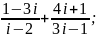 12)
12)
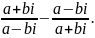
16. Представьте в тригонометрической форме комплексные числа:
1)
3i;
2)
 3) 1
3) 1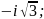 4)
4)
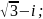 5)
5)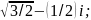 6)
6)

Контрольные задачи к разделу
4.1.1. Представить в тригонометрической форме следующие числа:
1)
2;
2) 6i;
3)
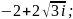 4)
4)
 5)
5)
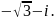
4.1.2.
Представить
в алгебраической форме числа:
1)
 2)
2)
 3)
3)
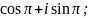 4)
4)
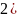 5)
5)
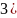
4.1.3.
Выполните
умножение, используя тригонометрическую
форму комплексного числа: 1)
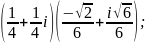 2)
3)
2)
3)
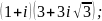 4)
4)
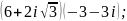 5)
5)
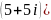 6)
6)
4.1.4.
Возведите
в степень: 1)
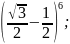 2)
2)
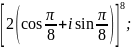 3)
3)
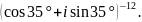
4.1.5.
Извлеките
корни: 1)
 2)
2)
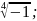 3)
3)
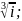 4)
4)
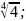 5)
5)
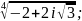 6)
6)
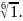
4.1.6. Выполните действия в тригонометрической и показательной формах:
1)
2)
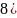
? Вопросы для самопроверки
1. Дайте определение комплексного числа.
2. Какие комплексные числа называются равными?
3. Как выглядит алгебраическая форма записи комплексного числа?
4. Действия над комплексными числами в алгебраической форме.
5. Как выглядит геометрическая форма записи комплексного числа?
6. Действия над комплексными числами в геометрической форме.
7. Дайте понятие модуля и аргумента комплексного числа.
8. Как выглядит тригонометрическая форма записи комплексного числа?
9. Действия над комплексными числами в тригонометрической форме.
10. Как выглядит показательная форма записи комплексного числа?
11. Действия над комплексными числами в показательной форме.
