4.2. Базовые алгоритмы

Рассмотрим алгоритмы, которые будут использоваться при решении практически всех задач курса. Таких алгоритмов немного, они называются базовыми. Их надо очень хорошо понять и запомнить.

Алгоритм вычисления суммы n чисел.

Задача. Вычислить сумму n чисел.

При вычислении суммы n слагаемых действие сложение повторится n раз.

Предположим, что значение каждого числа задается случайным образом, но при этом для хранения каждого очередного числа используется только одна переменная a, т.е. каждое очередное значение присваивается этой переменной. Чтобы правильно решить задачу, следует помнить о том, что оператор S:=S+A; выполняется следующим образом: вычисляется правая часть, т.е. к значению переменной S добавляется значение переменной A и полученное значение присваивается переменной S. В некоторой переменной S накапливается значение суммы, т.к. суммировать предстоит n чисел.

Перечислим действия алгоритма:

1. переменной s присвоить значение 0.

2. организовать цикл, количество повторений которого совпадает с количеством слагаемых. В цикле получить значение очередного слагаемого и добавить его к сумме.

Используя этот алгоритм, решим частную задачу: вычислить сумму первых 10 чисел натурального ряда.

Переменную, в которой предстоит накапливать сумму 10 чисел, назовем S. Операция сложения будет выполняться 10 раз.

При первом прохождении тела цикла к переменной S добавляется a = 1. Получена первая промежуточная сумма S = 1.

При втором прохождении тела цикла к переменной S (равной 1) добавляется a=2, получаем следующую промежуточную сумму S=3, при третьем проходе тела цикла к переменной S=3 добавляется a=3 и вычисляется очередная промежуточная сумма S=6.

ОБРАТИТЕ ВНИМАНИЕ: сумма постепенно накапливается.

Рассуждения будут абсолютно верны только в том случае, если начальное значение переменной S равно 0. Только тогда при первом прохождении тела цикла будет получено значение переменной S равное первому слагаемому.

На рис. 4.2. представлен алгоритм нахождения суммы первых 10 членов натурального ряда.

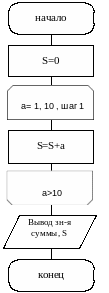
Рис. 4.2. Схема алгоритма вычисления суммы первых 10 членов натурального ряда.

Запишем текст программы.

PROGRAM SUMMA;

USES CRT;

VAR

a, S: integer;

BEGIN

clrscr;

S:=0;

FOR a:=1 TO 10 DO

S := S + a;

writeln('сумма = ',S);

writeln('Нажмите любую клавишу для выхода...');

readln;

END.

Выполним трассировку алгоритма.

I прохождение цикла		II прохождение цикла		III прохождение цикла
a=1, S=0 S:=S+a (1=0+1) a=1+1 (шаг изменения) a<=10? Да		a=2, S=1 S=S+a (3=1+2) a=2+1 a<=10? да		a=3, S=3 S=S+a (6=3+3) a=3+1 a<=10? да (и т.д.)
X прохождение Цикла
a =10, S=45 S=S+a (55=45+10) a=10+1 a<=10? Нет		выход из цикла a=10, S=55

Пример 1. Вычислить сумму 12 целых чисел, введенных с клавиатуры. Алгоритм суммирования не изменяется. Изменился способ задания значений слагаемых. Для ввода чисел с клавиатуры используется процедура - оператор readln(a), который останавливает выполнение программы и ждет, пока пользователь введет с клавиатуры данные и нажмет Enter. Данные, введенные с клавиатуры, будут занесены в переменную a. Процедура - оператор Readln будет рассмотрен более подробно далее, а сейчас нужно лишь понимать для чего он служит.

PROGRAM SUMMA_2;

USES CRT;

VAR

a: integer; {введенное число}

i: integer; {счетчик цикла}

S: integer; {сумма}

BEGIN

clrscr;

S:=0;

FOR I:=1 TO 12 DO

BEGIN

write('задайте значение очередного слагаемого: ');

readln(a);

S:=S+a

END;

writeln('Сумма = ', S);

writeln('Нажмите любую клавишу для выхода...');

readln;

END.

Пример 2. Вычислить сумму натуральных чисел от 100 до 300.

PROGRAM SUMMA_3;

USES CRT;

VAR

a: integer;

S: integer;

BEGIN

clrscr;

S:=0;

FOR a:=100 TO 300 DO

S:=S+a;

writeln('сумма = ', S);

writeln('Нажмите любую клавишу для выхода...');

readln;

END.

Подсчет количества чисел, удовлетворяющих заданному условию.

Задача. Подсчитать количество отрицательных чисел, введенных с клавиатуры (количество чисел равно 10).

Необходимые действия:

Ввести переменную (счётчик), задать начальное значение счётчика равным нулю.

Организовать цикл, количество повторений которого равно количеству введённых чисел.

Каждое введенное число проверять на знак, в том случае, если число отрицательное, увеличивать счётчик на единицу.

Выйдя из цикла проверить значение счётчика. Если счётчик равен нулю, следовательно отрицательные числа в вводимой последовательности отсутствовали, иначе выводим на экран значение счётчика.

На рисунке 4.3 представлен алгоритм решения задачи.

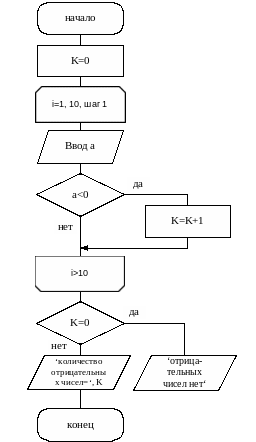
Рис. 4.3. Схема алгоритма вывода отрицательных чисел.

Текст программы

PROGRAM N;

USES CRT;

VAR

a: integer; {входная переменная}

K: integer; {счетчик отрицательных чисел}

i: integer; {счетчик цикла}

BEGIN

clrscr;

K:=0;

FOR i:=1 TO 10 DO

BEGIN

write('Задайте значение переменной a: ');

readln(a);

IF a<0 THEN

K:=K+1

END;

IF K=0 THEN

writeln('отрицательных чисел нет')

ELSE

writeln('количество отрицательных чисел ', K);

writeln('Нажмите любую клавишу для выхода...');

readln;

END.

Пример. С клавиатуры последовательно вводятся целые числа. Вычислить сумму чисел, кратных трём.

Текст программы.

PROGRAM NN;

USES CRT;

VAR

a, K, S, i: integer;

BEGIN

clrscr;

K:=0;

S:=0;

FOR i:=1 TO 10 DO

BEGIN

write('задайте значение переменной a: ');

readln(a);

IF a mod 3 = 0 THEN

BEGIN

K:=K+1;

S:=S+a

END;

END;

IF K=0 THEN

writeln('чисел кратных 3 нет.')

ELSE

writeln('сумма чисел кратных 3 = ', S);

writeln('Нажмите любую клавишу для выхода...');

readln;

END.

Обратите внимание: кроме переменной S вводится переменная К, которая служит счётчиком для подсчёта чисел кратных трём. Если счётчик остался равным нулю, это означает, что в последовательности не было чисел, кратных трём.

Алгоритм вычисления n!.

Напомним, что .

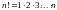Принято считать: что 0!=1.

Алгоритм вычисления 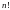практически не отличается от алгоритма вычисления суммы, действие сложения заменяется действием умножения, а начальное значение переменной, в которой будет накапливаться произведение, естественно, равно 1.

Текст программы.

PROGRAM FACT;

USES CRT;

VAR

F, i: integer;

BEGIN

clrscr;

F:=1;

FOR i:=1 TO 5 DO

F := F * i;

writeln('Факториал 5 (5!) = ', F);

writeln('Нажмите любую клавишу для выхода...');

readln;

END.

Алгоритм вычисления aⁿ.

Алгоритм вычисления 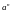, где n — натуральное число. 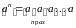, т.е. это произведение n одинаковых сомножителей.

Следовательно, используем предыдущий алгоритм, внеся необходимые коррективы.

PROGRAM DEGREE;

USES CRT;

VAR

a: integer; {основание}

n: integer; {показатель степени}

W: integer; {результат }

i: byte; {счетчик цикла}

BEGIN

clrscr;

write('ведите число: ');

readln(a);

write('введите степень: ');

readln(n);

W:=1;

FOR i:=1 TO n DO

W := W * a;

writeln(a,' в степени ', n, ' равно ', W);

writeln('Нажмите любую клавишу для выхода...');

readln;

END.

Примеры.

1. Вычислить:

...

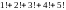
S:=0; { переменная для накопления суммы }

F:=1; { переменная для накопления }

FOR I:=1 TO 5 DO

BEGIN

F:=F*I; {используем два базовых алгоритма}

S:=S+F {вычисления n! и вычисления суммы}

END;

2. Вычислить: a(a-1)(a-2)...(a-(n-1)), где a - действительное число.

...

readln(a);

p:=1;

for i:=1 to n do

p:=p*(a*(i-1));

Итак, достаточно подробно рассмотрена конструкция цикла со счетчиком, а также примеры использования этой конструкции. При использовании конструкции цикла со счетчиком необходимо помнить о том, что число повторений цикла известно к началу его выполнения. Однако часто число повторений тела цикла неизвестно заранее и определится в процессе реализации циклического алгоритма.