Глава 3. Реализация алгоритмов ветвления
3.1. Условный оператор
В разветвляющихся вычислительных процессах (алгоритм ветвления) отдельные этапы вычислений выполняются не всегда в одном и том же порядке, а в зависимости от некоторых условий выбираются для исполнения различные их последовательности.
Рассмотрим сказанное выше на конкретном примере.
Требуется вычислить
корни квадратного уравнения вида
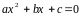
Перечислим последовательность действий для решения:
задать коэффициенты a, b, c,
вычислить значение дискриминанта,
проверить значения дискриминанта и, в зависимости от полученного ответа, выполнить то или иное действие.
В пункте 3 алгоритма проводится анализ значения дискриминанта, а затем выбор действия, в зависимости от значений дискриминанта, т.е. данный алгоритм относится к алгоритмам ветвления.
На рисунке 3.1. представлена схема решения задачи (текст программы написать самостоятельно после изучения следующего параграфа).
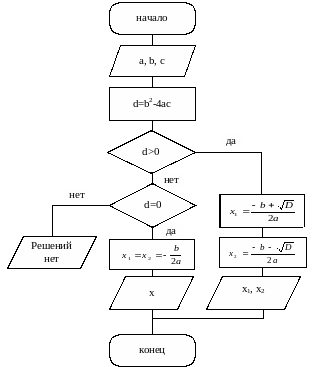
Рис. 3.1. Схема алгоритма нахождения корней квадратного уравнеия.
Для реализации такого типа алгоритма, необходим оператор, который «выберет» то или иное действие (или группу действий) в зависимости от истинности или ложности условия выбора. Такой оператор называется оператором уловного перехода (т.е. перейти к тому или иному действию по значению условия). Есть несколько возможных вариантов записи оператора условного перехода.
Полная форма оператора
IF <условие> THEN <оператор1>
если тогда
ELSE <оператор2>
иначе
Пример.
Из двух чисел a и b вывести на экран значение большего числа.
IF a > b THEN
writeln(‘ большее число а’, a)
ELSE
writeln(‘ большее число b’, b);
Обратите внимание на запись служебных слов и операторов. Каждое слово ELSE пишется под своим словом IF.
ВНИМАНИЕ: перед словом ELSE нельзя ставить точку с запятой.
Краткая форма оператора.
Допускается опускать служебное слово ELSE. Оператор в этом случае выглядит следующем образом
IF <условие> THEN <оператор1>;
Как работает эта конструкция?
Запишем конструкцию оператора еще раз:
IF <условие> THEN <оператор1>;
<оператор2>;
<оператор3>;
...
Возможны два варианта:
условие истинно, в этом случае программа «уходит в сторону» на оператор 1, он выполняется, а затем продолжает выполнять последовательности операторов: оператор 2, оператор 3 и т. д.
условие ложно, оператор 1 НЕ выполняется, следовательно, сразу выполняется следующий по порядку оператор: оператор 2, затем оператор 3 и т. д.
Пример.
Вычислить значение
функции,
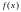
в
зависимости от значения аргумента x
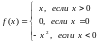
Решение этой задачи можно записать следующим образом:
IF x<0 THEN
y=x;
IF x=0 THEN
y=0;
IF x<0 THEN
y=-x*х;
Решая всевозможные задачи, можно убедиться, что очень часто необходимо выполнять группу операторов либо за словом «then» (т.е. по истинности условия), либо за словом else (при ложности условия), либо и в том и другом случае.
Для того чтобы записать группу действий необходимо использовать составной оператор begin end (операторные скобки).
IF <условие> THEN BEGIN
оператор 1;
оператор 2;
...
оператор n;
END
ELSE
оператор;
IF <условие> THEN оператор
ELSE BEGIN
оператор 1;
оператор 2;
...
оператор n;
END;
IF <условие> THEN BEGIN
оператор 1;
оператор 2;
...
оператор n;
END
ELSE BEGIN
оператор 1;
оператор 2;
...
оператор n;
END;
Обратите внимание на синтаксис: между словами BEGIN и END стоят операторы, следуя правилу языка Турбо Паскаль, они отделены точкой с запятой.
Перед словом ELSE точки с запятой не может быть, это один оператор, состоящий из слов IF...THEN...ELSE.
Вложенные операторы IF.
Пример.
Определить, попадает ли число X в интервал от -2 до 13.
Необходимо проверить два условия: 1) X должно быть больше -2, если это условие является истиной, то проверяем второе условие, X должно быть меньше 13, в том случае, когда оба условия истинны, можно сказать, что данное значение X является решением.
Как это записать?
{проверяем 1-е условие}
IF X > -2 THEN
{проверяем второе условие }
IF X < 13 THEN
writeln(‘X удовлетворяет условию’)
ELSE
writeln(‘X>=13’)
ELSE
writeln(‘X<= -2’);
Вложенность операторов IF неограниченна.
Составные условия.
Задача. Определить, попадает ли точка X в интервал (-3, 10). Решение можно записать с помощью вложенного оператора IF:
IF X > -3 THEN
IF X < 10 THEN
writeln(‘точка попадает в интервал’);
Условие попадания числа X в интервал звучит так: «если X больше -3 И X меньше 10, тогда число X попадает в интервал». Две операции отношения соединили союзом «и», графически принадлежность интервалу изобразим следующим образом
В качестве условия в операторе условного перехода используются только простые условия — т.е. отношения равенства, либо неравенства. В языке Турбо Паскаль из простых условий разрешается строить составные, более сложные условия, состоящие из нескольких простых условий связанных некоторыми логическими операциями, каждое простое условие заключается в скобки.
Простые условия могут соединяться союзами AND, OR и отрицанием NOT, операцией XOR.
Составные условия также как и простые используются в условных операторах и в операторах цикла с предварительной и последующей проверкой условия. Например, для того, чтобы проверить входит ли число x в интервал [a,b] можно использовать составное условие:
IF (X >= a) AND (X <= b) THEN оператор