МАТЕМАТИКА (ТЕОРИЯ)

Профиль – начальное образование) Пояснительная записка

Данный УМК разработан для студентов – заочников направления «Педагогическое образование» по профилю «Начальное образование». По учебному плану на изучение «Математики» выделено всего 14 аудиторных часов, в течение которых преподавателю необходимо ознакомить студентов с теоретическими основами курса математики начального образования.

Запланированных 4 часов лекционных занятий достаточно только для краткого ознакомления с задачами изучения курса, рекомендации списка учебной литературы.

Анализ многих программ по математике, предлагаемых для изучения учащимся начальной школы, показывает, что учитель, работающий в школе или готовится к этой работе, должен иметь как достаточно серьезную теоретическую подготовку, так и обладать развитым математическим и логическим мышлением. В связи с этим в подготовку бакалавра – будущего учителя начального образования – целесообразно включить не только изучение фактического содержания курса математики начального образования (множеств, натуральных чисел, делимости чисел, систем счисления, простейших понятий функции и уравнения), но и некоторые сведения методологического характера - элементов математической логики, методов определения математического понятия, аксиоматического метода построения теории и др.

В дополнение к существующей учебной литературе для подготовки учителя начального образования по математике автор разработанного УМК предлагает необходимый, на его взгляд, теоретический материал по дисциплине «Математика».

Предложенный курс разбит на темы, в процессе изложения содержания тем выделены отдельные пункты, не предполагается никаких почасовых ограничений, материал предназначен в основном, для самостоятельного изучения курса математики.

Тема I - множества

1. Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой

2. Операции с числовыми множествами (объединение, пересечение, разность).

3. Декартово произведение множеств

1. Понятие множества, геометрическая интерпретация числовых множеств на числовой прямой

Множество – основное понятие, оно не определяется, вводится на примерах: множество жителей города - конечное, множество натуральных чисел N={1;2;3;…n…}-бесконечное. Каждое множество состоит из элементов: a;b;c;…m;1;2;3;…n…; элемент а принадлежит множеству А ( ); если В={x| }, то -пустое. Множества чисел, расположенных между двумя данными числами, иллюстрируются числовой прямой (прямой линией с началом координат (точкой О)), направлениями и масштабом: множество действительных чисел R= ; отрезок - _{(см.рис.1);}

Рис.1

интервал – (a;b)={x|a<x<b}; полуинтервалы - и ; лучи - и ; открытые лучи - и . На рисунке 2:числа натурального ряда (1), полуинтервал [-2;0) (2); луч (- (3); луч [-1; (4) (см. рис 2)

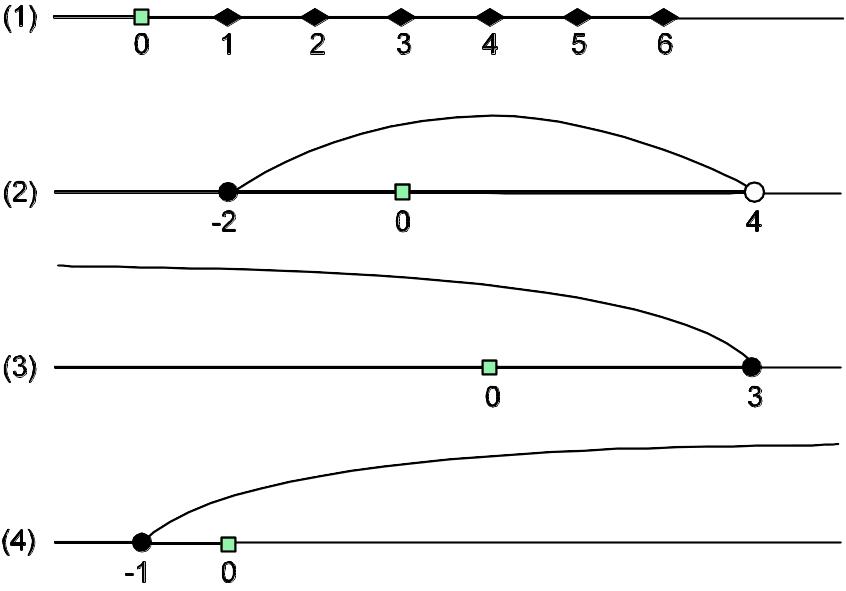
Рис.2

Для множеств А={2;4;6;8} и B={4;6} имеем: все элементы В являются элементами множества А; множество В –это подмножество (правильная часть) множества А.

Опр. Множество В называется подмножеством множества А, если каждый элемент множества В принадлежит множеству А. Например: ;

_{Пример 1. (а) , тогда ; (b). , тогда .}

Связь множества и его подмножества –это отношение включения, для него выполняются свойства: [1]. - рефлексивности; [2]. Из и следует - транзитивности; [3]. . Отношение можно проиллюстрировать рисунком, где каждое множество изображается в виде овала; это диаграммы (круги) Эйлера – Венна (см. рис.3).

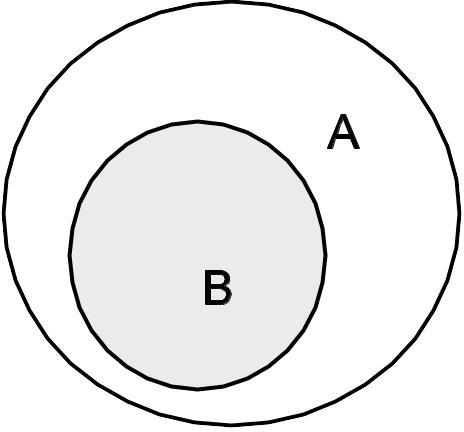
Рис.3

Если для множеств для А и В выполняется и , то А и В состоят из одних и тех же элементов: ; А и В связаны отношением равенства.

Опр.1. Равными множествами называются множества, которые состоят из одних и тех же элементов.

Пример 2. _{, .}

Для отношения равенства выполняются свойства: [4]. А= А – свойство рефлексивности; [5]. Из А=В следует В=А –свойство симметричности; [6]. Из А=В и В=С следует А=С – свойство транзитивности. .