Метод взвешенных конечных разностей.

Этот метод состоит в том, что величина влияния каждого фактора определяется как по первому, так и по второму порядку подстановки, затем результат суммируется и от полученной суммы берется средняя величина, дающая единый ответ о значении влияния фактора. Если в расчете участвует больше факторов, то их значения рассчитываются по всем возможным подстановкам.

Опишем этот метод математически, используя вышепринятые обозначения

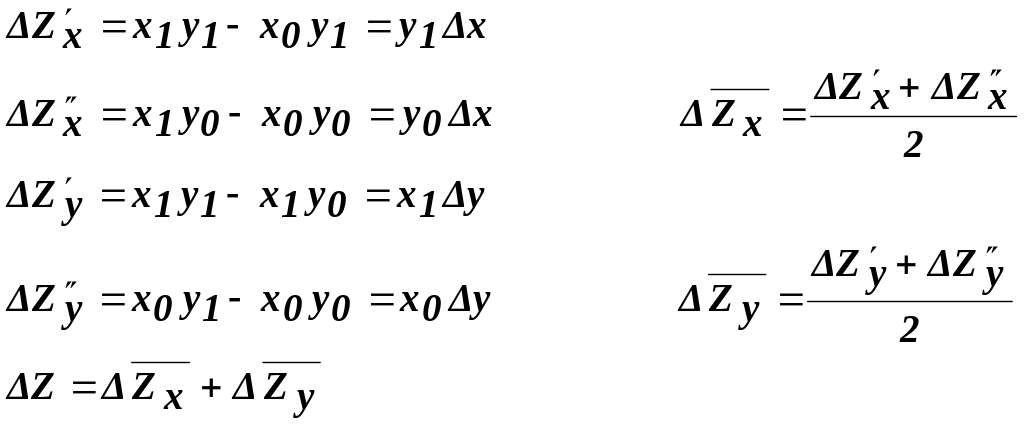
Метод весьма трудоемкий и в своей основе (только для двухфакторной мультипликативной модели) идентичен методу простого прибавления неразложимого остатка.

Логарифмический метод.

Этот метод состоит в том, что происходит логарифмически пропорциональное распределение остатка по двум факторам. В этом случае не требуется установления очередности действия факторов.

Математически метод описывается следующим образом.

Факторную систему z=xy можно представить в виде lg z=lg x + lg y , тогда можно записать

lg z₁ - lg z₀ = (lg x₁ - lg x₀)+( lg y₁ - lg y₀)

или

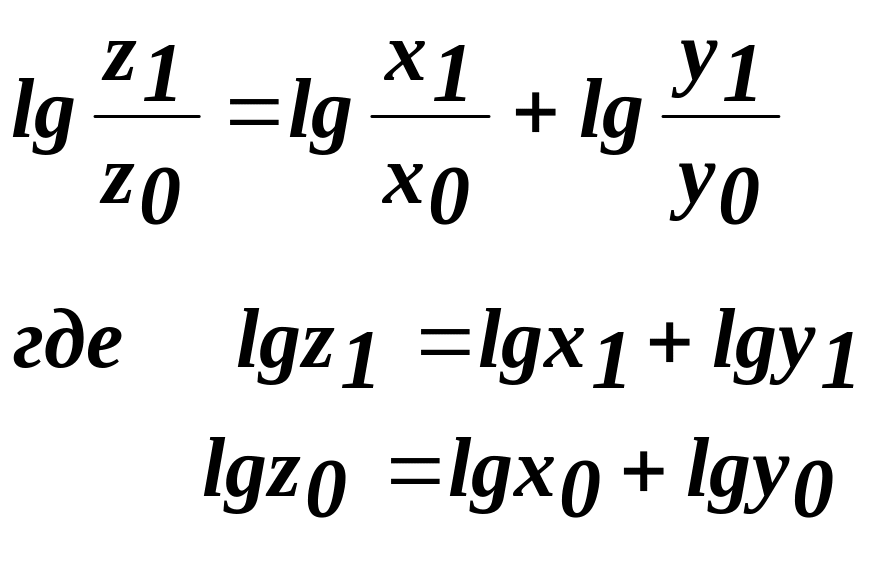
Разделив обе части формулы на lg (z₁/z₀) и умножив на ΔZ получим:

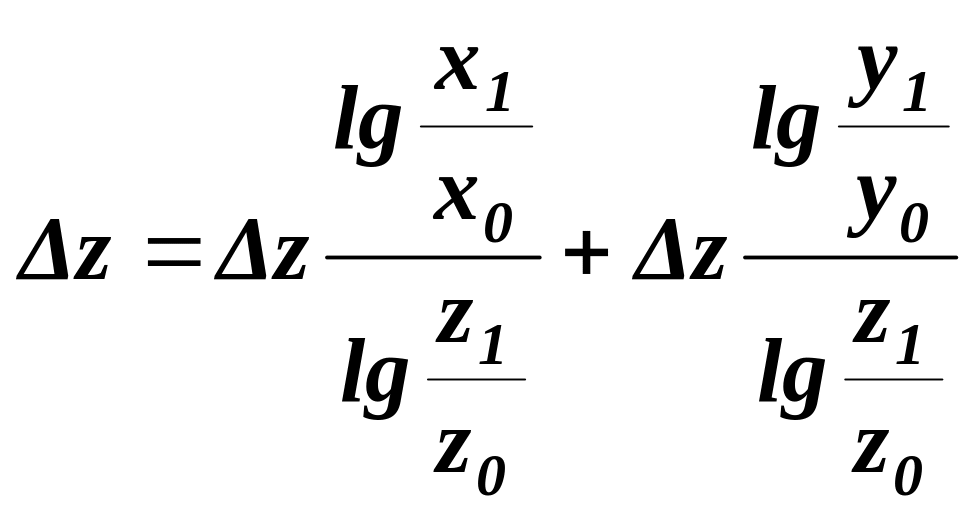
или

(1)

где

Выражение (1) для Z представляет собой логарифмическое пропорциональное распределение по двум искомым факторам. Метод позволяет определить безостаточное влияние не только двух, но и многих факторов на изменение результативного показателя, не требуя установления очередности действия.

Формулу (1) для z можно записать иначе:

(2)

где

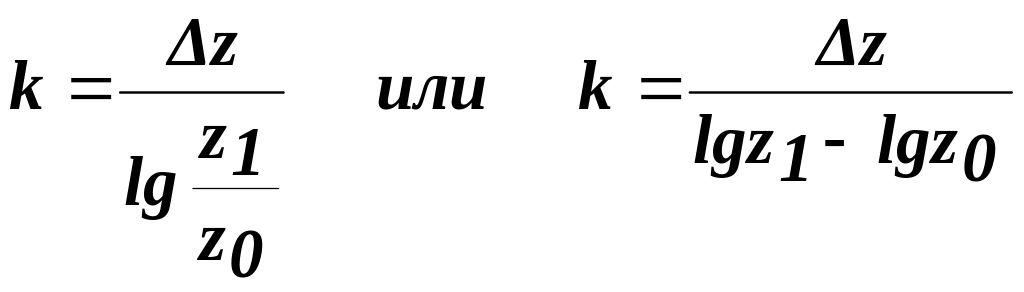
Например, для мультипликативной модели вида z=xypm суммарное приращение результативного показателя z составит:

Данная формула в случае взаимного погашения факторов не позволяет использовать указанный метод. Поэтому формула (1) в настоящее время используется как классическая, описывающая логарифмический метод анализа. При этом не имеет значения, какой логарифм используется (натуральный ln или десятичный lg).

Основной недостаток логарифмического метода - он не может быть «универсальным», его нельзя применять при анализе любого вида моделей факторных систем. Однако, иногда возможно перейти от анализа кратных моделей факторных систем к мультипликативным, что дает возможность применить указанный метод.

3. Методы комплексной оценки хозяйственно-финансовой деятельности.

Комплексная оценка хозяйственной деятельности - это ее характеристика, полученная в результате одновременного и согласованного изучения совокупности показателей, отражающих все (или многие) аспекты хозяйственных процессов, и содержащая обобщающие выводы о результатах деятельности объекта на основе выявления качественных и количественных отличий от базы сравнения (плана, нормативов, предшествующих периодов и т.д.).

Теоретически следует, что оценивать достижения предприятий надо по одному какому-либо показателю. Однако сложность производственно-хозяйственной деятельности не позволяет выделить из числа обобщающих показателей какой-либо один в качестве основного.

Для получения обобщающих комплексных оценок можно применять различные методы сведения показателей в единый интегральный .

В настоящее время используются следующие методы построения интегрального показателя:

1. Метод сумм.

Интегральный показатель комплексной оценки получается суммированием фактических значений, или же рассчитывается для каждого производственного объекта по формуле

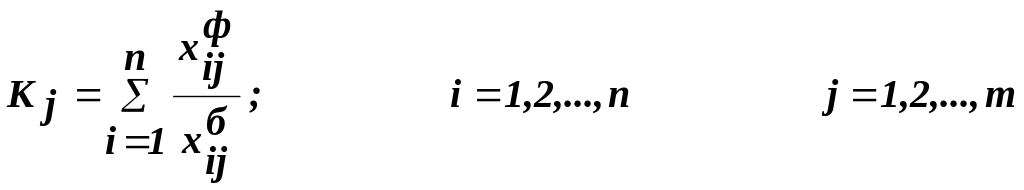
или

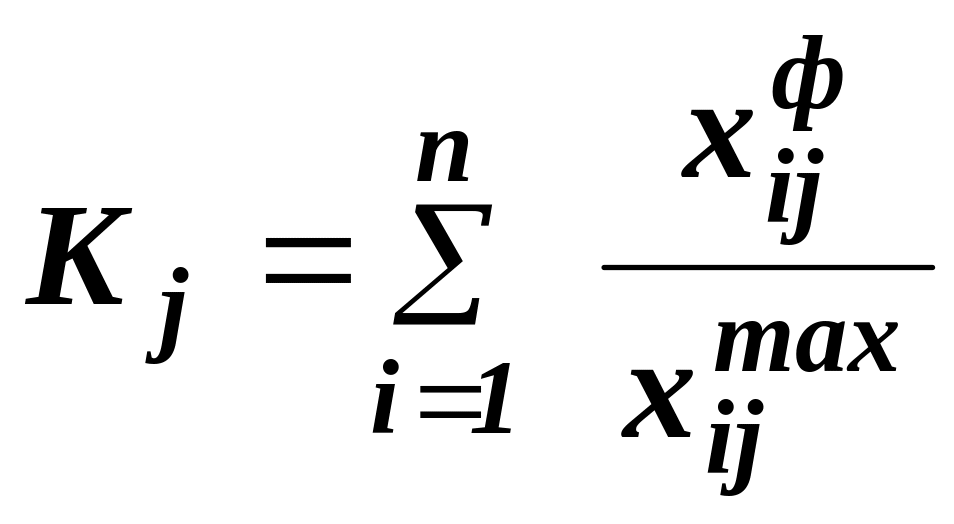
где х^ф_ij, х^б_ij, x^max_ij- соответственно фактическое, базисное и максимальное (эталонное) значения i-го показателя на j-м производственном объекте.

Результаты, основанные на расчете комплексной оценки по методу сумм с простым суммированием, приведены в табл. 1.

Таблица 1. Оценочные результаты, полученные методом сумм

Номер	Значение показателей			К	Полученные
цеха	1	2	3		места
1	98,0	100,0	101,0	299,0	2
2	101,4	101,6	102,2	305,2	1
3	100,6	100,1	98,0	298,7	3

Недостатком метода является возможность высокой оценки результатов по интегральному показателю при значительном отставании по какому-либо частному показателю, которое покрывается за счет высоких достижении по другим частным показателям.

2. Метод геометрической средней предполагает расчет коэффициентов для оцениваемых показателей, таких чтобы 0a_ij1. За единицу принимается значение, соответствующее наиболее высокому уровню данного показателя.

Обобщающая оценка получается в виде коэффициента:

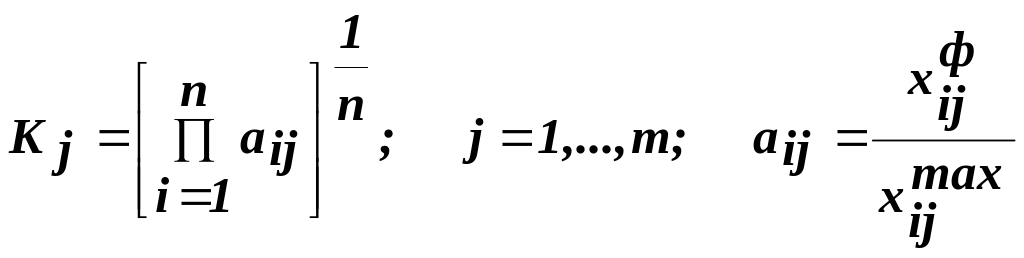
Этот метод целесообразно применять при относительно малом числе показателей и в случае, если большинство их значений близко к единице.

В некоторых случаях применим метод коэффициентов, когда оценка получается умножением соответствующих коэффициентов:

Этот метод практически не отличается от метода средней геометрической.

3. Метод суммы мест предполагает предварительное ранжирование объектов по отдельным показателям. Каждому показателю соответствует новый параметр S_ij, определяющий место каждого объекта среди других по i-му показателю.

Составляется таблица баллов {S_ij} и на основе этой матрицы рассчитывается конкретное значение обобщающей оценки:

Применение методов сумм, суммы мест, геометрической средней возможно только в случае однонаправленности влияния всех оцениваемых параметров на эффективность. Однонаправленность частных показателей позволяет ранжировать производственные объекты по возрастанию (убыванию) значений интегрального показателя. В случае разнонаправленности показателей, при расчете показателя комплексной оценки следует рассматривать обратные к исходным величинам показатели. Результаты расчета с помощью метода суммы мест представлены в табл. 2.

Таблица 2. Места, полученные методом суммы мест.

Номер цеха	Значение показателей			Кj	Полученные места	Полученные места с учетом сравнительной значимости aij
	1	2	3
1	3	2,5	2	7,5	1	1
2	1	1	3	5	3	2
3	2	2,5	1	5,5	2	3

4. Метод расстояний.

Его основой является учет близости объектов по сравниваемым показателям к объекту-эталону. За эталон может быть принят условный объект с максимальными элементами по всем показателям

x_i,m+1=max_j (x_ij); i=1,2,...,n; j=1,2,...,m

Расчет комплексной оценки проводится по формуле евклидового расстояния. Перед конкретными расчетами проводится нормирование путем деления значений показателей x_ij на значения показателя эталонного объекта x_i,m+1. Для каждого объекта рассчитывается расстояние до эталона по следующей формуле:

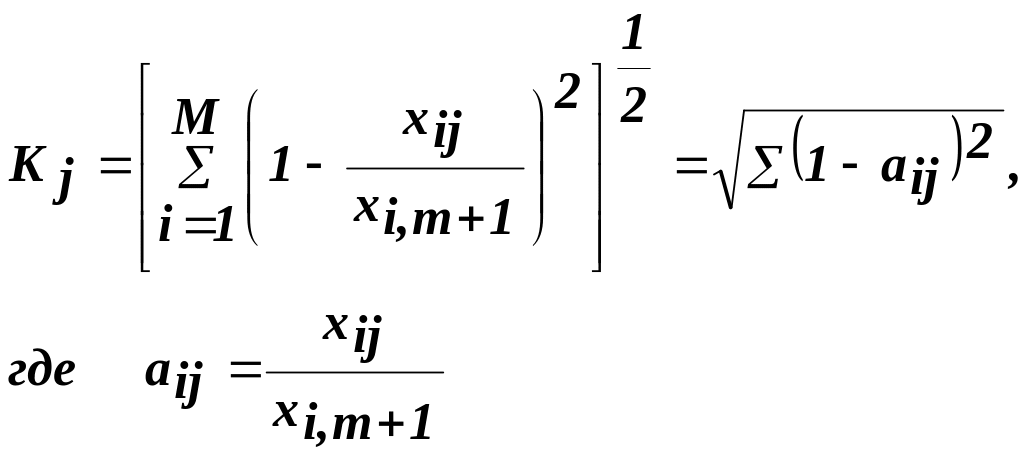
где k_j - рейтинговая оценка для j-го предприятия (объекта).

Упорядочивая значения k_j по возрастанию, получаем комплексное ранжирование объектов, причем наименее удаленный от точки эталона объект получает наивысшую оценку (первое место). Чем меньше k_j тем лучше.